Теоретическая механика — курс лекций с примерами и образцами решения, основными формулами и законами

Оглавление:

Здравствуйте, на этой странице я собрала полный курс лекций по предмету «теоретическая механика», кстати студенты обычно называют этот предмет «теормех» или «термех» .

Лекции подготовлены для студентов любых специальностей и охватывает полный курс предмета « теоретическая механика ».

В лекциях вы найдёте основные законы, теоремы, формулы и примеры задач с подробным решением.

Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Теорети́ческая меха́ника (в обиходе — теормех, реже — термех) — наука об общих законах механического движения и взаимодействия материальных тел. Будучи по существу одним из разделов физики, теоретическая механика, вобрав в себя фундаментальную основу в виде аксиоматики, выделилась в самостоятельную науку и получила широкое развитие благодаря своим обширным и важным приложениям в естествознании и технике, одной из основ которой она является. На основных законах и принципах теоретической механики базируются многие общеинженерные дисциплины, такие, как сопротивление материалов, строительная механика, гидравлика, теория механизмов и машин, детали машин и другие. На основе теорем и принципов теоретической механики решаются многие инженерные задачи и осуществляется проектирование новых машин, конструкций и сооружений. wikipedia.org/wiki/Теоретическая_механика

Кинематика

Как самостоятельный раздел механики кинематика оформилась сравнительно недавно. Важность геометрического изучения движения отмечал еще Ж. Даламбер (1717—1783), но лить А. Ампер (1775—1836) обосновал необходимость изучения геометрических свойств движения. В 1838 г. французский математик и инженер Ж. Понселе (1788—1867) представил факультету наук в Париже свой первый курс кинематики.

Дальнейшее развитие основ кинематики связано с именами М. Шаля (1793—1880) и Л. Эйлера (1707—1783). В 1862 г. французским механиком А. Резалем (1828—1896) создан курс «Чистой кинематики», в котором приводятся и аналитические методы изучения движения. С появлением этого курса кинематика окончательно утвердилась как самостоятельный раздел механики.

Кинематика изучает движения материальных тел, не останавливаясь на причинах, вызывающих эти движения. По своему содержанию она является геометрией движущихся материальных объектов, в которой независимой переменной является время. Всякое движение материального тела или состояние его покоя можно представить лишь но отношению к каким-то другим телам. Поэтому всякое движение имеет относительный характер. Конкретное представление о движении зависит от того, в какой системе мы это движение рассматриваем.

Геометрическое пространство, но отношению к которому изучается движение материальных тел, определим системой декартовых осей. Движение происходит во времени. Будем предполагать, что возможна такая арифметизация течения времени, при которой одновременность каких-либо событий не зависит ни от природы и места самих событий, ни от выбора системы отсчета, относительно которой наблюдаются события. Определенное таким образом время будем называть абсолютным. Более детальное рассмотрение вопросов, связанных с определением пространства и времени, отнесем к разделу «динамика».

Лекции:

Кинематика абсолютно твердого тела

Определения. Абсолютно твердым телом называют такую систему материальных точек, расстояния между двумя любыми точками которой остаются всегда неизменными. Абсолютно твердое тело либо заполняет некоторую область пространства, либо состоит из нескольких отдельных точек. Перемещения абсолютно твердого тела в пространстве могут быть либо свободными, либо стесненными некоторыми условиями. Так, например, перемещения твердого тела будут стеснены, если одну из его точек сделать неподвижной. Если закрепить две точки твердого тела, то возможными движениями такого тела будут только вращения вокруг неподвижной прямой, проходящей через эти закрепленные точки. Такую прямую называют осью вращения твердого тела. Если закрепить еще одну точку твердого тела, не расположенную на оси вращения, то тело не сможет перемещаться и будет оставаться неподвижным. Таким образом, три точки твердого тела, не расположенные на одной прямой, полностью определяют положение твердого тела. Для определения движения твердого тела достаточно знать закон движения трех его точек, не расположенных на одной прямой.

Лекции:

Ускорение точки в сложном движении

Теорема Кориолиса. Между ускорениями точки в подвижной и неподвижной системах отсчета существует более сложная
зависимость, чем между скоростями. Эта зависимость впервые
была установлена французским механиком Г. Кориолисом A792—1843) при аналитическом изучении движения материальной точки.
Чтобы выяснить эту зависимость, рассмотрим движение материальной точки М в подвижной системе 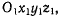теоретическая механика которая в свою
очередь совершает некоторое движение относительно неподвижной
системы отсчета Oxyz (например, материальная точка перемещается
по твердому телу, которое само движется относительно
неподвижной системы координат).

Лекции:

Распределение ускорений в плоскопараллельном движении твердого тела

Плоскопараллельное движение является частным случаем движения твердого тела. На практике этот случай встречается наиболее часто, а потому и будет исследован особо. При изучении плоскопараллельного движения твердого тела, как это уже отмечалось выше, можно ограничиться рассмотрением движения некоторого плоского сечения твердого тела.

Лекции:

Кинематические уравнения Эйлера

При изучении движения твердого тела, у которого закреплена одна точка, положение такого тела удобно определять специальными углами, называемыми углами Эйлера.

Лекции:

Статика

Геометрическая статика

Статикой называется часть механики, изучающая условия, которым должны удовлетворять силы, действующие на систему материальных точек, при которых система находится в равновесии, а также условия эквивалентности системы сил.

Разновесие, как и движение, можно изучать только по отношению к некоторой определенной системе координат, принимаемой за неподвижную, или за абсолютную. В дальнейшем будем вводить некоторые идеальные модели материальных тел, упрощающие изучение последних. В наиболее простых задачах будем рассматривать равновесия и движения таких материальных тел, положения которых с достаточной точностью могут быть определены как положения материальных точек, размерами которых можно пренебрегать при изучении движения или равновесия этих тел. Такие материальные тела будем называть материальными точками. Материальные точки могут быть представлены как результат деления физического тела на бесконечно большое число частей. Но они могут представлять и конечные тела, обладающие определенным количеством вещества, когда размеры этих тел становятся несущественными. Второй из наиболее важных моделей является модель абсолютно твердоготела. Абсолютно твердым телом называют такую совокупность материальных точек, расстояния между которыми не могут быть изменены никакими действиями. Реальные тела обычно могут изменять свою форму, при этом изменяются и расстояния между отдельными точками тел. Однако в ряде случаев эти изменения (деформации) настолько малы, что ими можно пренебрегать.

Одним из основных понятий механики является понятие силы. Силами в механике называют объективные причины, являющиеся результатом взаимодействия материальных объектов, способные вызвать движение материальных тел из состояния покоя или изменить

существующее движение последних. Равными силами называются такие, которые вызывают одинаковые движения одного и того же объекта. Так как всякое движение материальных тел имеет относительный характер, а сила определяется вызываемым сю движением, то и понятие силы должно иметь относительный характер. Одно и то же тело в различных системах отсчета в одно и то же время оказывается подверженным действию различных сил, зависящих от относительного движения систем отсчета. Мы не будем здесь заниматься вопросами происхождения сил, относя эти вопросы к курсам физики

Мы будем говорить, что несколько сил, действующих на материальную точку, находятся в равновесии, если, будучи приложенными к этой точке, они не сообщают ей никакого движения относительно данной системы координат, и ускорение точки в этой системе остается равным нулю. Система материальных точек находится в равновесии, если она не получает никакого движения из состояния покоя от сил, действующих на эту систему.

Из повседневного опыта известно, что силы, действующие на твердое тело, имеют векторный характер. Они имеют определенную величину, направление и линию действия, а также точку приложения. Если точка приложения силы совпадает с центром тяжести тела, то последнее под действием силы начинает двигаться из состояния покоя поступательно и при изучении такого движения тела можно отвлечься от его размеров, рассматривая движение лишь одной точки — центра тяжести. Понятие материальной точки, в этом случае принимает вполне реальный смысл.

Современное понятие силы, действующей на материальную точку, было дано еще Галилеем, сформулировавшим свой знаменитый закон инерции, из которого следует, что действующая на материальную точку сила изменяет ее состояние покоя или равномерного прямолинейного движения, т. е. сообщает точке ускорение. Определенные так силы Ньютон назвал ускоряющими. Направление силы, действующей на точку, определяется направлением вектора ускорения точки, которое последняя приобретает под действием силы.

Ньютон предложил измерять силу, действующую на материальную точку, тем ускорением, которое она сообщает материальной точке, считая величину силы пропорциональной величине ускорения. Такую силу можно представить вектором F, определяемым равенством

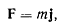
теоретическая механика

где j — ускорение точки; m — коэффициент пропорциональности, называемый м ассой материальной точки.

Первой системой мер, принятой для измерения силы, были меры веса. Это было вызвано тем, что первое представление о силе у человека возникло в связи с тем усилием, которое он должен был приложить, чтобы удержать груз рукой. Сравнение сил с весом может быть осуществлено при помощи динамометра, сравнивающего растяжение пружины силой с растяжением той же пружины подвешенным грузом. При таком измерении при помощи упругих деформаций две силы оказываются равными, если они производят одинаковые деформации или если их действия взаимно уничтожаются, когда эти силы заставляют действовать на одну и ту же точку по одной прямой, но в противоположные стороны.

Иногда в физике рассматривают силу как истинную реальность, существующую независимо от материальных объектов, которые являются ее источником или испытывают эффект ее действия, определяя силу независимо от движения, которое она способна произвести. Такая концепция противоречит определению силы, принятому в классической механике, и нами рассматриваться не будет. Мы будем каждый раз понимать силу как результат взаимодействия различных материальных объектов, не останавливаясь на выяснении физической природы взаимодействия, и будем измерять силу тем ускорением, которое она сообщает материальной точке.

Механика изучает физические законы природы. Законы эти устанавливаются в результате наблюдений, изучения природы. Обобщая многовековой опыт человечества, Галилей и Ньютон сформулировали основные законы механики, которые должны рассматриваться как аксиомы механики. Вся классическая механика строится на этих аксиомах, имеющих в основе экспериментальные факты. Для обоснования статики будем использовать следствия из основных законов Галилея—Ньютона, рассматривая эти следствия как самостоятельные аксиомы.

Лекции:

Аналитическая статика

При решении задач о равновесии в элементарной статике применяются исключительно геометрические методы, основанные на свойствах векторов.

Аналитическая статика дает другой метод исследования равновесия механических систем, в основе которого лежит понятие работы сил, действующих на исследуемую систему.

При наличии связей уравнения равновесия механической системы, получаемые геометрическим методом, кроме активных сил содержат еще и силы реакций, которые необходимо исключить из уравнений для определения возможных положений равновесия системы. Число подлежащих исключению реакций тем больше, чем больше связей наложено на исследуемую систему. Но поскольку силы реакции не создают движения системы, естественно искать такие условия равновесия, которые бы не содержали реакции связей. Эти условия могут быть получены при помощи принципа возможных перемещений.

Еще Аристотель использовал метод возможных перемещений при решении задачи о равновесии рычага. Галилеи применял его для исследования равновесия простейших машин. Однако окончательное завершение метод получил только в 1717 г. в работах И. Бернулли и Лагранжа. Швейцарский ученый И. Бер-нулли (1667—1748) первым показал общность принципа возможных перемещений и его преимущества при решении задач статики. Лагранж дал первое доказательство этого принципа. После Лагранжа появилось еще несколько других доказательств. Наиболее известные из них принадлежат Амперу, К. Нейману и Ж. Фурье (1768—1830).

Лекции:

Общие вопросы аналитической статики

Лекции:

Динамика

Динамика является главной частью механики. Она изучает движение различных механических систем и зависимости от причин, вызывающих это движение и влияющих на него. Причины эти в механике называются силами. Этим она и отличается от кинематики, которая при изучении движения материальных объектов не принимает во внимание причины, вызывающие это движение. В механике обычно не рассматривается происхождение сил, а изучается только их действие на движущиеся объекты. Изучение динамики начнем с задач о движении таких тел, размерами которых можно пренебрегать, а положение которых может быть определено как положение геометрической точки. Такие тела, или частицы материи, называют материальными точками. В теоретической механике все тела рассматриваются как совокупности взаимодействующих материальных точек. Одновременно с изменением положения каждое материальное тело, как бы мало оно ни было, может вращаться и деформироваться. Рассматривая движение материальной точки, будем изучать только изменение ее положения в пространстве, не интересуясь вращением и деформацией. Такое представление о материальной точке не лишено и реального смысла: подобной материальной точкой, с точки зрения механики, является центр тяжести твердого тела. В дальнейшем будет показано, что центр тяжести твердого тела движется как материальная точка, на которую действуют все силы, приложенные к этому телу.

Всякое движение материальной точки можно определить лишь по отношению к другим телам, а ее положение относительно других тел может быть задано тремя координатами, относящимися к определенному моменту времени. Обычно выбирают прямоугольные декартовы координаты, так как они проще связаны с длинами и расстояниями.

Всякое движение происходит во времени. Моменты времени, к которым относятся координаты и расстояния, а также промежутки времени, становятся определенными, когда выбрана определенная система отсчета. Измерение времени может быть в принципе произведено при помощи любого периодического процесса. В практике же принято астрономическое измерение времени, основанное на изучении законов движения планет и вращения земного шара. Фундаментальной единицей измерения времени являются звездные сутки — промежуток времени между двумя последовательными верхними кульминациями точки весеннего равноденствия. Время, протекшее от момента верхней кульминации точки весеннего равноденствия до любого другого момента, характеризуемого другим се положением, выраженное в долях звездных суток (звездных часах, минутах и секундах), называется звездным временем. Звездные сутки в качестве основной единицы времени неудобны, потому что начало суток при этой единице может приходиться последовательно на любое время дни и ночи. Но этой причине основной единицей времени выбрано среднегодовое значение солнечных суток — промежутка времени между двумя последовательными прохождениями Солнца через меридиан данного места на земной поверхности. Продолжительность солнечных с\ток зависит от годового движения Земли относительно Солнца, поэтому приходится брать среднегодовое значение солнечных суток. Практической единицей времени считается секунда среднего солнечного времени, равная 1/86400 средних солнечных суток, что составляет около 1/86164,09 звездных суток.

С 1 января 1963 г. в Советском Союзе введена международная система единиц СИ, в которой за единицу времени принята I секунда, равная 1/31556 925,9747 тропического года для 1900 г. января 0 в 12 часов эфемеридного времени, не зависящая от неравномерности вращения Земли.

Такой сопособ определения времени не является очень точным, поэтому в настоящее время для определения промежутков времени пользуются некоторыми естественными процессами, связанными с колебаниями атомов, период которых нечувствителен к внешним воздействиям. Но эти вопросы относятся уже к технике измерения времени и в курсе теоретической механики не изучаются.

Время, прошедшее между двумя событиями, называют промежутком времени, а границу между двумя промежутками называют моментом времени. В теоретической механике устанавливается независимо от событий или от системы, в которой наблюдаются события, соответствие между моментами времени и действительными числами. Определенное так время называют абсолютным идеальным временем.

Лекции:

Кстати теория из учебников по теоретической механике тут, может быть вам поможет она.

Возможно эти страницы вам будут полезны: