Оглавление:




Пределы применимости формулы Эйлера и построение полного графика критических напряжений
- Ограничения применимости уравнения Эйлера и построение полного графика критических напряжений. Результаты, полученные в предыдущем пункте, по-видимому, решают проблему испытания сжатого стержня на устойчивость. Но это далеко не так. Самое пристальное изучение фигур, полученных по формуле Эйлера, показывает, что она дает правильный результат только в известных
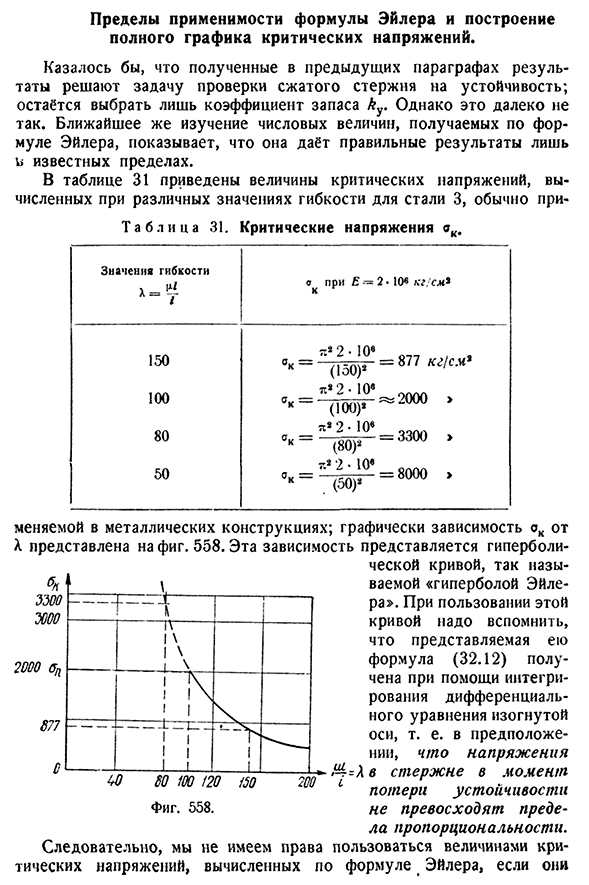
пределах. В таблице 31 приведены значения критических напряжений, рассчитанные с различными значениями гибкости для стали 3.- Т а б л и Ц А31. Критическое напряжение gk. Значение гибкости l-1 Е=2 * 106кг; см? Г. 2 2-10Э Сто пятьдесят По направлению к ° (150)2 =877 кг / см * L2 2 * 10E100^2 0 0 ″ К (100)’ Восемьдесят. _ _7X2 2 * 10Е С=3300 ″ (80)’ К2 2•10Е Фитти. Сэр=8000> К (50)2
На графике зависимость АК от А показана на рисунке. 558 эта зависимость представлена гиперболическими кривыми, так называемой Людмила Фирмаль
«гиперболой Эйлера». При использовании этой кривой необходимо помнить, что представленная ею формула (32.12) получается Интегралом дифференциального уравнения изогнутой оси. Поэтому мы не имеем права использовать значения критических напряжений, вычисленных в уравнении Эйлера, если они§ 203] предел применимости уравнения Эйлера 631 Выше этого предела для данного материала не получается. Другими словами, формула Эйлера применима только тогда, когда условия применимости формулы
Эйлера будут в другой форме, когда это неравенство (33.17) выражает гибкость X.: (33.18) Подставляя соответствующие значения модуля упругости и предела пропорциональности для заданного материала, вы получаете наименьшее значение гибкости, для чего можно использовать формулу Эйлера. Для стали 3 предел пропорциональности будет равен ZP=2000 кг) см\поэтому, как видно
- из таблицы 31 и формулы (33.18), необходимо говорить о стержнях из этого материала. Сто., То есть больше 100. Для стали 5 AP3000KzjcM * формула Эйлера применима в гибкости X85;для чугуна-X80,для сосны-X^N O и др…。 Если это так. 558op = нарисуйте вертикальную линию, равную 2000 км) см\она разрежет гиперболу Эйлера на две части; вы можете увидеть график, связанный с относительно тонким и длинным стержнем. Теоретическое решение, полученное Эйлером, было применено на практике к стержню очень ограниченной категории, то есть тонкому и длинному, очень гибкому. С другой стороны, конструктивно очень часто встречаются менее гибкие
стержни. Попытка рассчитать критическое напряжение и проверить устойчивость при малых изгибах с использованием формулы Эйлера привела в некоторых случаях к очень серьезной катастрофе, и в результате экспериментов по сжатию стержней было установлено, что фактическая критическая сила при критическом напряжении, превышающем предел пропорциональности, была значительно ниже, чем та, которая была определена формулой Эйлера. Поэтому необходимо найти способ расчета критического напряжения, которое может быть достигнуто, если оно превышает пределы пропорциональности материала, например,
от 0 до 100 прутка мягкой стали. Следует отметить, что в настоящее время наиболее важным источником установления критического Людмила Фирмаль
напряжения за пределами пропорциональности, то есть малой и средней гибкости, является результат эксперимента. Предпринимаются попытки проверить устойчивость сжатого стержня[глава XXXIII И теоретическое решение этой проблемы они указывают путь к дальнейшим исследованиям, а не дают практических оснований для расчетов. Прежде всего, необходимо выделить стержень с низкой гибкостью порядка 30-40 градусов. Например, для стержня круглого поперечного сечения 20 соответствует отношению длины к диаметру 5. Для такого стержня можно говорить о явлении потери устойчивости прямой формы всего стержня, в том смысле, что это имеет место в случае с тонкими и длинными стержнями. Эти короткие стержни выходят из строя
в основном из-за того, что напряжение сжатия достигает предела текучести ZT (пластичный материал) или предела прочности s (хрупкий материал). Так, для коротких стержней критическое напряжение равно или несколько ниже, соответственно, или от (сталь), или АВ (чугун, дерево), вплоть до гибкости порядка 30-40. Поэтому в случае сжатого стержня, короткого стержня, который теряет несущую способность главным образом из-за разрушения материала сжатием, и потери несущей способности, стабильности прямолинейной формы стержня количественные изменения соотношения длины стержня и поперечного размера изменяют весь характер явления разрушения. Общим является резкость наступления критического состояния в смысле внезапного резкого увеличения
деформации. В сжатых стержнях большой гибкости, где применима формула Эйлера, резкое увеличение деформации обычно наблюдается после того, как сила P достигает критического значения. До этого момента прогиб имеет тенденцию увеличиваться с увеличением нагрузки, но остается незначительным. Теоретически стержень должен идти прямо до критической силы, однако на практике возникает ряд неизбежных обстоятельств-начальная кривизна стержня, некоторый эксцентриситет приложения нагрузки, локальное перенапряжение, неоднородность материала-малый прогиб и неравномерность. Аналогичное свойство имеет зависимость укорочения от сжимающего напряжения коротких стержней. Теперь
нам остается рассмотреть поведение сжатых стержней при среднем значении гибкости, например, для стальных стержней при 40-100 гибкостях; аналогично§ 203 гибкостей] предел применимости уравнения Эйлера 633. По характеру разрушения эти стержни приближаются к категории тонких и длинных стержней. В экспериментах для них можно отметить наличие критической силы, которая четко выражена в»Эйлеровом» смысле. Однако, по сравнению с короткими стержнями для этих» средних » гибких стержней, потеря прямой формы и уменьшение критического напряжения вытягивают потерю несущей способности коротких
стержней, здесь мы объединяем эффект эффекта длины, уменьшающего величину критического напряжения, и эффект значительного увеличения деформации материала при напряжении за пределом пропорциональности. Экспериментальное определение критической силы для сжатого стержня неоднократно проводилось в стране и за рубежом. Особенно велик ОП ы ТН ы материалов, проф. проф, который составил таблицу напряжений («разрывных»), важных по гибкости для ряда материалов. Давление для собирать и стабилности). На основании полученного экспериментального материала, при критическом напряжении меньше предела
пропорциональности, можно предположить, что все эксперименты подтверждают эйлерово выражение любого материала. Для стержня со средней и малой гибкостью были предложены различные эмпирические формулы, критическое напряжение в такой гибкости может изменяться по закону, близкому к линейному. *): *)Я с и Н С К и й, собрание сочинений, Т. Я. Петербург, 1902. OK=a-B(33.19), где a и b-коэффициенты, зависящие от материала, а X=~ — гибкость стержня. Для чугуна Ясинский получил: а= = 3387 кг) см\6=1 4,8 3 кг).Для стали можно взять коэффициенты гибкости
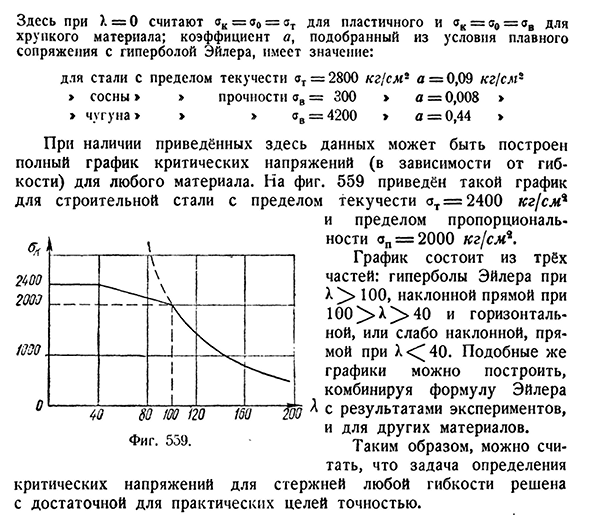
a и b от cm3X=40 до X=100:a=3360K\g) cm B=^1. кг) для других материалов г1см данные по коэффициентам а и 6 приведены в справочнике (например, смотрите справку изд. Динник, Москва, 1949). Иногда эмпирическая формула удобна, давая изменение критического напряжения в соответствии с параболическим законом квадрата для неупругой области.(33.20)634 проверка сжатого стержня на устойчивость [глава XXXIII Здесь для X=O коэффициент a, выбранный из условий гладкой связи ak=a0=zt для пластика, для хрупких материалов AK=g0=AB, гиперболического Эйлера и т. д., равен at=2800kg[cm? a-кг / см — > сосна> «прочность AB=300>a=0.008> „чугун“ > » AB=4200>a=0.44″ » С данными, представленными здесь, полный график критического давления (в зависимости от гибкости) може
т быть запланирован для любого материала. Как использовать 559 такой график приведен для конструкционной стали с пределом текучести пропорционального предела АТ=2 4 0 0 кг[сми АП = 2000 кг[см*. Граф состоит из гиперболы Эйлера X>100, линии наклона 100X40 и горизонтальной или слабой линии наклона X<^40. Аналогичный график можно построить, объединив формулу Эйлера а с экспериментальными результатами, а также с другими материалами. Поэтому можно предположить, что задача определения критического напряжения для любого гибкого стержня решается с достаточной точностью для практических целей.
Смотрите также:
| Формула Эйлера для критической силы. | Проверка сжатых стержней на устойчивость. |
| Влияние способа закрепления концов стержня | Выбор типа сечения и материала |

