Оглавление:
На практике довольно часто встречается ситуация, когда многократно наблюдается, как сказал бы не знакомый с теорией вероятностей человек, «одна и та же» случайная величина, а конечный результат представляет собой сумму наблюденных в каждом испытании значений этих величин. Наряду с уже упоминавшимися азартными играми сюда можно отнести: повторные замеры одного и того же параметра с последующим осреднением результатов с целью повышения точности измерений; многократное воздействие однородных причин на некоторый протекающий во времени физический процесс и т. д. Пройденный нами путь по теории вероятностей и приобретенный при этом опыт применения основных ее понятий позволяют подойти к описанию всех этих явлений с единых вероятностных позиций на основе следующей схемы: имеется последовательность независимых одинаково распределенных случайных величин и из нее образуется среднее арифметическое первых п членов. Спрашивается, как будет вести себя это среднее арифметическое, если п велико? Оказывается, при большом п оно теряет свойство случайности и приближается к математическому ожиданию каждого слагаемого (отсюда второе название математического ожидания — среднее значение). Этот факт носит название закона больших чисел. Собственно говоря, с частным случаем закона больших чисел мы уже встречались, когда рассматривали схему Бернулли (теорема Бернулли). Следуя исторической традиции, доказательство закона больших чисел мы сначала проведем, опираясь на неравенство Чебышева, которое является родоначальником многих других неравенств, широко применяемых в современной теории вероятностей.
Дальнейшее уточнение закона больших чисел происходило в двух направлениях. Первое связано с динамикой поведения средних арифметических. К основным результатам этого направления следует отнести усиленный закон больших чисел и закон повторного логарифма, полученные А. Н. Колмогоровым. Исходным пунктом второго направления, называемого иногда центральной предельной проблемой, являются теоремы Муавра-Лапласа. Решение центральной предельной проблемы позволило описать класс всех распределений, которые могут выступать в качестве предельных для функций распределения сумм независимых случайных величин в том случае, когда вкладом каждого слагаемого можно пренебречь, найти необходимые и достаточные условия сходимости к каждому распределению этого класса, оценить скорость сходимости. Простейшим примером результатов такого типа является центральная предельная теорема для одинаково распределенных слагаемых, имеющих дисперсию, которую мы докажем в параграфе 4. Основным математическим аппаратом при решении центральной предельной проблемы служит преобразование Фурье, носящее в теории вероятностей название характеристической функции, хотя в последнее время все чаще применяются другие методы.
Неравенство Чебышева. Закон больших чисел
Рассмотрим случайную величину 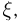 имеющую дисперсию
имеющую дисперсию 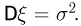 Мы уже говорили, что дисперсия является показателем разброса
Мы уже говорили, что дисперсия является показателем разброса  вокруг математического ожидания
вокруг математического ожидания 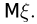 Однако с точки зрения исследователя разброс естественнее характеризовать вероятностью
Однако с точки зрения исследователя разброс естественнее характеризовать вероятностью 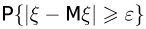 отклонения случайной величины
отклонения случайной величины 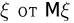 на величину, большую некоторого заданного
на величину, большую некоторого заданного 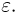 Следующее неравенство позволяет оценить эту вероятность через дисперсию
Следующее неравенство позволяет оценить эту вероятность через дисперсию 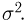
Неравенство Чебышева. Для каждой случайной величины 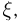 имеющей дисперсию
имеющей дисперсию 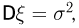 при любом
при любом 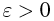 справедливо неравенство
справедливо неравенство
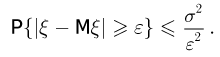
Доказательство проведем для непрерывной случайной величины  с плотностью распределения р(х). По определению,
с плотностью распределения р(х). По определению,
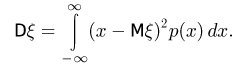
Поскольку подынтегральное выражение неотрицательно, то при уменьшении области интегрирования интеграл может только уменьшиться, поэтому
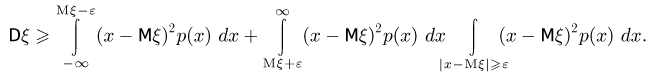
Учитывая теперь, что 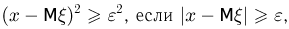 получаем
получаем
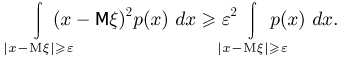
Остается заметить, что последний интеграл представляет собой вероятность события 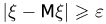 и, значит,
и, значит,
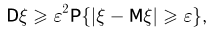
откуда и вытекает неравенство Чебышева.
Аналогично неравенство Чебышева доказывается и для дискретного случая, при этом нужно только заменить интеграл на сумму.
Ясно, что применять неравенство Чебышева имеет смысл только тогда, когда 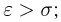 в противном случае оно дает тривиальную оценку.
в противном случае оно дает тривиальную оценку.
Пример:
Пусть случайная величина  имеет плотность распределения
имеет плотность распределения 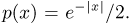 Тогда
Тогда 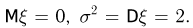 Воспользовавшись неравенством Чебышева, оценим
Воспользовавшись неравенством Чебышева, оценим 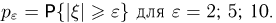 В результате получим
В результате получим
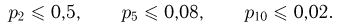
С другой стороны, поскольку 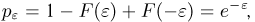 имеем
имеем
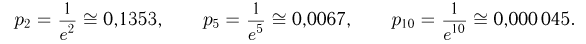
Таким образом, в этом примере неравенство Чебышева дает очень грубую оценку вероятности 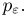
Пример:
Пусть случайная величина 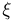 принимает только два значения 1 и — 1 с одинаковыми вероятностями 1/2. Тогда
принимает только два значения 1 и — 1 с одинаковыми вероятностями 1/2. Тогда 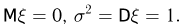 Применяя неравенство Чебышева, получаем
Применяя неравенство Чебышева, получаем 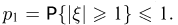 С другой стороны, поскольку оба возможных значения
С другой стороны, поскольку оба возможных значения 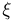 равны по модулю единице, то
равны по модулю единице, то 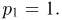
Этот пример показывает, что если не делать никаких дополнительных предположений относительно случайной величины 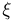 то неравенство Чебышева дает неулучшаемую оценку
то неравенство Чебышева дает неулучшаемую оценку 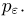
Рассмотрим теперь последовательность  независимых одинаково распределенных случайных величин (так как случайные величины
независимых одинаково распределенных случайных величин (так как случайные величины 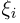 одинаково распределены, то все их числовые характеристики, в частности математические ожидания и дисперсии, равны между собой). Скажем, что эта последовательность удовлетворяет (слабому) закону больших чисел, если для некоторого а и любого
одинаково распределены, то все их числовые характеристики, в частности математические ожидания и дисперсии, равны между собой). Скажем, что эта последовательность удовлетворяет (слабому) закону больших чисел, если для некоторого а и любого 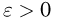
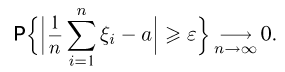
Иными словами, выполнение закона больших чисел отражает предельную устойчивость средних арифметических случайных величин: при большом числе испытаний они практически перестают быть случайными и с большой степенью достоверности могут быть предсказаны.
Иногда вместо выражения «последовательность  удовлетворяет закону больших чисел» говорят «среднее арифметическое случайных величин
удовлетворяет закону больших чисел» говорят «среднее арифметическое случайных величин  сходится по вероятности к некоторой предельной постоянной а».
сходится по вероятности к некоторой предельной постоянной а».
Теорема (закон больших чисел)
Теорема:
Закон больших чисел. Если последовательность  независимых одинаково распределенных случайных величин такова, что существуют
независимых одинаково распределенных случайных величин такова, что существуют 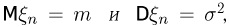 то для любого
то для любого 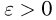
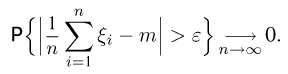
Доказательство является элементарным следствием неравенства Чебышева. Действительно, по свойствам математического ожидания и дисперсии
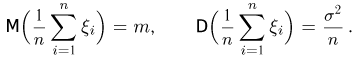
Воспользовавшись теперь неравенством Чебышева, получаем, что для любого 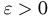
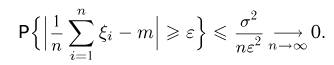
Таким образом, мы показали, что для последовательности  выполняется закон больших чисел, причем постоянная а совпадает с математическим ожиданием
выполняется закон больших чисел, причем постоянная а совпадает с математическим ожиданием 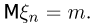
Пример:
Пусть 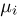 — число успехов в i-м испытании Бернулли (см. пример 2 в гл. 6). Тогда
— число успехов в i-м испытании Бернулли (см. пример 2 в гл. 6). Тогда 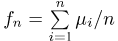 представляет собой частоту успехов в п испытаниях. Как мы знаем,
представляет собой частоту успехов в п испытаниях. Как мы знаем, 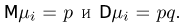 Таким образом, в силу доказанной теоремы
Таким образом, в силу доказанной теоремы
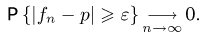
Но последнее соотношение есть не что иное, как теорема Бернулли (см. параграф 5 гл. 4).
Замечание:
Вообще говоря, существование дисперсии является достаточным, но не необходимым условием для выполнения закона больших чисел. В дальнейшем (пример 15) будет показано, что достаточным условием является просто существование математического ожидания, которое в этом случае выступает в качестве предельной постоянной а. Более того, существуют последовательности независимых одинаково распределенных случайных величин, даже не имеющих математического ожидания, но тем не менее удовлетворяющих закону больших чисел.
Усиленный закон больших чисел. Закон повторного логарифма
Пусть по-прежнему 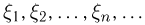 — последовательность независимых одинаково распределенных случайных величин, к которой применим закон больших чисел, т.е. при больших п среднее арифметическое
— последовательность независимых одинаково распределенных случайных величин, к которой применим закон больших чисел, т.е. при больших п среднее арифметическое 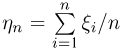 «почти совпадает» с некоторой постоянной а. Однако если мы будем последовательно наблюдать случайные величины
«почти совпадает» с некоторой постоянной а. Однако если мы будем последовательно наблюдать случайные величины 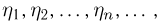 то закон больших чисел еще не гарантирует, что
то закон больших чисел еще не гарантирует, что 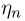 будет стремиться к а для любого элементарного исхода
будет стремиться к а для любого элементарного исхода 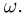
Пример:
Рассмотрим схему Бернулли с равными вероятностями успеха и неудачи 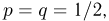 в которой производится бесконечное число испытаний. Тогда последовательность
в которой производится бесконечное число испытаний. Тогда последовательность 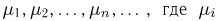 число успехов в i-м испытании, будет представлять собой простейший вариант последовательности независимых одинаково распределенных случайных величин, для которой в соответствии с теоремой Бернулли выполнен закон больших чисел и при этом
число успехов в i-м испытании, будет представлять собой простейший вариант последовательности независимых одинаково распределенных случайных величин, для которой в соответствии с теоремой Бернулли выполнен закон больших чисел и при этом 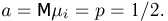
Пространство элементарных исходов 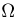 состоит из всевозможных (бесконечных) последовательностей УНН…УН… В отличие от случая конечного числа испытаний
состоит из всевозможных (бесконечных) последовательностей УНН…УН… В отличие от случая конечного числа испытаний 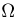 уже не будет дискретным (более того,
уже не будет дискретным (более того, 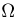 «почти» эквивалентно отрезку [0,1] с равномерной вероятностью на нем; для доказательства этого достаточно отождествить последовательность
«почти» эквивалентно отрезку [0,1] с равномерной вероятностью на нем; для доказательства этого достаточно отождествить последовательность  с двоичным представлением некоторого числа, заключенного между нулем и единицей), и каждый элементарный исход
с двоичным представлением некоторого числа, заключенного между нулем и единицей), и каждый элементарный исход 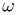 имеет вероятность
имеет вероятность 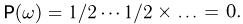 Возьмем элементарный исход
Возьмем элементарный исход 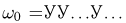 Ясно, что для него
Ясно, что для него 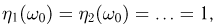 т.е. средние арифметические равны единице и не могут стремиться к
т.е. средние арифметические равны единице и не могут стремиться к 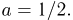 Читатель без труда может привести примеры и других элементарных исходов, для которых последовательность
Читатель без труда может привести примеры и других элементарных исходов, для которых последовательность 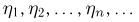 либо будет сходиться к отличному от 1/2 числу, либо вообще не будет сходиться.
либо будет сходиться к отличному от 1/2 числу, либо вообще не будет сходиться.
Из приведенного выше примера видно, что могут существовать элементарные исходы, для которых 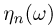 не сходится к а. Выделим эти элементарные исходы в отдельное событие ,4. Хотелось бы, чтобы при выполнении закона больших чисел вероятность события А равнялась нулю; в этом случае говорят, что для последовательности
не сходится к а. Выделим эти элементарные исходы в отдельное событие ,4. Хотелось бы, чтобы при выполнении закона больших чисел вероятность события А равнялась нулю; в этом случае говорят, что для последовательности 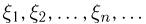 выполнен усиленный закон больших чисел. Но это не всегда так. Если заранее не предполагать существование математического ожидания
выполнен усиленный закон больших чисел. Но это не всегда так. Если заранее не предполагать существование математического ожидания 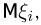 то можно привести примеры последовательностей независимых одинаково распределенных случайных величин, для которых выполнен закон больших чисел, но не выполнен усиленный закон больших чисел (более подробно об этом см. ниже, пример 15). Условие выполнения усиленного закона больших чисел содержится в следующей теореме, доказанной А. Н. Колмогоровым.
то можно привести примеры последовательностей независимых одинаково распределенных случайных величин, для которых выполнен закон больших чисел, но не выполнен усиленный закон больших чисел (более подробно об этом см. ниже, пример 15). Условие выполнения усиленного закона больших чисел содержится в следующей теореме, доказанной А. Н. Колмогоровым.
Теорема (усиленный закон больших чисел)
Теорема:
Усиленный закон больших чисел. Существование математического ожидания является необходимым и достаточным условием выполнения усиленного закона больших чисел для последовательности независимых одинаково распределенных случайных величин 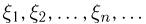 Постоянная а в этом случае совпадает с математическим ожиданием
Постоянная а в этом случае совпадает с математическим ожиданием 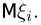
Доказательство теоремы Колмогорова мы здесь не приводим.
Отметим, что выполнение усиленного закона больших чисел естественно влечет за собой выполнение закона больших чисел.
Если теперь перейти от средних арифметических к накопленным суммам 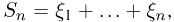 то усиленный закон больших чисел гласит, что последовательность
то усиленный закон больших чисел гласит, что последовательность 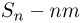 для почти всех элементарных исходов при любом
для почти всех элементарных исходов при любом 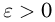 может находиться выше уровня
может находиться выше уровня 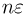 или ниже уровня —
или ниже уровня —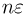 не более конечного числа раз. Зададим теперь вопрос: нельзя ли указать более точные границы изменения последовательности
не более конечного числа раз. Зададим теперь вопрос: нельзя ли указать более точные границы изменения последовательности 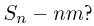 Естественно, если мы хотим больше получить, то мы должны также больше потребовать от случайных величин
Естественно, если мы хотим больше получить, то мы должны также больше потребовать от случайных величин 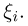 А именно, будем предполагать, что
А именно, будем предполагать, что 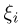 имеют математическое ожидание
имеют математическое ожидание 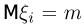 и дисперсию
и дисперсию 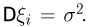 Для простоты изложения предположим, что
Для простоты изложения предположим, что 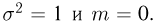 Более того, будем считать, что абсолютные значения случайных величин
Более того, будем считать, что абсолютные значения случайных величин 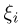 ограничены, т. е. существует такое число X, что
ограничены, т. е. существует такое число X, что 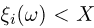 для всех элементарных исходов
для всех элементарных исходов 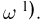 Из последнего предположения, в частности следует, что случайные величины
Из последнего предположения, в частности следует, что случайные величины 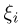 имеют не только математическое ожидание и дисперсию, но и моменты всех порядков.
имеют не только математическое ожидание и дисперсию, но и моменты всех порядков.
Для произвольного 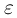 обозначим через
обозначим через 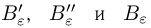 события, состоящие соответственно из тех элементарных исходов
события, состоящие соответственно из тех элементарных исходов 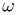 для которых
для которых  бесконечное число раз,
бесконечное число раз, 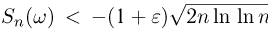 бесконечное число раз и
бесконечное число раз и 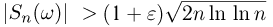 бесконечное число раз.
бесконечное число раз.
Теорема (закон повторного логарифма)
Теорема:
Закон повторного логарифма. 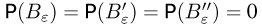 для любых
для любых 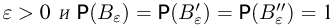 для любых
для любых 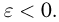
Доказательство теоремы опирается на очень тонкие (так называемые показательные) вероятностные неравенства и также здесь не приводятся.
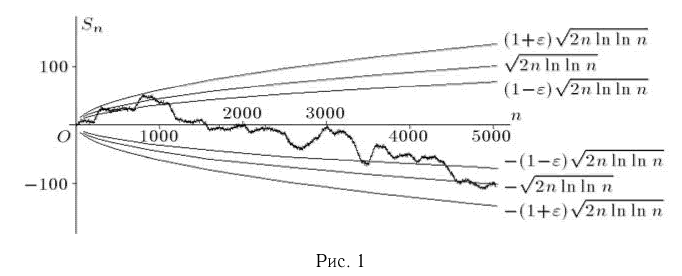
Смысл закона повторного логарифма заключается в следующем. Для любого сколь угодно малого 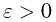 накопленные суммы
накопленные суммы 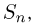 начиная с некоторого п, будут лежать в пределах от
начиная с некоторого п, будут лежать в пределах от 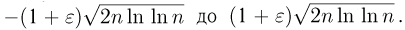 В то же время суммы
В то же время суммы 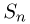 будут бесконечное число раз выходить за границы области, находящейся между кривыми
будут бесконечное число раз выходить за границы области, находящейся между кривыми 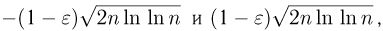 причем как вверх, так и вниз (рис. 1).
причем как вверх, так и вниз (рис. 1).
Для читателя, знакомого с понятием верхнего и нижнего пределов  последовательности, можно предложить следующую формулировку закона повторного логарифма: для почти всех элементарных исходов
последовательности, можно предложить следующую формулировку закона повторного логарифма: для почти всех элементарных исходов 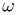
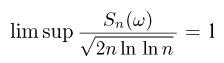
и
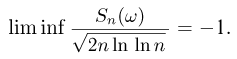
Отметим, что само название «закон повторного логарифма» происходит от выражения 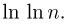
Характеристическая функция
Для дальнейших исследований нам понадобится понятие характеристической функции. Характеристической функцией 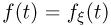 случайной величины
случайной величины 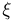 называется математическое ожидание случайной величины
называется математическое ожидание случайной величины 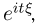 где
где 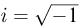 — мнимая единица, a t — произвольное (действительное) число. Здесь мы имеем дело с комплексной случайной величиной, которая определяется так же, как и действительная, с той лишь разницей, что каждому элементарному исходу ставится в соответствие комплексное число, а не действительное. Используя общее правило вычисления математического ожидания и формулу Эйлера, получаем
— мнимая единица, a t — произвольное (действительное) число. Здесь мы имеем дело с комплексной случайной величиной, которая определяется так же, как и действительная, с той лишь разницей, что каждому элементарному исходу ставится в соответствие комплексное число, а не действительное. Используя общее правило вычисления математического ожидания и формулу Эйлера, получаем
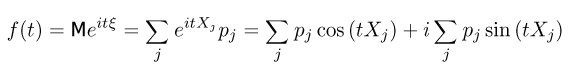
для дискретной величины 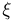 и
и
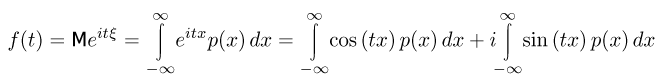
для непрерывной. Поскольку 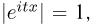 то характеристическая функция существует при всех (действительных) t для каждой случайной величины. Отметим, что характеристическая функция определяется не собственно случайной величиной, а ее функцией распределения, т. е. по существу характеризует именно распределение случайной величины. Читатель, знакомый с преобразованием Фурье, сразу же заметит, что характеристическая функция непрерывной случайной величины отличается от преобразования Фурье плотности распределения этой случайной величины только лишь отсутствием множителя
то характеристическая функция существует при всех (действительных) t для каждой случайной величины. Отметим, что характеристическая функция определяется не собственно случайной величиной, а ее функцией распределения, т. е. по существу характеризует именно распределение случайной величины. Читатель, знакомый с преобразованием Фурье, сразу же заметит, что характеристическая функция непрерывной случайной величины отличается от преобразования Фурье плотности распределения этой случайной величины только лишь отсутствием множителя 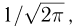 что, как будет видно из дальнейшего, представляет определенное удобство при действиях над случайными величинами.
что, как будет видно из дальнейшего, представляет определенное удобство при действиях над случайными величинами.
Пример:
Найдем характеристическую функцию случайной величины 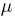 распределенной по биномиальному закону. Поскольку
распределенной по биномиальному закону. Поскольку 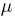 — дискретная случайная величина, принимающая значения 0,1,…,п, то
— дискретная случайная величина, принимающая значения 0,1,…,п, то
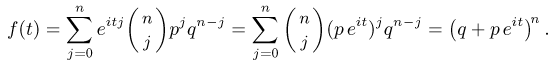
Пример:
Характеристическая функция случайной величины 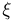 распределенной по экспоненциальному закону, имеет вид
распределенной по экспоненциальному закону, имеет вид
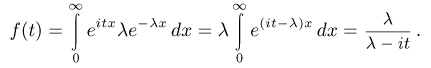
Пример:
Пусть случайная величина 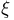 распределена по стандартному нормальному закону. Тогда
распределена по стандартному нормальному закону. Тогда
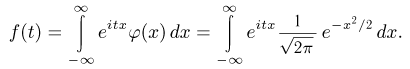
Делая замену 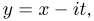 получаем
получаем
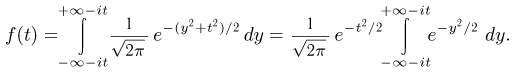
Из теории функций комплексного переменного известно, что
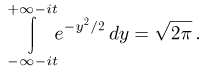
Поэтому окончательно получаем
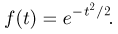
Выведем некоторые почти очевидные свойства характеристических функций.
 — непрерывная функция.
— непрерывная функция.
В самом деле (рассмотрим, например, дискретный случай)
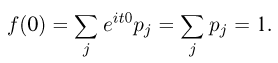
Непрерывность 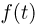 следует из непрерывности функции
следует из непрерывности функции  и абсолютной сходимости ряда
и абсолютной сходимости ряда 
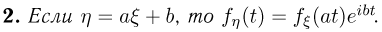
Действительно, из определения характеристической функции и свойств математического ожидания вытекает, что
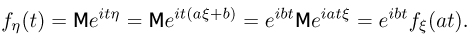
Пусть 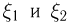 — независимые случайные величины и
— независимые случайные величины и 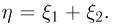 Тогда
Тогда
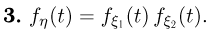
В самом деле, поскольку 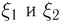 независимы, то независимы случайные величины
независимы, то независимы случайные величины 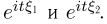 Отсюда следует, что
Отсюда следует, что
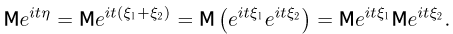
Именно свойство 3 является тем основным свойством, благодаря которому характеристические функции нашли такое широкое применение в теории вероятностей. При суммировании независимых случайных величин их плотности распределения преобразуются по формуле свертки.
Но формула свертки весьма неудобна для исследования, гораздо проще заменить ее простым перемножением характеристических функций.
Если случайная величина 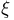 имеет момент n-го порядка
имеет момент n-го порядка 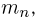 то характеристическая функция
то характеристическая функция  дифференцируема п раз, причем для
дифференцируема п раз, причем для 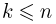
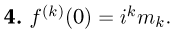
В самом деле, формальное дифференцирование характеристической функции k раз 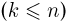 дает (например, в непрерывном случае)
дает (например, в непрерывном случае)
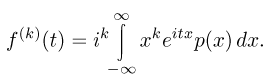
Законность дифференцирования определяется тем фактом, что
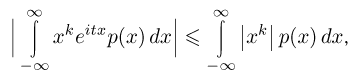
и существованием момента n-го порядка. Заметим, что при четном п справедливо и обратное: если характеристическая функция имеет производную 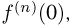 то существуют моменты
то существуют моменты 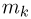 всех порядков k до п-го включительно и
всех порядков k до п-го включительно и 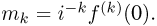
Пример:
Как мы знаем, если случайная величина 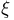 распределена по стандартному нормальному закону, то случайная величина
распределена по стандартному нормальному закону, то случайная величина 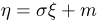 распределена по нормальному закону с параметрами
распределена по нормальному закону с параметрами 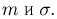 Тогда характеристические функции
Тогда характеристические функции 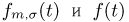 случайных величин
случайных величин 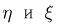 связаны по свойству 2 соотношением
связаны по свойству 2 соотношением
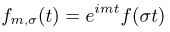
или, если учесть результат примера 7,
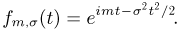
Пример:
Вычислим момент n-го порядка случайной величины 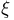 распределенной по экспоненциальному закону. Воспользовавшись свойством 4 и результатом примера 6, получаем
распределенной по экспоненциальному закону. Воспользовавшись свойством 4 и результатом примера 6, получаем
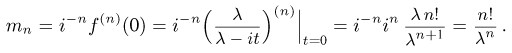
Пример:
Найдем еще раз характеристическую функцию числа успехов 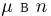 испытаниях, однако в отличие от примера 5 воспользуемся тем, что
испытаниях, однако в отличие от примера 5 воспользуемся тем, что 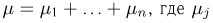 — число успехов в j-м испытании. Тогда
— число успехов в j-м испытании. Тогда
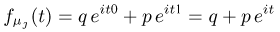
и, значит, по свойству 3
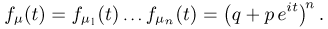
Важнейшей особенностью характеристической функции 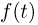 является тот факт, что она однозначно определяет функцию распределения F(x). А именно, справедлива следующая формула.
является тот факт, что она однозначно определяет функцию распределения F(x). А именно, справедлива следующая формула.
Формула обращения
Формула обращения. Для любых точек непрерывности 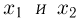 функции распределения F(x) приращение
функции распределения F(x) приращение
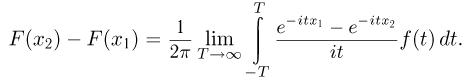
Отметим, что формула обращения справедлива и в точках разрыва F(x), если считать, что в этих точках 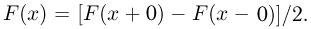
Не давая строгого математического доказательства, покажем, что по своей сути формула обращения представляет собой разновидность обратного преобразования Фурье. Действительно, формально применяя обратное преобразование Фурье к характеристической функции 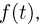 получаем следующее выражение для плотности распределения р(х):
получаем следующее выражение для плотности распределения р(х):
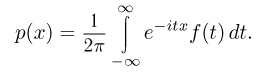
Далее, вспоминая соотношение между плотностью распределения р(х) и функцией распределения F(x), имеем
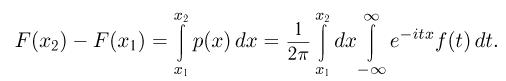
Еще раз производя формальную операцию — перестановку интегралов, получаем
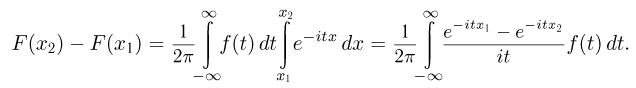
Хотя каждая из произведенных формальных операций, вообще говоря, математически не обоснована (в частности, дискретные случайные величины вообще не имеют плотности распределения), как это часто бывает, конечный результат верен, если только понимать последний интеграл в том смысле, как написано в формуле обращения (в смысле главного значения).
Определение характеристической функции вместе с формулой обращения устанавливают взаимно однозначное соответствие между функцией распределения и характеристической функцией.
Пример:
Пусть 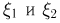 — независимые случайные величины, распределенные по нормальному закону с параметрами
— независимые случайные величины, распределенные по нормальному закону с параметрами 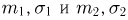 соответственно. Рассмотрим случайную величину
соответственно. Рассмотрим случайную величину 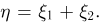 Тогда, как было показано в примере 8,
Тогда, как было показано в примере 8, 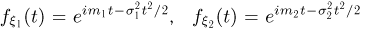 свойству 3 характеристических функций получаем, что
свойству 3 характеристических функций получаем, что 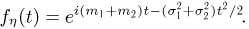 Но характеристическую функцию
Но характеристическую функцию 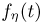 имеет случайная величина, распределенная по нормальному закону с параметрами
имеет случайная величина, распределенная по нормальному закону с параметрами 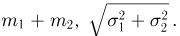 Поэтому в силу взаимно однозначного соответствия между функцией распределения и характеристической функцией случайная величина
Поэтому в силу взаимно однозначного соответствия между функцией распределения и характеристической функцией случайная величина 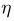 также распределена нормально (с параметрами
также распределена нормально (с параметрами 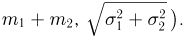
Пример:
Рассмотрим независимые случайные величины 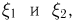 распределенные по закону Пуассона с параметрами
распределенные по закону Пуассона с параметрами 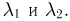 Их характеристические функции задаются формулами
Их характеристические функции задаются формулами
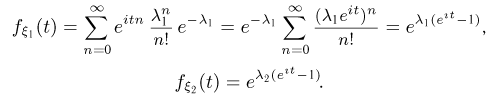
Пусть 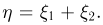 Тогда
Тогда 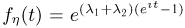 и опять-таки в силу взаимно однозначного соответствия между функцией распределения и характеристической функцией случайная величина
и опять-таки в силу взаимно однозначного соответствия между функцией распределения и характеристической функцией случайная величина 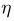 распределена по закону Пуассона с параметром
распределена по закону Пуассона с параметром 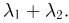
Основную роль при решении центральной предельной проблемы играет теорема о связи сходимости последовательности функций распределения со сходимостью последовательности соответствующих характеристических функций, или теорема непрерывности. Однако прежде чем перейти к формулировке этой теоремы, скажем несколько слов вообще о сходимости функций распределения. Будем говорить, что последовательность функций распределения 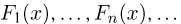 сходится к предельной функции распределения F(x), если
сходится к предельной функции распределения F(x), если  для любых х, являющихся точками непрерывности F(x). Такая сходимость называется слабой сходимостью функций распределения (обозначается
для любых х, являющихся точками непрерывности F(x). Такая сходимость называется слабой сходимостью функций распределения (обозначается 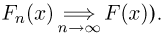 Слабая сходимость является наиболее естественной для функций распределения, и в дальнейшем мы будем рассматривать только ее.
Слабая сходимость является наиболее естественной для функций распределения, и в дальнейшем мы будем рассматривать только ее.
К определению слабой сходимости можно сделать несколько замечаний.
Во-первых, из слабой сходимости последовательности функций распределения еще нельзя сделать вывод о какой-либо сходимости последовательности самих случайных величин, так как даже одинаково распределенные случайные величины могут быть заданы на совершенно разных вероятностных пространствах.
Во-вторых, требование сходимости в любой точке непрерывности F(x) нельзя заменить более сильным требованием сходимости во всех точках х. Это подтверждает следующий пример.
Пример:
Пусть на одном и том же вероятностном пространстве 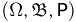 задана последовательность случайных величин
задана последовательность случайных величин 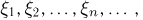 причем каждая случайная величина
причем каждая случайная величина 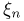 принимает всего одно значение -1 /п. Тогда последовательность
принимает всего одно значение -1 /п. Тогда последовательность 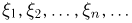 будет сходиться к случайной величине
будет сходиться к случайной величине 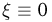 для любого элементарного исхода
для любого элементарного исхода 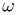 (причем даже равномерно). Тем не менее, F$n(0) = 1 при всех п, но
(причем даже равномерно). Тем не менее, F$n(0) = 1 при всех п, но 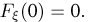
Приведенный пример показывает, что 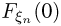 не стремится к
не стремится к 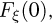 хотя естественно было бы ожидать сходимости
хотя естественно было бы ожидать сходимости 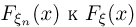 в любой точке х, поскольку
в любой точке х, поскольку 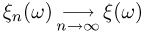 при всех элементарных исходах
при всех элементарных исходах 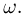
Разгадка этого парадокса заключается в том, что 0 является точкой разрыва 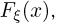 а при определении слабой сходимости функций распределения сходимости в таких точках мы не требовали.
а при определении слабой сходимости функций распределения сходимости в таких точках мы не требовали.
Наконец, если последовательность функций распределения 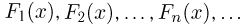 сходится к некоторой функции F(x) в каждой точке непрерывности последней, то это не гарантирует слабой сходимости, поскольку F(x) может вообще не быть функцией распределения.
сходится к некоторой функции F(x) в каждой точке непрерывности последней, то это не гарантирует слабой сходимости, поскольку F(x) может вообще не быть функцией распределения.
Пример 14. Пусть 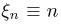 для всех
для всех 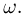 Тогда
Тогда 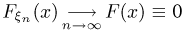 при каждом х. Но F(x) не является функцией распределения, так как
при каждом х. Но F(x) не является функцией распределения, так как 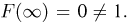
Значит, при определении слабой сходимости обязательно нужно требовать, чтобы предельная функция являлась функцией распределения.
Теперь мы можем привести (без доказательства) формулировку теоремы непрерывности.
Теорема непрерывности
Теорема непрерывности:
Для того чтобы последовательность функций распределения 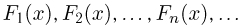 слабо сходилась к функции распределения F(x), необходимо и достаточно, чтобы последовательность характеристических функций
слабо сходилась к функции распределения F(x), необходимо и достаточно, чтобы последовательность характеристических функций 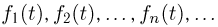 сходилась к характеристической функции
сходилась к характеристической функции 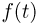 равномерно на любом отрезке
равномерно на любом отрезке 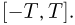
Теорема непрерывности является тем краеугольным камнем, который позволяет свести задачу изучения предельного поведения распределений сумм независимых случайных величин к задаче изучения предельного поведения характеристических функций этих сумм. Отметим, что в разных учебниках приведены различные эквивалентные формулировки теоремы непрерывности; данная здесь формулировка наиболее естественна для наших дальнейших рассуждений.
Пример:
Пусть 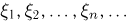 — последовательность независимых одинаково распределенных случайных величин, имеющих характеристические функции
— последовательность независимых одинаково распределенных случайных величин, имеющих характеристические функции 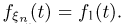 Рассмотрим последовательность средних арифметических
Рассмотрим последовательность средних арифметических 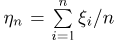 и найдем в терминах характеристических функций необходимое и достаточное условие для выполнения (слабого) закона больших чисел. Используя определение, можно показать, что закон больших чисел эквивалентен слабой сходимости последовательности функций распределения
и найдем в терминах характеристических функций необходимое и достаточное условие для выполнения (слабого) закона больших чисел. Используя определение, можно показать, что закон больших чисел эквивалентен слабой сходимости последовательности функций распределения 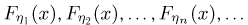 к предельной F(x), представляющей собой функцию распределения случайной величины
к предельной F(x), представляющей собой функцию распределения случайной величины 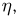 принимающей единственное значение а. Но
принимающей единственное значение а. Но 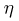 имеет характеристическую функцию
имеет характеристическую функцию 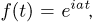 и в силу теоремы непрерывности необходимым и достаточным условием для выполнения закона больших чисел является сходимость
и в силу теоремы непрерывности необходимым и достаточным условием для выполнения закона больших чисел является сходимость 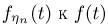 равномерно на любом интервале
равномерно на любом интервале 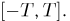 В свою очередь, используя свойства характеристических функций, имеем
В свою очередь, используя свойства характеристических функций, имеем
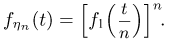
Логарифмируя 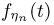 (это можно сделать, поскольку
(это можно сделать, поскольку 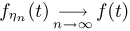 равномерно на любом интервале
равномерно на любом интервале 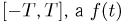 не обращается в нуль), получаем следующее необходимое и достаточное условие:
не обращается в нуль), получаем следующее необходимое и достаточное условие: 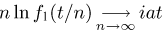 равномерно на любом интервале
равномерно на любом интервале 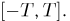 Последнее условие, в свою очередь, эквивалентно условию
Последнее условие, в свою очередь, эквивалентно условию
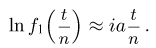
Разлагая логарифм в ряд Маклорена до первого члена, получаем
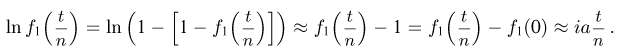
Наконец, полагая 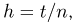 окончательно находим, что необходимым и достаточным условием для выполнения закона больших чисел является существование предела
окончательно находим, что необходимым и достаточным условием для выполнения закона больших чисел является существование предела
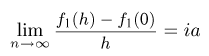
или, иными словами, существование в нуле производной 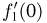 характеристической функции
характеристической функции 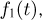 причем постоянная а, фигурирующая в определении закона больших чисел, вычисляется через эту производную по формуле
причем постоянная а, фигурирующая в определении закона больших чисел, вычисляется через эту производную по формуле 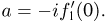
Таким образом, с использованием аппарата характеристических функций нам удалось чрезвычайно просто найти необходимое и достаточное условие выполнения (слабого) закона больших чисел для последовательности независимых одинаково распределенных случайных величин 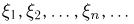
Скажем еще несколько слов о связи слабого и усиленного законов больших чисел. Из свойств характеристических функций следует, что если случайная величина 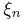 имеет математическое ожидание
имеет математическое ожидание 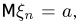 то производная
то производная 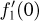 существует и равна
существует и равна 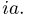 Значит, для последовательности
Значит, для последовательности 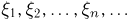 выполнен слабый закон больших чисел и не выполнен усиленный тогда и только тогда, когда
выполнен слабый закон больших чисел и не выполнен усиленный тогда и только тогда, когда 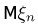 не существует, но тем не менее существует производная
не существует, но тем не менее существует производная 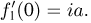
В заключение этого параграфа отметим, что наряду с характеристическими функциями в теории вероятностей используются также преобразования Лапласа-Стилтьеса 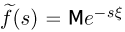 (для неотрицательных случайных величин
(для неотрицательных случайных величин 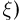 и производящие функции
и производящие функции 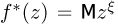 (для неотрицательных целочисленных случайных величин
(для неотрицательных целочисленных случайных величин 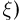 Ясно, что преобразование Лапласа-Стилтьеса
Ясно, что преобразование Лапласа-Стилтьеса 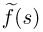 и производящая функция
и производящая функция 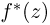 связаны с характеристической функцией той же самой случайной величины соотношениями:
связаны с характеристической функцией той же самой случайной величины соотношениями: 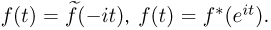 Преобразование Лапласа-Стилтьеса и производящая функция, по сути дела, имеют те же самые свойства, что и характеристическая функция, но с ними существенно проще обращаться уже хотя бы потому, что они являются действительными функциями.
Преобразование Лапласа-Стилтьеса и производящая функция, по сути дела, имеют те же самые свойства, что и характеристическая функция, но с ними существенно проще обращаться уже хотя бы потому, что они являются действительными функциями.
Рассмотрим последовательность независимых одинаково распределенных случайных величин 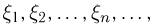 имеющих математическое ожидание
имеющих математическое ожидание 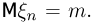 Предположим также, что существует дисперсия
Предположим также, что существует дисперсия 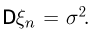 Закон больших чисел для этой последовательности можно представить в следующей форме:
Закон больших чисел для этой последовательности можно представить в следующей форме:
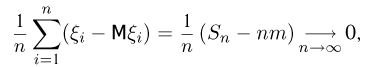
где сходимость можно понимать как в смысле сходимости по вероятности (слабый закон больших чисел), так и в смысле сходимости с вероятностью, равной единице (усиленный закон больших чисел).
Однако сразу же возникает вопрос: поскольку от случайных величин 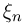 мы потребовали существования не только математического ожидания, но и дисперсии, то нельзя ли получить более «тонкую» предельную теорему, позволяющую точнее описать предельное поведение распределений центрированных сумм
мы потребовали существования не только математического ожидания, но и дисперсии, то нельзя ли получить более «тонкую» предельную теорему, позволяющую точнее описать предельное поведение распределений центрированных сумм 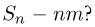 Такая теорема имеется и носит название центральной предельной теоремы. При этом нормировка
Такая теорема имеется и носит название центральной предельной теоремы. При этом нормировка 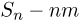 осуществляется величиной
осуществляется величиной 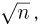 а не п, т.е. последовательностью постоянных, стремящейся к бесконечности медленнее, чем п.
а не п, т.е. последовательностью постоянных, стремящейся к бесконечности медленнее, чем п.
Центральная предельная теорема
Центральная предельная теорема:
Пусть 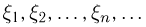 последовательность независимых одинаково распределенных случайных величин,
последовательность независимых одинаково распределенных случайных величин, 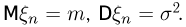 Тогда
Тогда
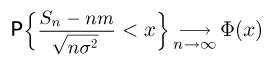
(напомним, что Ф(x) — функция стандартного нормального распределения).
Доказательство:
Прежде всего заметим, что поскольку функция стандартного нормального распределения Ф(x) является непрерывной, то сходимость к ней последовательности функций распределения в каждой точке представляет собой слабую сходимость и, значит, для доказательства центральной предельной теоремы можно воспользоваться теоремой непрерывности. Обозначим через 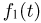 характеристическую функцию случайных величин
характеристическую функцию случайных величин 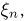 а через
а через 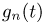 — характеристическую функцию случайной величины
— характеристическую функцию случайной величины 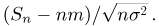 Воспользовавшись теперь свойствами 2 и 3 характеристических функций, имеем
Воспользовавшись теперь свойствами 2 и 3 характеристических функций, имеем
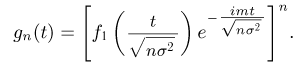
Поскольку 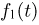 имеет производные первых двух порядков (свойство 4 характеристических функций) то
имеет производные первых двух порядков (свойство 4 характеристических функций) то 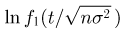 разложить в ряд Маклорена по степеням
разложить в ряд Маклорена по степеням 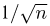 до второго члена:
до второго члена:
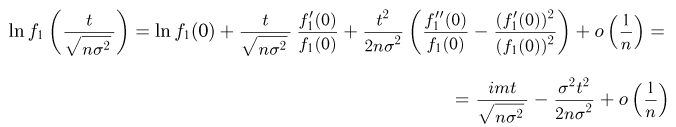
и значит
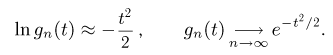
Но 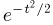 есть не что иное, как характеристическая функция
есть не что иное, как характеристическая функция 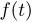 стандартного нормального распределения (см. пример 7). Тем самым завершается доказательство теоремы.
стандартного нормального распределения (см. пример 7). Тем самым завершается доказательство теоремы.
Центральная предельная теорема выявляет ту роль, которую играет нормальное распределение. Оно обычно возникает в явлениях, подверженных большому количеству малых случайных воздействий. Уже само название «нормальный закон» объясняется тем широким распространением, которое он находит на практике в самых различных областях научных исследований.
Пример:
Рассмотрим п испытаний по схеме Бернулли с вероятностью успеха р и вероятностью неудачи 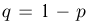 в каждом. Пусть
в каждом. Пусть 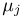 — число успехов в j-м испытании. Тогда
— число успехов в j-м испытании. Тогда 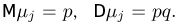 Обозначим через
Обозначим через 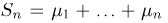 суммарное число успехов в п испытаниях. В силу центральной предельной теоремы с ростом п распределения случайных величин
суммарное число успехов в п испытаниях. В силу центральной предельной теоремы с ростом п распределения случайных величин 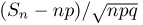 сходятся к стандартному нормальному закону, т.е.
сходятся к стандартному нормальному закону, т.е.
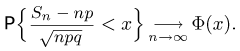
Это утверждение представляет собой не что иное, как интегральную теорему Муавра-Лапласа (см. параграф 3 гл. 4).
Пример:
Для определения скорости  движения объекта выполняется п измерений
движения объекта выполняется п измерений  причем j-e измерение производится со случайной ошибкой
причем j-e измерение производится со случайной ошибкой 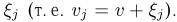 Предполагая, что ошибки измерений
Предполагая, что ошибки измерений 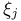 независимы и одинаково распределены с математическим ожиданием
независимы и одинаково распределены с математическим ожиданием 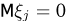 (отсутствуют систематические ошибки наблюдений) и дисперсией
(отсутствуют систематические ошибки наблюдений) и дисперсией 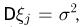 оценим вероятность того, что средняя наблюденная скорость
оценим вероятность того, что средняя наблюденная скорость 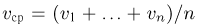 будет отличаться от истинной скорости
будет отличаться от истинной скорости 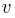 не более чем на
не более чем на 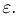 Тогда
Тогда
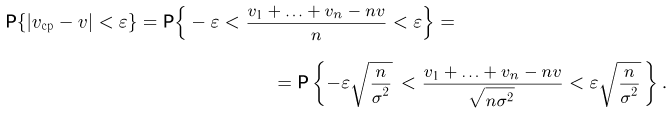
Считая теперь, что число п измерений велико, воспользуемся центральной предельной теоремой, по которой случайная величина 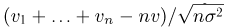 распределена приближенно по стандартному нормальному закону. Значит,
распределена приближенно по стандартному нормальному закону. Значит,
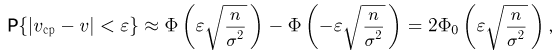
где значение интеграла Лапласа 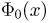 приведено в табл. 3 приложения.
приведено в табл. 3 приложения.
Решение заданий и задач по предметам:
Дополнительные лекции по теории вероятностей:
- Случайные события и их вероятности
- Случайные величины
- Функции случайных величин
- Числовые характеристики случайных величин
- Законы больших чисел
- Статистические оценки
- Статистическая проверка гипотез
- Статистическое исследование зависимостей
- Теории игр
- Вероятность события
- Теорема умножения вероятностей
- Формула полной вероятности
- Теорема о повторении опытов
- Нормальный закон распределения
- Определение законов распределения случайных величин на основе опытных данных
- Системы случайных величин
- Нормальный закон распределения для системы случайных величин
- Вероятностное пространство
- Классическое определение вероятности
- Геометрическая вероятность
- Условная вероятность
- Схема Бернулли
- Многомерные случайные величины
- Оценки неизвестных параметров
- Генеральная совокупность

