Оглавление:




Предельное равновесие пластинок
- Конечное равновесие пластины. Расчет плиты На упругом этапе их работы является предметом прикладной теории упругости, которая выходит за рамки данного курса. Часто, находя такую же верхнюю номинальность пропускной способности плиты сделано мимо. Соответствующая теория построена применительно к расчету бетонных и железобетонных плит и в настоящее время в основном применяется к железобетонным конструкциям. Бетонные плиты
становятся хрупкими с образованием трещин, поэтому соображения, разработанные для идеального пластического материала, не могут быть применены в этом случае. По сути, при формулировании основных принципов ограничения Из идеала-достаточно простой пластик На самом деле, рассмотрение остояние
физических свойств не требует доказательства соответствующей теоремы, и предельное с Людмила Фирмаль
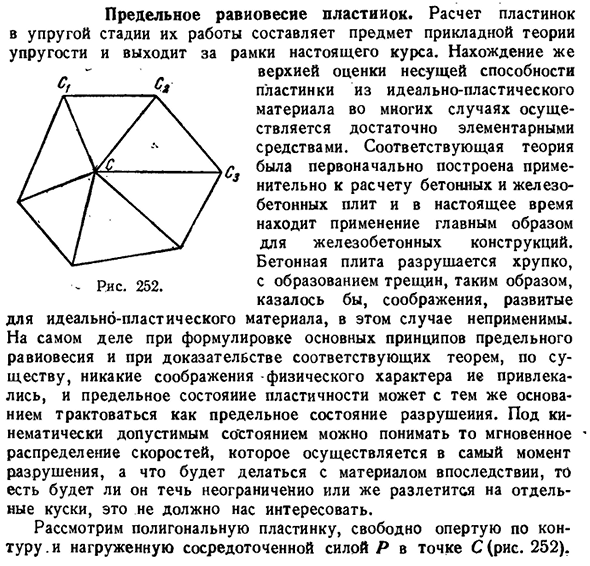
пластичности можно рассматривать по тем же причинам, что и предельное состояние разрушения. Под кинематически допустимыми условиями можно понимать мгновенное распределение скорости, которое осуществляется в момент разрушения, а что делается с материалом позже, то есть определить не представляется возможным. Рассмотрим многоугольную пластину, которая просто опирается по контуру и нагружает точку C фокусом
P(рис. 252), 169] предельное равновесие 367 на пластине Один из возможных кинематических планов разрушения (или пластической деформации) таких пластин заключается в следующем. Вдоль линии, соединяющей точку приложения силы с вершиной контура, происходит излом, плоская центральная поверхность входит в поверхность пирамиды, ее кромка образована линией сверху, грань показывает прогиб в точке приложения силы S, длину кромки
- излома ls, два угла между плоскостями, прилегающими к соответствующей кромке,©j. изгибающий момент на единицу длины линии пробоя равен 2,и рабочее уравнение приводит к следующему уравнению: Чтобы найти двугранный угол (y), проведите прямую AB перпендикулярно линии ls через точку действия силы C(рис. 253), и продолжается сторона контура пластины, примыкающая к вершине Cs до пересечения с прямой AB. Левая часть вращается вблизи прямой линии ACS, как видно из c= / ^f. Прямо рядом с прямым BCS, прямой ACB сломан, на том же рисунке во второй проекции; o под этим углом,. Следовательно, X C= / J tgq)
равно i, И 7J (КГН<Р»+КТГ Кроме уравнения работы, получаем: f>=yw T2 (c tgт-г<р=тг£.368 теория предельного равновесия[гл. XV Предельная нагрузка задается по формуле 2Р£тг 2Это. В) К Р у г л А я п л А с т и Н К А, О П Е Р Т А я на К О Н Т У р у. круглую пластину можно рассматривать как ограниченный случай пластики- Рис, 254. Тонкое, дающее выражение в виде регулярного движения к бесконечности: Многоугольника с несколькими сторонами и многоугольника с таким краевым переходом- P=2 l L4t. Поверхность изогнутой пластины в ее конечном состоянии является конической.
Можно показать, что он эффективен не только кинематически, но и статически. Если Людмила Фирмаль
плита носит равномерно распределенную нагрузку, то npif можно только сделать в таком же путе, для И Чтобы рассчитать работу распределенной нагрузки, силу нагрузки следует умножить на объем пирамиды. Пирамидальная форма разрушения не всегда соответствует минимальной нагрузке. Для пластин, защемленных по контуру, применяя ту же схему разрушения, а не только линию, соединяющую вершину вершины, трещина формируется вдоль запечатанной стороны, соответствующий угол этой стороны равен B/P. 256), работа момента на каждой стороне выражается следующим образом: MTbaJps. J p j s d g i/>, вводя 4-ctg в уравнение, мы видим, что в правой части этого уравнения снова появляется то же выражение, что и раньше, и уравнение принимает вид: P= = 2MT
(169.2)§ 169]конечное равновесие пластины 369. Следующие параметры не определены Для круглой пластины, зажатой по контуру, P=4l L4t. (169.3) в случае полигональной, sum^] (ctg), 4~ctg ipj всегда можно показать, что больше, чем 2l, нагрузка, рассчитанная для диска по уравнению (169.3) пирамидальная схема разрушения пластины, зажатой по контуру к полигональной пластине, такая пластина под действием неправильной концентрации пластины разрывает круг, конический (257). Радиус предельной нагрузки этого круга не зависит от радиуса.
Смотрите также:

