Оглавление:
Рассмотрим определение предела функции при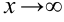 
.
Число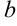 
называется пределом функции 
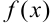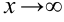при , если для любого наперед заданного 
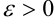существует такое 
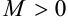, что для всех 
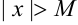имеет место неравенство: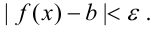 
Если 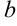есть предел функци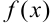и при 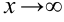, то пишут: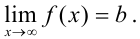 
Поясним смысл определения: какую бы точность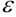 
мы ни задали, найдется число 
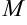, такое, что при выборе 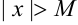, значения функции будут отличаться от 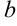на число, меньшее 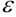(т.е. значения функции практически не будут отличаться от ).
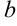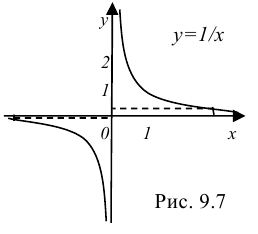
В качестве примера рассмотрим всем хорошо известную функцию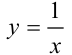 
(рис. 9.7) и покажем, что ее предел при 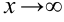равен 0.
Пусть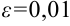 
. Тогда можно подобрать число 
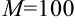, и для всех 
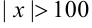модуль разности 
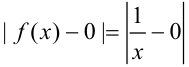будет меньше точности 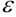. Таким образом, 
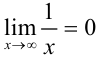. Это согласуется и с нашим наглядным представлением: если выбирать достаточно большие значения 
, значения переменной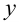 
практически не будут отличаться от 0.
При нахождении пределов функций будем пользоваться двумя основными пределами:
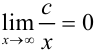и 
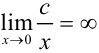, где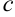 
— константа.
Для вычисления предела дроби при 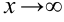будем использовать следующее правило: разделим каждое слагаемое числителя и знаменателя на в наивысшей степени. Возможны три случая:
5.1. наивысшая степень числителя совпадает с наивысшей степенью знаменателя:
Пример №9.6.
Вычислите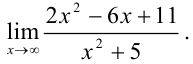 
Разделим каждое слагаемое числителя и знаменателя на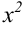 
. Получим:
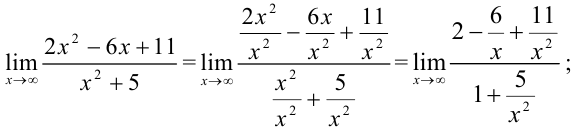
Каждое слагаемое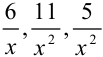 
стремится к 0 при 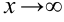, тогда
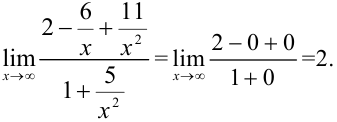
Итак, если наивысшая степень числителя совпадает с наивысшей степенью знаменателя, то в пределе получается число, отличное от нуля.
5.2. наивысшая степень числителя больше наивысшей степени знаменателя:
Пример №9.7.
Вычислите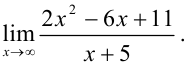 
Разделим каждое слагаемое числителя и знаменателя на 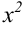. Получим:
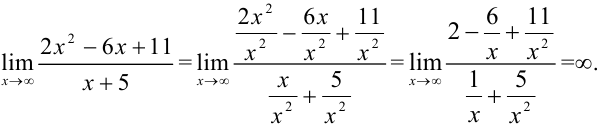
Таким образом, если наивысшая степень числителя больше наивысшей степени знаменателя, то в пределе получается бесконечность.
5.3. наивысшая степень числителя меньше наивысшей степени знаменателя:
Пример №9.8.
Вычислите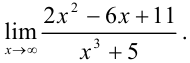 
Разделим каждое слагаемое числителя и знаменателя на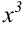 
. Получим:
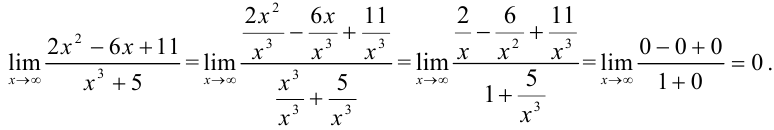
Таким образом, если наивысшая степень числителя меньше наивысшей степени знаменателя, то в пределе получается ноль.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Основные теоремы о пределах функции. |
| Техника вычисления пределов. |
| Замечательные пределы. |
| Непрерывность функции в точке и на промежутке. |
