Поверхности вращения. Тор поверхность.
Поверхность, получаемая при вращении образующей окружности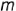 
(или ее дуги) вокруг оси 
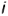, лежащей в плоскости этой окружности, но не проходящей через ее центр, называется торовой.
Образующая окружность 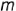вращается вокруг оси тора 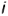по направляющей окружности радиусом 
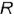(рис. 4.83 а,б,в,г).
Геометрическое тело, ограниченное торовой поверхностью, называю! тором.
Тор называют открытым (круговое кольцо), если образующие окружности 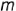в осевом сечении не пересекаются и не касаются друг друга, т.е. 
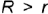. Проекции открытого тора с горизонтально-проецирующей осью вращения 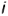показаны на рис. 4.83, а
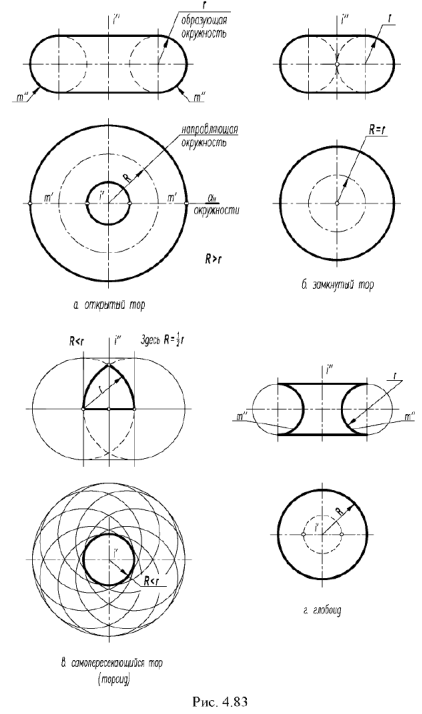
Тор называют замкнутым, если образующие окружности m касаются, т.е.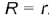 
. Проекции замкнутого тора показаны на рис. 4.83, О.
Тор называют самопересекающимся, если образующие окружности пересекаются, т.е.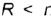 
. Проекции самоперссекающегося тора показаны на рис. 4 83, в. Выделенную часть самопересекающегося тора называют то рои дом и часто используют в графических условиях различных задач.
На рис. 4.83, г показаны проекции глобоида — это геометрическое тело, образованное как открытый тор, но материализующее полость (отверстие) в открытом торе.
Эта теория взята со страницы задач по начертательной геометрии:
Возможно эти страницы вам будут полезны:
