Оглавление:
Поверхности вращения
Поверхностью вращения называют поверхность, образованную вращением некоторой линии (образующей поверхности) вокруг неподвижной прямой, называемой осью вращения. При этом образующая, вращаясь вокруг оси вращения, может пересекать окружность, называемую направляющей поверхности. Образующей поверхности вращения может быть кривая или прямая линия. Поверхность вращения называют линейчатой, если ее образующей является прямая линия, и криволинейной, если образующая — кривая линия.
На рис. 7.5 показана поверхность вращения общего вида, образующая которой (кривая линия) вращается вокруг горизонтально-проецирующей оси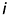 
. Все точки образующей вращаются вокруг оси 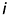по окружностям соответствующего радиуса, которые называют параллелями поверхности. На фронтальную и профильную проекции поверхности эти параллели проецируются в прямые линии, перпендикулярные оси вращения. На горизонтальную проекцию параллели проецируются в виде окружностей. Некоторые параллели имеют определенные общепринятые наименования:
- горло поверхности — параллель наименьшего (минимального) радиуса;
- экватор — параллель наибольшего (максимального)
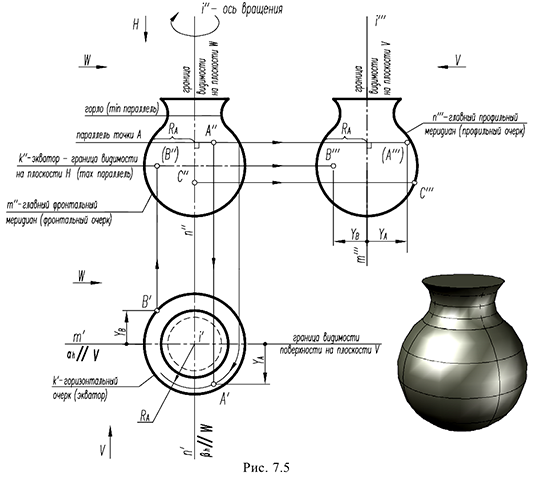
Проекции поверхности вращения:
- горизонтальная проекция, то есть ее горизонтальный очерк, определяется окружностью экватора
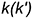; - фронтальная проекция, то есть ее фронтальный очерк, образуется замкнутой линией главного фронтального меридиана
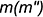, полученного при пересечении этой поверхности фронтальной плоскостью уровня 
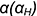, проходящей через ось вращения 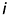; - профильная проекция, то есть ее профильный очерк, образуется замкнутой линией главного профильного меридиана
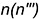, полученного при пересечении этой поверхности профильной плоскостью уровня 
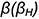, проходящей через ось вращения .
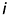Построение проекций точек на поверхности вращения
Принадлежность точки поверхности вращения определяется ее принадлежностью параллели, по которой точка вращается вокруг оси вращения.
Проекции точек, лежащих на экваторе или на главных фронтальном и профильном меридианах поверхности, строятся по их принадлежности этим характерным линиям.
На рис. 7.5 показан пример построения невидимой фронтальной проекции характерной точки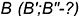 
, лежащей на экваторе 
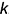, по ее заданной горизонтальной проекции 
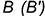и построение профильной проекции характерной точки 
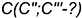, лежащей на главном профильном меридиане 
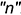, по ее заданной фронтальной проекции.
Для построения проекций точки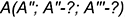 
, заданной своей фронтальной проекцией и не лежащей на характерных линиях поверхности, требуется выполнить следующий графический алгоритм:
1-е действие. Провести через заданную фронтальную проекцию точки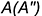 
параллель, которая имеет радиус 
.
2-е действие. Провести на горизонтальной проекции поверхности окружность-параллель радиусом .
3-е действие. Построить по вертикальной линии связи горизонтальную видимую проекцию точки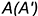 
по ее принадлежности построенной параллели радиусом Ra.
4-е действие. Построить профильную проекцию точки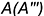 
на горизонтальной линии связи по координате 
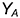(лежит на невидимой части поверхности, проекция взята в скобки).
Видимость точек на проекциях поверхности вращения
На рис. 7.5 показаны границы видимости поверхности для каждой проекции по направлению взгляда на плоскости проекци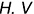й 
и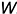 
.
Видимость точек на проекциях поверхности определяется этими границами, то есть видимостью части поверхности на каждой проекции: если часть поверхности является по направлению взгляда на соответствующую плоскость проекций видимой, то точка на этой проекции будет также видимой.
На рис. 7.5 видно, что горизонтальная проекция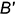 
заданной точки 
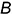, лежащей на экваторе, расположена на невидимой части поверхности при взгляде на фронтальную плоскость проекций 
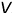. Следовательно, ее фронтальная проекция 
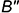лежит на экваторе, но будет невидимой (проекция взята в скобки). Профильная проекция 
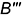точки будет видимой, так как точка лежит на видимой для профильной проекции части поверхности (см. взгляд по стрелке на плоскость 
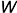). Поскольку заданная фронтальная проекция точки 
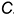, лежащей на фронтальной проекции 
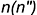главного профильного меридиана, не взята в скобки, значит, она лежит на видимой для фронтальной проекции части поверхности и профильная проекция точки 
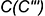должна лежать на профильной проекции главного меридиана 
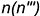справа от оси вращения. Горизонтальная же проекция точки 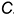(на рисунке не построена) по направлению взгляда на горизонтальную плоскость проекций 
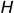будет невидима, так как расположена под экватором. Соответственно профильная проекция точки 
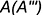будет невидимой, так как лежит на невидимой для профильной проекции части поверхности.
!!! К поверхностям вращения относятся две линейчатые поверхности с прямолинейными образующими — цилиндр и конус, а также поверхности с криволинейными образующими — сфера (образующая — окружность), эллипсоид (образующая — эллипс), одно- и двуполостные гиперболоиды (гипербола), параболоид (парабола), торовые (окружность). Все перечисленные виды поверхностей вращения, кроме торовых, являются поверхностями второго порядка (по порядку образующей или направляющей).
Торовые поверхности вращения относятся к поверхностям четвертого порядка (по произведению порядков двух окружностей — образующей и направляющей).
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Начертательная геометрия для 1 курса
Возможно эти страницы вам будут полезны:
