Задача №120.
Построить планы скоростей и ускорений всех звеньев кривошипно-ползунного механизма (рис. 6.3). Найти линейные скорости и ускорения обозначенных точек и угловые скорости и ускорения звеньев. Линейные размеры звеньев:
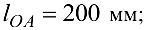
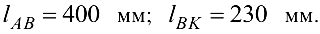
Угловая скорость кривошипа 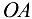
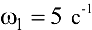 , а ускорение
, а ускорение 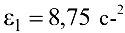 .
.
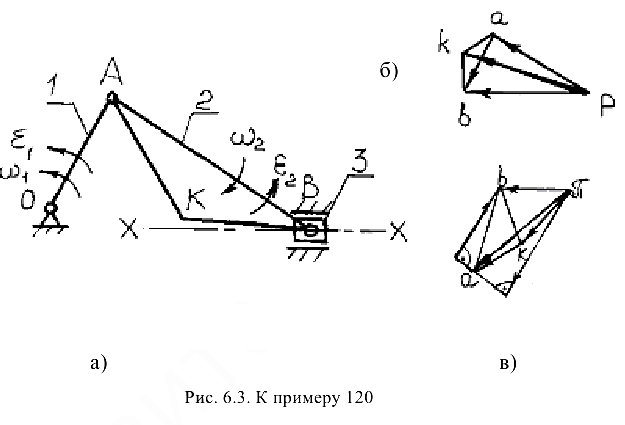
Решение:
Формула строения (0,1) 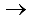 П (2,3) механизм второго класса.
П (2,3) механизм второго класса.
Построение плача скоростей. Скорость точки 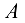 начального звена
начального звена
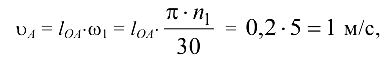
где 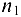 — частота вращения кривошипа
— частота вращения кривошипа 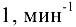 .
.
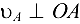 в сторону
в сторону 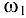 . Выбираем масштабный коэффициент скоростей
. Выбираем масштабный коэффициент скоростей 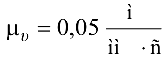 и определяем отрезок
и определяем отрезок 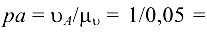
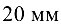 изображающий
изображающий 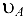 . Точка
. Точка 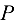 — полюс плана скоростей.
— полюс плана скоростей.
Рассматриваем структурную группу (2, 3). Для определения скорости точки 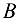 составляем векторное уравнение согласно теореме о плоскопараллельном движении:
составляем векторное уравнение согласно теореме о плоскопараллельном движении:
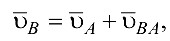
где 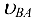 — скорость точки В во вращательном движении звена 2 относительно точки
— скорость точки В во вращательном движении звена 2 относительно точки 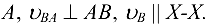
Уравнение (6.9) решаем графически. Для этого из полюса 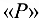 откладываем отрезок
откладываем отрезок 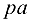 в направлении вектора
в направлении вектора 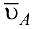 из точки
из точки 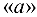 проводим прямую в направлении вектора
проводим прямую в направлении вектора 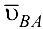 , т. е. перпендикулярно
, т. е. перпендикулярно 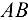 , затем из полюса
, затем из полюса 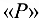 проводим прямую в направлении суммарного вектора
проводим прямую в направлении суммарного вектора 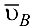 , т. е. параллельно
, т. е. параллельно 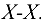 . Пересечение указанных направлений дает точку
. Пересечение указанных направлений дает точку 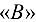 . В результате находим
. В результате находим
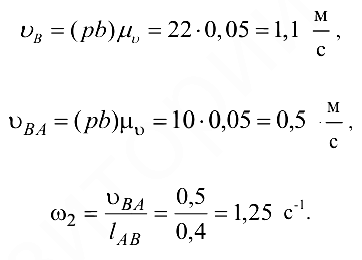
Для определения направления угловой скорости 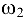 оси шатуна 2 переносим вектор относительной скорости
оси шатуна 2 переносим вектор относительной скорости 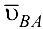 (отрезок
(отрезок 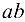 ) в точку
) в точку 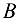 и наблюдаем, в какую сторону он поворачивает звено 2 относительно точки
и наблюдаем, в какую сторону он поворачивает звено 2 относительно точки 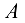 .
.
Скорость точки шатуна 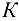 находим на основании векторных уравнений
находим на основании векторных уравнений
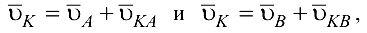
где 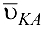 и
и 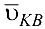 — относительные скорости, причем
— относительные скорости, причем 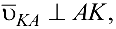
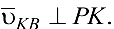
В результате получим
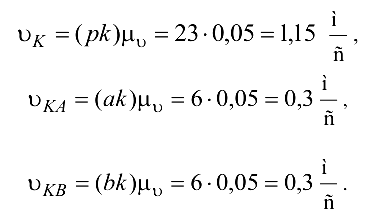
Отметим основные свойства планов скоростей:
- Векторы абсолютных скоростей начинаются в полюсе плана.
- Векторы относительных скоростей соединяют концы векторов абсолютных скоростей, причем вектор на плане направлен к той точке, которая стоит первой в индексе, например,
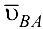 — от
— от 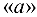 к
к 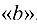 .
. - Теорема подобия: отрезки относительных скоростей точек, принадлежащих одному звену, образуют фигуру, подобную соответствующей фигуре звена и сходственно с нею расположенную. Сходственное расположение означает, что направление обхода одноименных контуров совпадает (например,
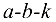 и
и 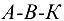 по часовой стрелке). В рассмотренном примере
по часовой стрелке). В рассмотренном примере 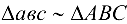 .
.
Построение плана ускорений. Ускорение точки 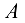 начального звена
начального звена
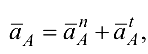
где 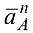 — нормальное ускорение;
— нормальное ускорение;
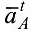 — касательное (тангенциальное) ускорение;
— касательное (тангенциальное) ускорение;
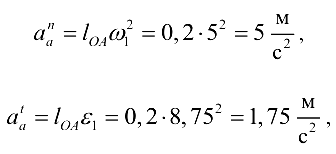
причем вектор 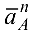 направлен вдоль
направлен вдоль 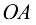 от
от 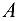 к
к 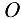 , а
, а 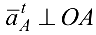 в сторону
в сторону 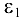 .
.
Выбираем масштабный коэффициент ускорений 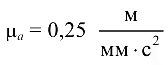 и определяем отрезок
и определяем отрезок 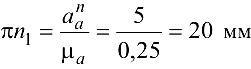 , изображающий
, изображающий 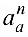 , и отрезок
, и отрезок 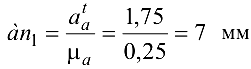 , изображающий
, изображающий 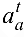 . Точка
. Точка 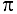 — полюс плана ускорений. Откладываем отрезки
— полюс плана ускорений. Откладываем отрезки 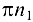 и
и 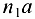 в соответствии с их направлениями. Тогда
в соответствии с их направлениями. Тогда
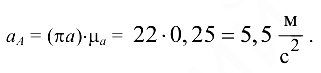
Рассматриваем структурную группу (2, 3). Для определения ускорения точки 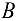 составляем векторное уравнение согласно теореме о плоскопараллельном движении:
составляем векторное уравнение согласно теореме о плоскопараллельном движении:
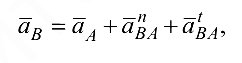
где 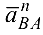 и
и 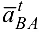 — нормальная и касательная составляющие ускорения
— нормальная и касательная составляющие ускорения 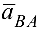 точки
точки 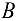 во вращательном движении звена 2 относительно точки
во вращательном движении звена 2 относительно точки 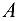 , причем вектор
, причем вектор 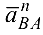 направлен вдоль
направлен вдоль 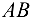 от
от 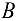 к
к 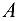 , а
, а 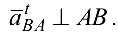 Нормальная составляющая находится также по величине
Нормальная составляющая находится также по величине
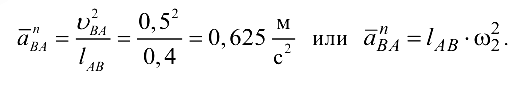
Отрезок, изображающий 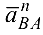 :
:
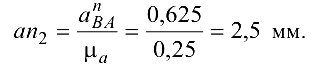
Уравнение (6.10) решаем графически. Для этого из точки 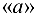 откладываем отрезок
откладываем отрезок 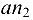 в направлении вектора
в направлении вектора 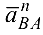 из точки
из точки 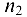 проводим прямую в направлении вектора
проводим прямую в направлении вектора 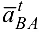 , а из полюса
, а из полюса 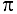 проводим прямую в направлении суммарного вектора
проводим прямую в направлении суммарного вектора 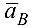 , т. е. параллельно
, т. е. параллельно 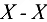 . Пересечение указанных направлений дает точку
. Пересечение указанных направлений дает точку 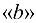 . В результате находим
. В результате находим
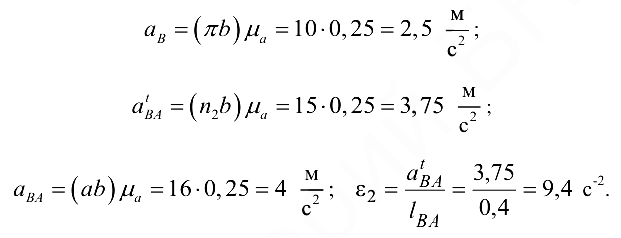
Для определения направления углового ускорения 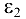 шатуна 2 переносим вектор касательного ускорения
шатуна 2 переносим вектор касательного ускорения 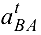 (отрезок
(отрезок 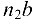 ) в точку
) в точку 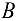 и наблюдаем, в какую сторону он поворачивает звено 2 относительно точки
и наблюдаем, в какую сторону он поворачивает звено 2 относительно точки 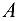 .
.
Ускорение точки 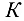 находим на основании теоремы подобия, которая справедлива и для плана ускорений. Для этого методом засечек строим
находим на основании теоремы подобия, которая справедлива и для плана ускорений. Для этого методом засечек строим 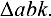 , подобный
, подобный 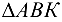 и сходственно с ним расположенный. Стороны
и сходственно с ним расположенный. Стороны 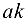 и
и 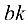 находим из пропорций
находим из пропорций
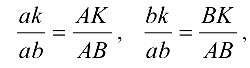
отсюда
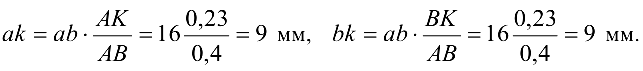
В результате получим
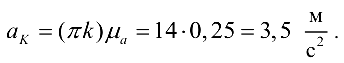
Основные свойства планов ускорений такие же, как и планов скоростей.
Ответ:
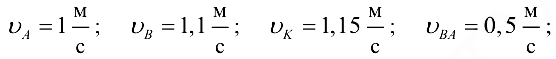
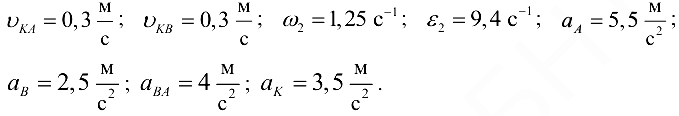
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:

