Построение проекций прямой правильной призмы
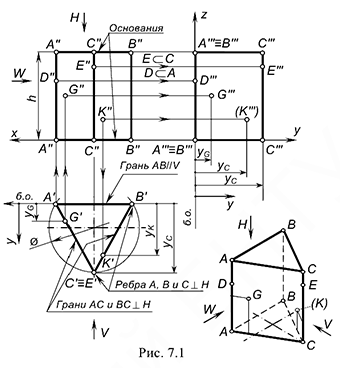
На рис. 7.1 показан пример построения проекций (очерков) прямой правильной призмы высотой 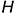 с треугольником в основании, вписанном в окружность заданного диаметра; основания призмы параллельны горизонтальной плоскости проекций
с треугольником в основании, вписанном в окружность заданного диаметра; основания призмы параллельны горизонтальной плоскости проекций 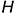 .
.
Для построения проекций призмы требуется выполнить графоаналитические действия в следующем порядке:
1-е действие. Построить горизонтальную проекцию призмы по заданному основанию, которая представляет собой треугольник с обозначенными вершинами 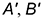 и
и 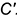 , вписанный в окружность заданного диаметра
, вписанный в окружность заданного диаметра 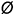 .
.
2-е действие. Выполнить графический анализ построенной горизонтальной проекции призмы:
2.1. Плоскость треугольника 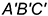 — это горизонтальные натуральные проекции совпадающих параллельных оснований призмы, которые являются горизонтальными плоскостями уровня
— это горизонтальные натуральные проекции совпадающих параллельных оснований призмы, которые являются горизонтальными плоскостями уровня 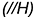 .
.
2.2. Боковые стороны 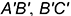 и
и 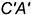 треугольника
треугольника  — это горизонтальные проекции боковых граней призмы, которые спроецировались (выродились) в отрезки прямых линий, так как:
— это горизонтальные проекции боковых граней призмы, которые спроецировались (выродились) в отрезки прямых линий, так как:
- задняя грань
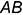 — фронтальная плоскость
— фронтальная плоскость 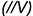 ;
; - передние грани
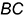 и
и  — горизонтально-проецирующие плоскости
— горизонтально-проецирующие плоскости
2.3. Вершины 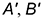 и
и 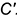 треугольника
треугольника 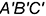 — это горизонтальные проекции ребер, которые спроецировались (выродились) в точки, так как являются горизонтально-проецирующими прямыми
— это горизонтальные проекции ребер, которые спроецировались (выродились) в точки, так как являются горизонтально-проецирующими прямыми 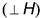 .
.
3-е действие. Построить фронтальную проекцию (очерк) призмы, которая представляет собой прямоугольник, ограниченный:
-по заданной высоте 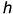 горизонтальными отрезками
горизонтальными отрезками 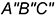 — проекциями оснований
— проекциями оснований 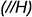 ;
;
- слева — проекцией
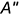 ребра
ребра 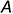 , построенного по вертикальной линии связи;
, построенного по вертикальной линии связи; - справа — проекцией
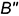 ребра
ребра 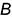 ;
; - фронтальная проекция
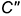 ребра
ребра 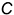 — вертикальный отрезок, совпадающий с осью симметрии фронтальной проекции призмы.
— вертикальный отрезок, совпадающий с осью симметрии фронтальной проекции призмы.
4-е действие. Выполнить графический анализ построенной фронтальной проекции призмы:
4.1. Прямоугольники 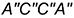 и
и 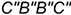 — искаженные проекции передних видимых боковых граней призмы.
— искаженные проекции передних видимых боковых граней призмы.
4.2. Прямоугольник 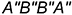 — натуральная величина невидимой задней грани призмы.
— натуральная величина невидимой задней грани призмы.
5-е действие. Построить профильную проекцию (очерк) призмы:
5.1. Задать на горизонтальной проекции призмы положение базовой линии, проходящей через заднюю грань 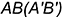 , относительно которой, как от базы отсчета (б.о.), можно определить координату
, относительно которой, как от базы отсчета (б.о.), можно определить координату 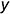 для любой точки на поверхности призмы.
для любой точки на поверхности призмы.
5.2. На поле чертежа справа от фронтальной проекции выбрать положение базовой оси 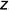 , относительно которой, как от базы отсчета (б.о.), можно построить по координатам
, относительно которой, как от базы отсчета (б.о.), можно построить по координатам 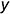 профильные проекции любой точки на поверхности призмы.
профильные проекции любой точки на поверхности призмы.
5.3. Профильная проекция призмы представляет собой прямоугольник, ограниченный:
- по высоте
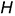 горизонтальными отрезками — проекциями оснований;
горизонтальными отрезками — проекциями оснований; - слева — вертикальным отрезком совпадающих проекций
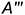 и
и 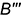 ребер
ребер 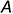 и
и 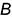 , расположенным на выбранной базовой оси
, расположенным на выбранной базовой оси 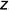 ;
; - справа — вертикальной линией
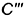 ребра
ребра 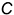 , построенного по координате
, построенного по координате 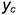 .
.
6-е действие. Выполнить графический анализ построенной профильной проекции призмы.
6.1. Совпадающие прямоугольники 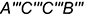 и
и 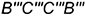 — искаженные проекции передних боковых граней призмы
— искаженные проекции передних боковых граней призмы 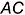 и
и 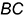 .
.
6.2. Отрезок 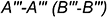 слева — вырожденная проекция задней грани призмы
слева — вырожденная проекция задней грани призмы 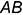 .
.
Построение горизонтальных и профильных проекций точек, лежащих на поверхности призмы
Принадлежность точек поверхности призмы определяется их принадлежностью ребрам и граням этой призмы.
На рис. 7.1 показан пример построения горизонтальных и профильных проекций точек 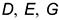 и
и 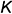 , лежащих на боковой поверхности призмы и заданных фронтальными проекциями:
, лежащих на боковой поверхности призмы и заданных фронтальными проекциями:
- горизонтальные проекции
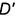 и
и 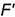 точек
точек 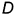 и
и 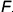 , лежащих на ребрах
, лежащих на ребрах 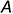 и
и 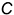 совпадают с горизонтальными проекциями этих ребер — точками
совпадают с горизонтальными проекциями этих ребер — точками 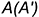 и
и 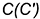 ;
; - горизонтальные проекции
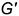 и
и 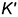 точек
точек 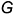 и
и 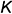 , лежащих на гранях
, лежащих на гранях 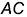 и
и 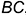 , определяются соответственно на сторонах
, определяются соответственно на сторонах 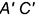 и
и 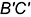 треугольника
треугольника  , которые являются вырожденными проекциями этих граней;
, которые являются вырожденными проекциями этих граней; - профильные проекции точек
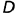 и
и 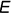 построены по их принадлежности ребрам призмы
построены по их принадлежности ребрам призмы 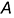 и
и 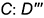 лежит на
лежит на 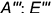 лежит на
лежит на 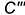 ;
; - профильные проекции точек
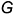 и
и 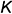 построены по координатам
построены по координатам 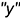 :
: 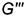 — определяется координатой
— определяется координатой 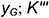 — определяется координатой
— определяется координатой 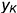 к и на профильной проекции невидима, поскольку лежит на невидимой грани
к и на профильной проекции невидима, поскольку лежит на невидимой грани 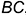 (взята в скобки).
(взята в скобки).
!!! Запомните характерные признаки очерков призмы на чертеже -два прямоугольника и многоугольник основания.
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Начертательная геометрия для 1 курса
Возможно эти страницы вам будут полезны:
| Способ вращения вокруг прямой уровня — горизонтальной или фронтальной прямой |
| Поверхности |
| Построение проекций точек, лежащих на поверхности пирамиды |
| Построение проекций правильной пирамиды |

