Построение проекции тара со срезами плоскостями частного положения
Всякая плоскость пересекает поверхность шара по окружностям (круговым параллелям). В зависимости от расположения секущих плоскостей относительно плоскостей проекций 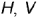 и
и 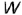 окружности сечений могут проецироваться либо в окружности, либо в эллипсы.
окружности сечений могут проецироваться либо в окружности, либо в эллипсы.
На рис. 4.81 показан пример построения проекций шара со срезами горизонтальной плоскостью 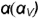 и профильной плоскостью
и профильной плоскостью 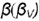 .
.
Окружность сечения шара горизонтальной плоскостью 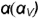 проецируется в окружность (круговую параллель) радиусом
проецируется в окружность (круговую параллель) радиусом 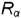 на горизонтальную проекцию шара, а профильная проекции этой окружности — горизонтальная прямая. В качестве оси вращения для построения горизонтальной проекции окружности сечения взята горизонтапьно-проецирующая ось
на горизонтальную проекцию шара, а профильная проекции этой окружности — горизонтальная прямая. В качестве оси вращения для построения горизонтальной проекции окружности сечения взята горизонтапьно-проецирующая ось 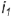 .
.
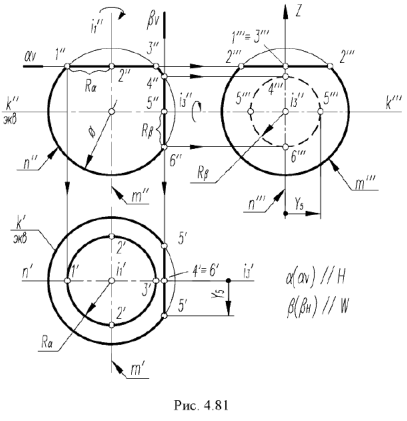
Окружность сечения шара профильной плоскостью 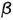 проецируется в окружность (круговую параллель) радиусом
проецируется в окружность (круговую параллель) радиусом 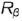 на профильную проекцию шара (невидимая окружность), а горизонтальная проекция этой окружности -вертикальная прямая. В качестве оси вращения для построения параллели
на профильную проекцию шара (невидимая окружность), а горизонтальная проекция этой окружности -вертикальная прямая. В качестве оси вращения для построения параллели 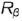 взята профильно-проецирующая ось
взята профильно-проецирующая ось 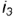 .
.
На этом же рисунке показано расположение проекции характерных точек 7, 2. 3, 4, 5 и б, лежащих в плоскостях сечений на характерных очерковых окружностях шара:
- точки 1, 3. 4 и б лежат на главном фронтальном меридиане шара n и их проекции определяются на проекциях этот меридиана;
- точки 5 лежат на экваторе шара к и их проекции определяются на проекциях экватора;
- точки 2 лежат на профильном меридиане т и их проекции определяются на проекциях этого меридиана.
Оформление очерков проекций ясно из чертежа
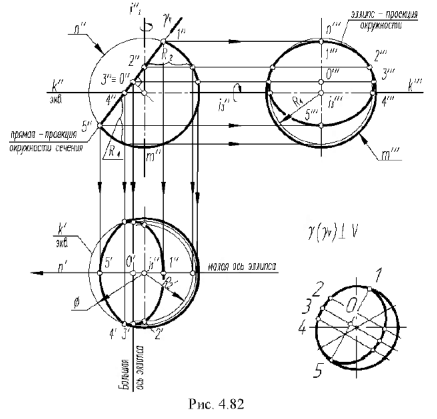
На рис. 4 82 показан пример построения проекций шара со срезом фронтально-проецирующей плоскостью 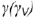 Фронтальная проекция окружности сечения шара плоскостью
Фронтальная проекция окружности сечения шара плоскостью 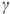 совпадает с вырожденной в линию фронтальной проекцией плоскости
совпадает с вырожденной в линию фронтальной проекцией плоскости 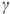 , а на горизонтальную и профильную проекции шара эта окружность сечения проецируется в эллипсы.
, а на горизонтальную и профильную проекции шара эта окружность сечения проецируется в эллипсы.
Проекции шара со срезом построены по проекциям точек, обозначенных на фронтальной проекции сечения.
Горизонтальная проекция шара со срезом в виде эллипса построена по горизонтальным проекциям обозначенных точек:
точки 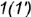 и
и 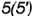 лежат на проекции
лежат на проекции 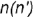 главного фронтального меридиана;
главного фронтального меридиана;
- точки
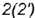 лежат на проекции
лежат на проекции 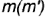 профильного меридиана и построены на параллели радиусом
профильного меридиана и построены на параллели радиусом 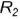 (ось вращения
(ось вращения 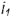 алгоритм I);
алгоритм I);
- точка
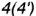 лежит на проекции
лежит на проекции 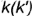 экватора;
экватора; - точки 3 отмечены на перпендикуляре к плоскости сечения у и определяют положение большой оси эллипса 3-3, точки
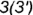 построены но принадлежности своей параллели (алгоритм I); малая ось эллипса — линия
построены но принадлежности своей параллели (алгоритм I); малая ось эллипса — линия 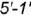 .
.
Построенные видимые горизонтальные проекции точек соединить плавной кривой эллипса с помощью лекала. Очерк горизонтальной проекции определяет ею экватор вправо от точек 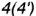 .
.
Профильная проекция шара со срезом в виде эллипса построена по профильным проекциям обозначенных точек:
точки 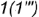 и
и 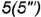 лежат на
лежат на 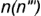 главного меридиана; точки
главного меридиана; точки 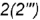 лежат па проекции
лежат па проекции 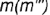 профильного меридиана; точки
профильного меридиана; точки 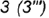 и
и 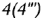 построены или по принадлежности соответствующим относительно оси вращения
построены или по принадлежности соответствующим относительно оси вращения 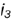 параллелям (алгоритм III, отмечена параллель
параллелям (алгоритм III, отмечена параллель 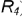 ).
).
Построенные видимые проекции точек соединить кривой эллипса. Очерк профильной проекции определяет профильный меридиан 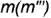 от точек
от точек 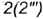 .
.
Эта теория взята со страницы задач по начертательной геометрии:
Возможно эти страницы вам будут полезны:
| Коническая поверхность вращения |
| Построение проекции точек па поверхности шара |
| Поверхности вращения. Тор поверхность |
| Построение проекции открытого тора |

