Построение графика функции

Оглавление:

Построение графика функции

Построение графика функции. Функция^ = F (x) предоставляет x>возможность найти значение функции экстремального значения, что позволяет создать график функции, который точно характеризует ход возрастающих изменений x в интервале[a, b). Ранее в[n°19] были нанесены более или менее плотно взятые точки, но наугад, без учета особенностей графа(ранее неизвестных) ну, с помощью описанного выше метода можно установить определенное количество»опорных»точек, характерных для названия этого графа. Здесь, прежде всего, мы имеем в виду»поворотную точку«графа, то есть вершины вершин и впадины, соответствующие экстремумам функции. ограничьтесь рассмотрением функции y = f (x), принадлежащей классу, обозначенному N°113.

Однако, как правило, все точки должны быть соединены там, где касательные являются горизонтальными или вертикальными, даже если они не соответствуют экстремумам функции. Людмила Фирмаль

Далее, чтобы создать график такой функции y = f (x), нужно сделать следующее: 1) определить значения x, производная y = f ’ ( * ) которых равна нулю или бесконечности (или, по крайней мере, существует бесконечная односторонняя производная) и применить к ним экстремальные значения. 2) вычислить значение функции _y = f ( * ) itself. It соответствует всем этим значениям x и конечным точкам рассматриваемого интервала,% b. Удобно разместить результат в таблице (см. примеры ниже), которая содержит интегральное отображение признаков вычисленных точек графика: максимум, минимум, перегиб, y = 0, y’co, y’ = co И, наконец, Y = zb0 или y ’= q: oo (это произвольный способ показать, существует ли бесконечная односторонность различных знаков).При необходимости добавляются некоторые другие названия графика, например, на пересечении графика и оси.

После прорисовки и вычерчивания всех найденных точек (обычно в небольшом количестве), сам график рисуется через них, с учетом всех вышеперечисленных особенностей. обратите внимание, что в интервале между ними, как описано в ps113, производная держит знак, и график идет намного выше или ниже. если знак x не изменяет значения функции (даже если это функция), то вычисление и кривая упрощаются, а график симметричен относительно вертикальной оси. Аналогичные услуги могут быть предоставлены компанией symmetry в отношении origin. It аналитически выражается в том, что функция меняет знак только тогда, когда изменяется знак x(нечетная функция).

Образцы. 1) функция f ( * ) = 8W * найти экстремум X-xoe^® Создайте ее расписание. Поскольку период действия функции равен 2 суткам, достаточно ограничить его интервалом изменения x[0, 2k].Дериват / ’(л ^ yyy3zt * * * sozlg-38td: * извини, ДГ = 3 $ т х-сох ’ ФПЛ:-sozl). Корни дифференциала (неподвижной точки) в этом случае выглядят так: проходя через x = 0, коэффициент$ 1P x меняет знак минус на плюс, а вся производная меняет знак плюс на минус. Это происходит потому, что последние 2 фактора держат знак минус около x = 0.Есть максимум. Множитель ex * Soz X, когда он исчезает с x=, знак минус превращается в плюс при прохождении через эту точку. Поскольку первые 2 фактора положительны, то же самое относится и к производной. Поэтому и существует мини-Мумм. Остальные стационарные точки изучаются аналогичным образом.

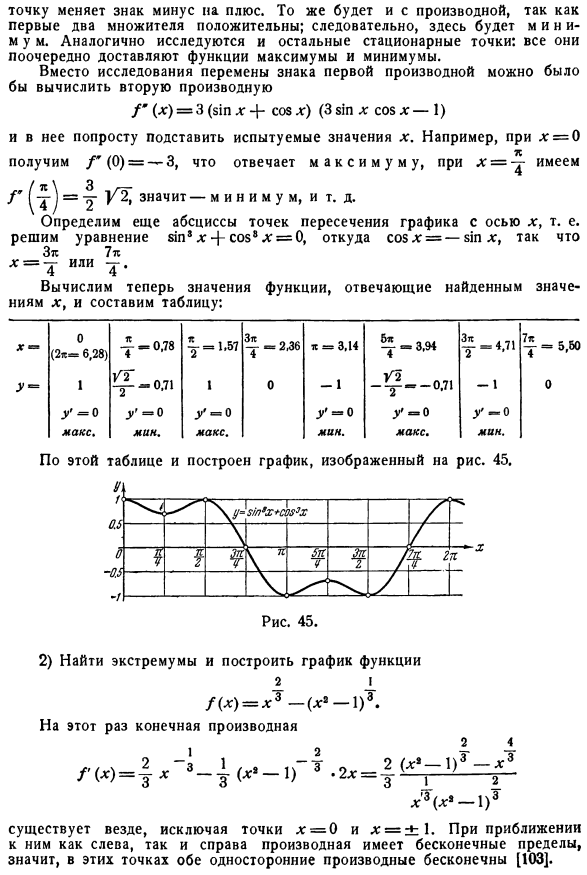
Все они обеспечивают максимальное и минимальное значения функции. Вместо того, чтобы исследовать изменение знака первой производной, мы можем вычислить вторую производную /#(x)= * 3 (ss x 4-ss $ x) (3 ss x ss $ x 1 ss） И просто назначьте ему проверенное значение X. Например, если x = 0, вы получите соответствующее максимальное значение/ «(0)=-3.если x= / ’= y] / 2 / это означает-m и n, m и m и т. д. Он также определяет координаты абсцисс пересечения диаграммы и оси X. То есть мы решаем уравнение an**.|ко $ * * =(), откуда ж $ qр = СР М： X = r или-7 *. 4-4 Затем вычислите значение функции, соответствующее найденному значению x, и составьте таблицу. х■=> 0 （2 *-6.28）* 0.78〜= \。С 4К= 3.14 ^ −3.9 * −471 2 ’^ = 5.60 Г = 1 уг2〜 TG ° ’ 71 1 0 −1 U2 „2“ —0.71 1 0 > ’= 0 г = О Г = О Г-0 г-0 г-0 Макс. минута. максимум. минута. максимум.

График, построенный таким образом-без утверждения точности отдельных ординат-показывает прогресс функции (цель) уже полностью и точно фиксирует интервалы между ее увеличением и уменьшением, а также точку, в которой скорость изменения функции возрастает до нуля или бесконечно. Людмила Фирмаль

Согласно этой таблице, график, показанный на рисунке, равен 45. 2) Найти экстремум и построить график функции 1-я Ф(Х) Х3-(ДГ^® л) 3. На этот раз последний дифференциал / ■()=! 3-4 (*» -!) ’ 3 1 1 х ^ {х ’ −1)3 Т 2., _2(х’-г * Точки * = 0 и x=*±. он существует во всех местах, кроме.Когда вы приближаетесь как влево, так и вправо, производная имеет бесконечный предел. То есть в этих точках производная с одной стороны одновременно бесконечна[103]. Чтобы определить корень производной, сделайте ее молекулу равной нулю. Мы узнаем: л; =±таким образом,»подозрительные» на экстремум Точки： −1〜 УТ ’ 0 ′ ыть ’ 1 Однако, из-за четности функции(отсюда и симметрия графика относительно оси Y).

Максимумы и минимумы. Первое правило.	Использование высших производных.
Максимумы и минимумы. Второе правило.	Разыскание наибольших и наименьших значений.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.