Оглавление:
Построение эпюр внутренних сил в балках способом характерных сечений. Десять (золотых) правил анализа
Этот способ более быстрый. На балке выделяются особые сечения -точки приложения сосредоточенных сил и моментов, начало и конец распределенной нагрузки, места расположения опор, начало и конец балки. Такие сечения следует отметить буквами или пронумеровать слева направо. Отмеченные сечения делят балку на участки. В этих сечениях вычисляются значения внутренних сил и наносятся на эпюры. Полученные точки соединяются с соблюдением очень важных и полезных следующих правил.
- Анализ эпюр всегда выполнять слева направо. При анализе должны выйти из нуля и прийти в ноль.
- В точке приложения сосредоточенного момента на эпюре изгибающих моментов
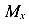наблюдается разрыв (скачок) вниз, если момент направлен по ходу часовой стрелки, и вверх, если он направлен против хода часовой стрелки. - В точке приложения сосредоточенной силы на эпюре поперечных сил
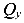наблюдается разрыв (скачок) вниз, если сила направлена вниз, и разрыв (скачок) вверх, если сила направлена вверх. - В точке приложения сосредоточенной силы на эпюре изгибающих моментов 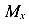наблюдается излом с острием, направленным вниз, если сила направлена вниз, и вверх, если сила направлена вверх.
- Если на участке балки нет распределенной нагрузки q, то поперечная сила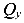на этом участке постоянная, а эпюра изгибающих моментов 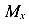имеет прямолинейный характер (линейная).
- На участке балки, где приложена равномерно распределенная нагрузка q, эпюра поперечных сил 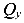имеет прямолинейный характер. Если нагрузка q направлена вниз, то поперечная сила 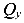уменьшается при движении по балке слева направо, а если вверх, то она увеличивается.
- На участке, где приложена равномерно распределенная нагрузка q, эпюра изгибающих моментов 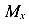имеет вид квадратной параболы с выпуклостью вниз, если q направлена вниз, и вверх, если q направлена вверх.
- В поперечном сечении, где поперечная сила 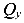равна нулю на эпюре изгибающих моментов
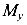наблюдается экстремум. - Площадь эпюры поперечных сил 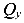на участке балки равна изменению изгибающего момента 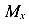на этом участке при условии, что эпюра изгибающих моментов 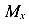не имеет разрыва.
- Если на участке балки поперечная сила 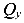положительная, то изгибающий момент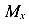увеличивается. И, наоборот.
Отметим, что эти правила справедливы только в случае, если эпюра изгибающих моментов построена на растянутых волокнах балки
Пример:
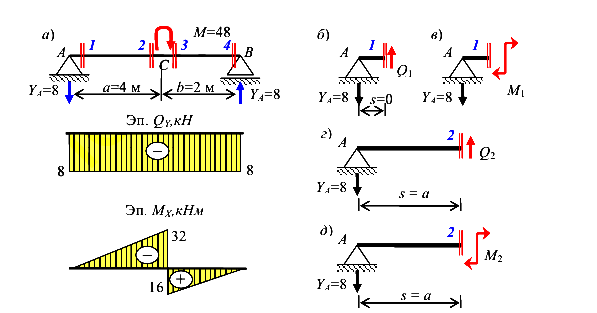
Построения эпюр внутренних сил для элементарной балки методом характерных сечений (рис.49).
момента
Рассмотрим пример, показанный на рисунке (рис.49, а). Вначале, используя уравнения статического равновесия, определим реакции на левой и правой опорах балки. Так как нам заранее неизвестны направления реакций, будем предполагать, что обе реакции направлены вверх. Составим уравнения равновесия.
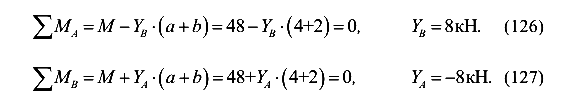
Реакция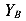 
получилась отрицательной. Это опровергает наши предположения о направлении реакции на левой опоре. Исправим нашу ошибку и направим реакцию 
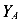вниз (см. рис.49, а).
Рассмотрим часть балки, расположенной слева от сечения 1, к которой приложена единственная внешняя сила 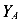, направленная вниз и «пытающаяся» эту часть сдвинуть вниз. Материал сопротивляется такому сдвигу и в рассмотренном сечении появляется поперечная сила 
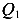направленная вверх и равная реакции 
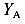(рис.49, б). Обе силы 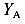и 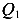вызывают сдвиг, направленный против хода часовой стрелки. Согласно принятому правилу знаков для поперечных сил, поперечная сила 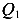принимается отрицательной и равной 
.
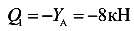Плечо s реакции 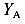стремится к нулю, так как сечение 1 мы провели бесконечно близко к опоре А, располагая его справа (рис.49, б). Поэтому создать момент 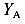не может. Значит, материалу не чему сопротивляться, и изгибающий момент 
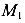равен нулю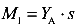 
.
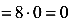Теперь проведем сечение 2 бесконечно близко к точке С слева и рассмотрим левую часть балки от этого сечения (рис.49, в). Повторяется ситуация, полученная для сечения 1. Поэтому и в сечении 2 появиться отрицательная сила равная реакции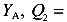 
.
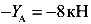Реакция 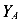имеет плечо относительно сечения 2 и «пытается» повернуть левую часть балки против хода часовой стрелки. Материал сопротивляется и в сечении 2 появляется изгибающий момент 
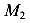, направленный по ходу часовой стрелки. Изображая изгибающий момент в виде пары сил, можно видеть, что верхняя стрелка вызывает растяжение верхних волокон, а нижняя — сжатие нижних волокон. Согласно правилу знаков для изгибающих моментов момент 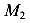принимается отрицательным и равным
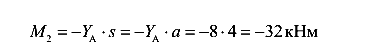
Аналогичными рассуждениями можно найти поперечные силы и изгибающие моменты в сечениях 3 и 4.
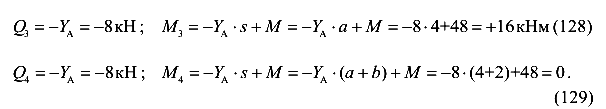
Проверим эпюры поперечных сил и изгибающих моментов, используя десять правил, приведенных выше.
-в точке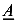 
приложена сосредоточенная сила (реакция 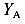) направленная вниз, поэтому на эпюре 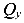наблюдается скачок так же направленный вниз и равный значению ;
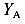-в точке В приложена сосредоточенная сила (реакция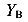 
) направленная вверх, поэтому на эпюре 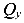наблюдается скачок так же направленный вверх и равный значению 
;
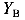-на участке 1-2 нет распределенной нагрузки, поэтому эпюра 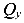постоянна, а эпюра 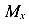имеет прямолинейный характер;
-на участке 1-2 поперечные силы отрицательные, поэтому изгибающие моменты при движении слева направо уменьшаются, при этом изменение изгибающих моментов равно площади эпюры ;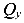
-в точке С к балке приложен сосредоточенный момент М, направленный против хода часовой стрелки, поэтому на эпюре изгибающих моментов наблюдается скачок, направленный вверх;
-на участке 2-3 нет распределенной нагрузки, поэтому эпюра 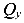постоянна, а эпюра 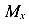имеет прямолинейный характер;
-на участке 2-3 поперечные силы отрицательные, поэтому изгибающие моменты при движении слева направо уменьшаются, при этом изменение изгибающих моментов равно площади эпюры .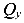
Таким образом, построенные эпюры поперечных и изгибающих моментов соответствуют выше перечисленным правилам. Следовательно, эпюры построены правильно. Построение эпюр методом сечений для балок с более сложной нагрузкой будут рассмотрены на практических занятиях.
Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Решение задач по сопротивлению материалов
Дополнительные страницы которые вам будут полезны:
