Оглавление:






Последовательность расчета статически неопределимых рам методом сил
- Расчет статически неопределенного каркаса осуществляется в следующем порядке: 1) определяется степень статической неопределенности данной системы;2) основная система, число сил и число связей, сброшенных в данном избыточном состоянии, равно степени статической статичности данной системы;3) каноническое уравнение записывается в направлении, которое должно быть равно степени;4) основная система поочередно нагружается силой X=1 и
заданными нагрузками отдельно от каждого удара..»Вычисляются коэффициенты M/и MF для неизвестных и свободных членов канонических уравнений; 6) решается система канонических уравнений, сбрасывается значение неизвестной силы; 7) строится итоговый график с учетом изгибающего момента МОК как сумма единичных графиков M/, а также силы Xj и силы от неизвестной силы. Четыре тысячи сто шесть) Три. Дж Например. График M9q и N в рамке показан на рисунке. 34.6, а. Решение.
Данный кадр статически неопределим, так как SOP=5, W=0,D=1, L=5-3-1=2. Основная система Людмила Фирмаль
выбирается путем опускания горизонтальных и вертикальных опорных стержней опоры В. 34.6, 6). Составим каноническое уравнение из условий равенства нулю горизонтальных и вертикальных перемещений сечения B в основной системе, от действия неизвестных сил, до XY×2.: ++ + Я E2 1\ » + » 2l+d^ = °поскольку все оси g-рам являются прямыми линиями, а жесткость в каждом сечении постоянна, для вычисления смещения b / / и&, правило B^решаги^a (US. 34.6, б-д). Неизвестный фактор: ‘Aljds3’-3-2-3 3-4- 3C
n=J~EJ=2 ~ 3EJ+2EJ 3-3-2-3 36 +2-3EJ~EJ’ . . W3-4-2 3-3-4 30 ОУ=C2i=)Э J-2EJ+2EJ-Эдж:В я ж M22ds 4.4.2-4 4-3-4 _ 58,66 2 2 ~ ^ 4 Джей Джей~2-2 ~ 3EJ+ЭЖ~ЭЖ’ 411^2S Сконфигурируйте общий блок plot=Afi4-Af2(рис. 34.6, д) произвести универсальную проверку точности рассчитанных коэффициентов для неизвестного:+Е22+2 6!2 = 7 7 (36 + 58,66 + 2.30) = ; f A ljd s3-3-2.3 ( 3>4 / 2 — 3 7 \ J EJ » 2-3EJ+4EJ\3)■** 4-3 / 2-4 7\154,66 +2EJ3+3J EJ &1P 9-3-3. 3 9-4-3 Поскольку результаты совпадают, коэффициенты
- неизвестных вычисляются правильно. Рассчитать свободные сроки: Mg Mr ds EJ3-4EJ2EJ 29 \ \ 2.25 3 / EJ’ & 2F 9-4-2 9-3-3-3 9-4 Проверяем найденное значение свободных терминов: 1 206,25 D1R+D2R= ^ 7 (2>25 + 204) = — ~ ; В Г * F-2 1J EJ 7-3 / 2-11 29 \ +2 + \3+3 3EJ Вычисленный канонический свободный член вычисляется правильно. Подставляя в уравнение значения коэффициентов матрицы и свободного члена: 36Xj+30 × 2+2.25=0/30×j+58, 66×2+204=0J. Из решения системы находим значение неизвестного: Xi= = 4,94 кн; x2=-6,003 кн. Предварительное направление выбрано неверно, так как X2 отображается со знаком минус. Фактическая вертикальная реакция направлена вниз. 412
представляет собой график МОК как алгебраическую сумму графика^от заданной нагрузки в основной системе Mr и единицы M2 неизвестной силы x x2, т. е. M0K=_plot MjXi, M2X2 и M2 показаны на рисунке. 34.7, А-В. Проверьте построенный участок МОК. Поскольку узел D и узел E находятся в равновесии, статические проверки выполняются. Кинематический тест. Умножьте МОК на М2 и рассчитайте смещение горизонтальных и вертикальных опор. Это отрезок треугольника и параболы, равный средней ординате (<?/2)/8= (2-32)/8=2,25. 2-2, 25-3 1,5 3. 5,82-3-3.2 2-3£7 +
Ошибка только, но сюжет МОК построен правильно. 0.069 ЭДЖ» До 0,069-100 — =0,08%, Людмила Фирмаль
следователи -‘ 413 на каждый стержень рамы наносят поперечную силу, однопролетную балку (фиг. 34.8). Род БД. Этот стержень оснащен заданной равномерной распределенной нагрузкой(?=2кн/м, а правый опорный момент равен 5,82 кН-м(рис. 34.8, а). Находим эталонную реакцию: 2L4V=^3-1, 5-5, 82-I^Z=O, HD=1,06 кн;=YAV-3 — 2.3.1,5 — 5,82 = 0, ЯВ=4,9 4кн. Согласно этим данным, участок Q строится на стержне BD(рис. 34.8, а). Род де. Этот стержень имеет левый опорный момент 5,82 кН-м и левый опорный момент 18,19 кН-м(рис.Нагруженный с правым вращающим моментом справки. 34.8, 6). Найдите эталонную реакцию: ZMD=5,8 2 + 18,19 — re 4=0, re=6,003 кн;=_R d+R e=0, R d=6,003 кн. График стержня DE Q показан на рисунке. 34.8 б Стержень, с соавт. Поскольку этот стержень не имеет внешней нагрузки, его можно
использовать слева при 1,81 кН-м, а справа при 4,99 кН-м(рис. 34.8, в). Найдите опорный ответ: RMT=нет-3 + 1 ,8 1 — 4,99 = 0, not=1,06 кн; ZZ=H E-HT=0t I g=1,06 кн. График Эт стержня показан на рисунке. 34.8, В. Ядро ЕС. Этот стержень является статически определяемой частью рамы, т. е. консолью, которая нагружается на конце сосредоточенной силой F=10kN. График Q на консоли постоянен и равен 10kN. Окончательный график Q в данном кадре показан на рисунке. 34,8 г Чтобы построить график вертикальных сил, сначала вырежьте узел D, где сходятся два стержня DB и DE(рис. 34.9, а). Боковые силы Qdb и Qde прикладываются к этому узлу с учетом его признаков.
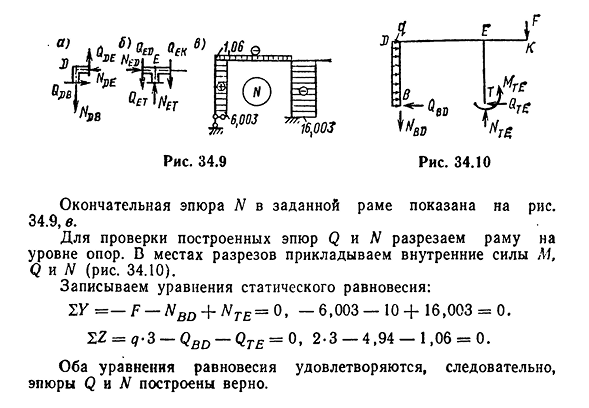
(Положительная боковая сила поворачивает узел в направлении часовой стрелки относительно ее центра). Из уравнения равновесия,=6,093-N d b=0, N d b=6,003 кн; S Z=l, 06+ / VD e=0,/VD E=-1,06 кн. Вырежьте эти узлы E, в которых сходятся три стержня ed, ET и EC(рис. 34.9, 6). В этом узле мы применяем боковых сил, что и требовалось доказать, Щ Э, Qek, с учетом их знаков, и N Эд=н де=-1,06 кн. Из уравнения равновесия следует, что SY=6,003-10-N e t=0, I=G=-16,003 кн. SZ=1,06-1,06+N e k=0, N e k=0. 4143 34.9 рис. 34.10 ^Внутренний Окончательный график N данного кадра показан на
рисунке. 34.9, В. Чтобы проверить построенный участок Q и W, вырежьте рамку на уровне опоры. В месте разреза приложите внутренние силы M, Q, W(рис. 34.10). Напишите уравнение статического равновесия: ZY= — F-NBD+N T E=Q, — 6,003 — 10+ 16,003 = 0. 2Z=q-3-QBD-Qte=G,2.3 — 4,94 — 1,06 =0. Оба уравнения выполнены, и график Q и N построены правильно.
Смотрите также:
Примеры решения задач технической механике
Если вам потребуется помощь по технической механике вы всегда можете написать мне в whatsapp.

