Понятие равномерной непрерывности

Понятие равномерной непрерывности

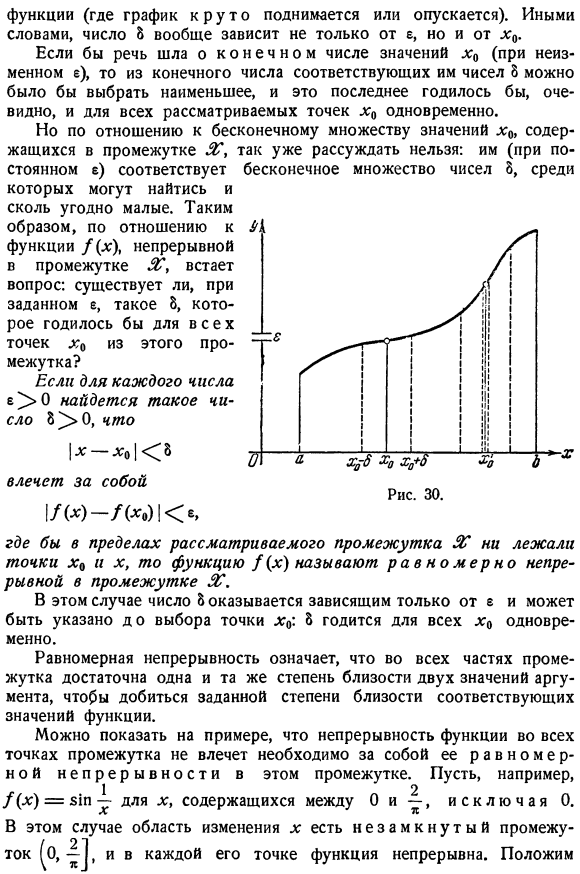
Понятие равномерной непрерывности. Если функция f (x) определена некоторым интервалом k (замкнутым или нет, конечным или бесконечным) и непрерывна в точке π0 этого интервала、 Иш / с )= /( о） Х ♦ * о Или («на языке е-8», n°60): для каждого числа е]> 0 существует такое число, как: \ х— * 0 | 8 импликация| /(ЛГ) / с * о) Ке * Предположим, что функция f (x) непрерывна на всем интервале, то есть непрерывна во всех точках x0 этого интервала. Тогда для каждой точки От^До^для конкретного е существует соответствующая 8 в указанном выше смысле. Когда X изменяется, число 8 является, как правило, изменяется, даже если E является неизменным.

Но мы не можем обсуждать этот метод по отношению к бесконечному множеству значений x0, содержащихся в промежутке. Людмила Фирмаль

• Достаточно, чтобы убедиться, что число 8, которое подходит для области, где функция изменяется медленно(где график представляет собой плавную кривую), слишком велико для области, которая изменяется быстро. Функция(график внезапно поднимается или опускается).То есть число&обычно зависит не только от e, но и от x0. Если речь идет о значениях конечного числа x9 (константы e), то мы можем выбрать из 8 конечных чисел, соответствующих им, наименьшее. Это последнее явно подходит для всех рассматриваемых пунктов одновременно. ZR: они соответствуют бесконечному множеству чисел 8 (в константе e).

• Так что относительно функции f (x), которая непрерывна в интервале. Вопрос: для данного e существует ли подходящая 8 для всех точек в этом интервале? Для каждого числа e> 0, если существует число 8 ^> 0、 \ сопровождающий x-AG0 / Sa ！/（）-/（•）1 л Если точки Xa и x находятся в пределах рассматриваемого интервала GC, то функция/(x) вызывается равномерно и последовательно в пределах интервала. В этом случае получается, что число 8 зависит только от e, и его можно указать перед выбором точки x>.8 подходит для всех x $одновременно.

Равномерная непрерывность означает, что во всех частях интервала одинаковая степень близости двух значений аргумента достаточна для достижения заданной близости соответствующих значений функции. Людмила Фирмаль

• В качестве примера мы можем показать, что непрерывность функции во всех точках промежутка не обязательно требует равномерной непрерывности в этом промежутке. Например、 F (x)=$ ln-r в xy, кроме 0 до 0. Д, Л. В этом случае переменная площадь x-это интервал, который не замкнут(o, > 1, и в каждой точке функция непрерывна. 2 1 * Теперь x9 тогда Джи?. | h. dg= -, где n-любое натуральное число. (2л +1) п * л * /(* 0)= $ ш(2л+ 1）^-=±1、/（。)= $ тлл = 0、 Как это ！/（）-/（*•）1 = 1。 | х-G0 и | n ^ л ^ л Сделайте его сколь угодно маленьким. Где e = 1, 8 не найдено ^ 0, хотя он подходит для всех точек^x $одновременно、 Благодаря непрерывности функции, для каждого отдельного значения x существует такая 8!

Смотрите также:

Решение задач по математическому анализу

Теорема об ограниченности функции.	Теорема о равномерной непрерывности.
Наибольшее и наименьшее значения функции.	Задача о вычислении скорости движущейся точки.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.