Оглавление:
Пусть на 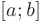 задана непрерывная функция
задана непрерывная функция 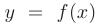 . Разобьем отрезок
. Разобьем отрезок 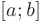 точками
точками 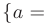
 на
на 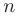 элементарных отрезков
элементарных отрезков 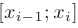 . Тогда, обозначив длину элементарных отрезков как
. Тогда, обозначив длину элементарных отрезков как 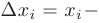
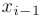 и выбрав на этих отрезках произвольные точки
и выбрав на этих отрезках произвольные точки 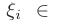
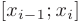 можно составить для функции
можно составить для функции 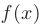 так называемую интегральную сумму:
так называемую интегральную сумму:
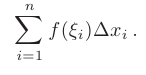
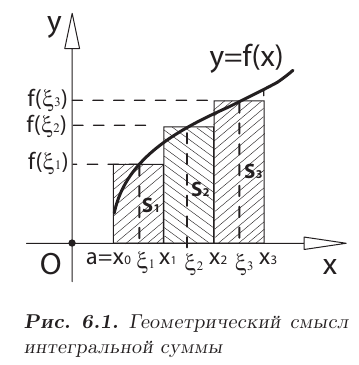
Геометрический смысл интегральной суммы. Пусть 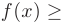 0 на
0 на 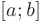 . Каждое слагаемое
. Каждое слагаемое 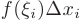 интегральной суммы равно площади
интегральной суммы равно площади 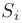 прямоугольника со сторонами
прямоугольника со сторонами 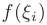 и
и 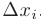 . Поэтому интегральная сумма равна сумме площадей всех прямоугольников
. Поэтому интегральная сумма равна сумме площадей всех прямоугольников 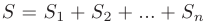 (рис. 6.1).
(рис. 6.1).
Определенным интегралом от функции 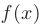 на отрезке
на отрезке 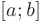 называется предел ее интегральной суммы при длине наибольшего из отрезков стремящейся к нулю
называется предел ее интегральной суммы при длине наибольшего из отрезков стремящейся к нулю 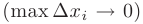 , если этот предел существует, конечен и не зависит от способа разбиения отрезка
, если этот предел существует, конечен и не зависит от способа разбиения отрезка 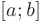 на элементарные отрезки и выбора точек
на элементарные отрезки и выбора точек 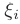 . Формально этот факт обозначается следующим образом:
. Формально этот факт обозначается следующим образом:
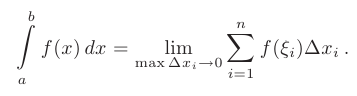
Числа 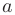 и
и 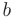 называют нижним и верхним пределами интегрирования. Из приведенного определения следует, что определенный интеграл зависит от вида подынтегральной функции
называют нижним и верхним пределами интегрирования. Из приведенного определения следует, что определенный интеграл зависит от вида подынтегральной функции 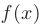 и значений пределов интегрирования
и значений пределов интегрирования 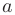 и
и 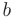 , но не зависит от выбора переменной интегрирования:
, но не зависит от выбора переменной интегрирования:
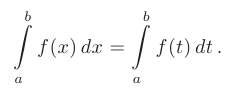
Геометрический смысл определенного интеграла
Если 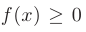 на
на 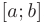 , то
, то 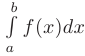 численно равен площади под кривой
численно равен площади под кривой 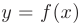 на
на 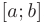 (см. рис. 6.1). Действительно, при
(см. рис. 6.1). Действительно, при 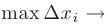 0 ломаная, образованная на каждом из отрезков
0 ломаная, образованная на каждом из отрезков 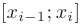 прямой
прямой 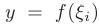 параллельной оси
параллельной оси 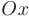 , неограниченно приближается к кривой
, неограниченно приближается к кривой 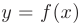 . Площадь под ломаной переходит в площадь под кривой.
. Площадь под ломаной переходит в площадь под кривой.
Свойства определенного интеграла
- Постоянный множитель
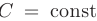 можно выносить за знак определенного интеграла:
можно выносить за знак определенного интеграла:
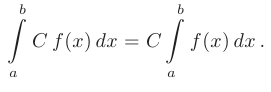
- Определенный интеграл от алгебраической суммы нескольких функций равен алгебраической сумме определенных интегралов от каждого из слагаемых:
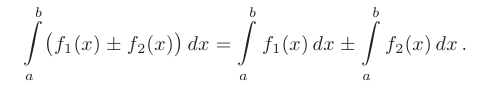
- При перемене мест верхнего и нижнего пределов знак определенного интеграла меняется на противоположный:
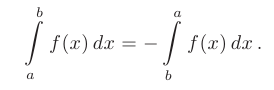
- При совпадении верхнего и нижнего пределов значение определенного интеграла равно нулю:
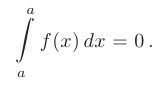
- Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т.е. при любых
 :
:
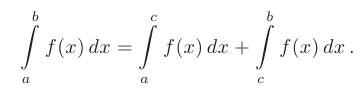
- Если для двух функций на отрезке
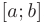 верно неравенство
верно неравенство 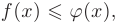 , то такое же неравенство будет верно и для определенных интегралов от этих функций:
, то такое же неравенство будет верно и для определенных интегралов от этих функций:
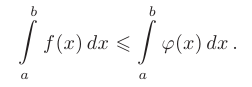
- Если функция
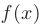 непрерывна на отрезке
непрерывна на отрезке 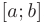 , то на этом отрезке найдется хотя бы одна точка
, то на этом отрезке найдется хотя бы одна точка 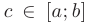 . для которой будет справедливо равенство:
. для которой будет справедливо равенство:
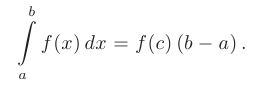
Вычисление определенного интеграла
Вычисление определенных интегралов как предела интегральной суммы часто затруднительно и значительно упрощается, если использовать формулу Ньютона-Лейбница. Если 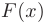 — первообразная для непрерывной на
— первообразная для непрерывной на 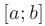 функции
функции 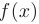 , то определенный интеграл от этой функции
, то определенный интеграл от этой функции 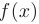 равен приращению любой ее первообразной
равен приращению любой ее первообразной 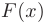 на этом отрезке, т.е.:
на этом отрезке, т.е.:

Как и в случае неопределенного интеграла использование замены переменной позволяет упростить интеграл, приблизив его к табличному. При этом нет необходимости возвращаться к исходной переменной интегрирования, а следует найти пределы интегрирования для новой переменной.
Если функция 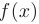 непрерывна на отрезке
непрерывна на отрезке 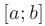 , а функция
, а функция 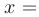
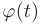 непрерывно дифференцируема на отрезке
непрерывно дифференцируема на отрезке 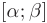 , причем
, причем 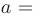
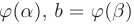 . Тогда справедлива формула замены переменной в определенном интеграле:
. Тогда справедлива формула замены переменной в определенном интеграле:
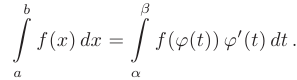
Если функции 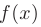 и
и 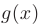 имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке 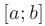 , то справедлива формула интегрирования по частям в определенном интеграле:
, то справедлива формула интегрирования по частям в определенном интеграле:
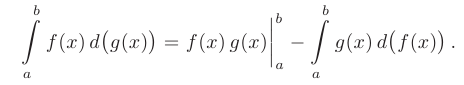
Пример:
Вычислить определенный интеграл с помощью формулы Ньютона-Лейбница
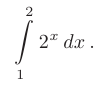
► Произвольная первообразная для функции 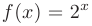 имеет вид:
имеет вид:
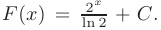
При вычислении по формуле Ньютона-Лейбница возьмем такую первообразную, у которой константа интегрирования равна нулю: 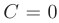 . В результате получим:
. В результате получим:
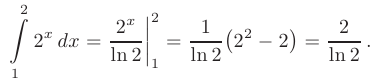
Пример:
Вычислить определенный интеграл методом замены переменной
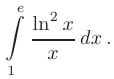
► Заметим, что множитель 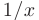 представляет собой производную функции натурального логарифма. Поэтом}’ используя замену переменной вида
представляет собой производную функции натурального логарифма. Поэтом}’ используя замену переменной вида 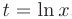 , вычислим ее дифференциал
, вычислим ее дифференциал
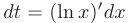
и выполним их подстановку в подынтегральное выражение:
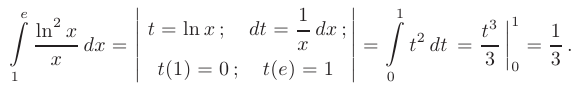
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Интегрирование рациональных дробей в математике |
| Интегрирование иррациональных функций в математике |
| Понятие о несобственных интегралах в математике |
| Вычисление площади плоской фигуры в математике |

