Пусть функция  определена на отрезке
определена на отрезке  .
.
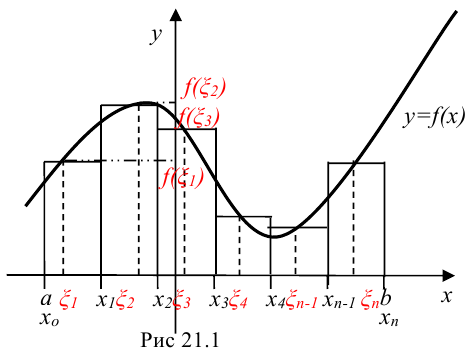
Выполним следующие действия (рис. 21.1).
- С помощью точек
 ,
, 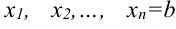 разобьём отрезок
разобьём отрезок 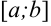 на
на 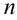 частей
частей 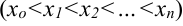 . Длину первого отрезка обозначим
. Длину первого отрезка обозначим 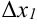 , второго —
, второго — 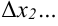 ,
, 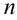 -го —
-го — 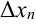 .
. - Внутри каждого отрезка
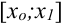 ,
, 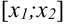 …
… 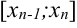 выберем соответственно произвольные точки
выберем соответственно произвольные точки 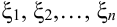 .
. - Найдем значения функции в точках
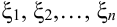 :
: 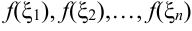 .
. - Для каждого промежутка умножим найденное значение функции
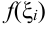 (где
(где 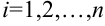 ) на длину соответствующего отрезка
) на длину соответствующего отрезка 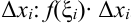 .
. - Составим сумму
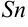 всех таких произведений:
всех таких произведений: 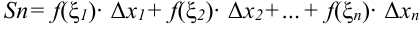 . Эту сумму можно записать в виде:
. Эту сумму можно записать в виде: 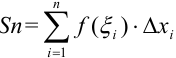 . Такую сумму называют интегральной суммой функции
. Такую сумму называют интегральной суммой функции 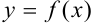 на отрезке
на отрезке 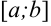 .
.
Если на отрезке 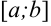 функция
функция 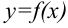 принимает неотрицательные значения, то каждое слагаемое интегральной суммы равно площади прямоугольника с основанием
принимает неотрицательные значения, то каждое слагаемое интегральной суммы равно площади прямоугольника с основанием 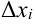 и высотой
и высотой 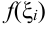 . А вся сумма
. А вся сумма 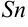 равна площади «ступенчатой фигуры», получающейся объединением рассматриваемых прямоугольников.
равна площади «ступенчатой фигуры», получающейся объединением рассматриваемых прямоугольников.
Мы разбивали отрезок 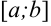 на произвольное число частей, точку
на произвольное число частей, точку 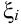 внутри каждого отрезка также выбирали произвольно. Очевидно, что при различных разбиениях отрезка
внутри каждого отрезка также выбирали произвольно. Очевидно, что при различных разбиениях отрезка 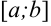 на части и различном выборе точек
на части и различном выборе точек 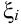 можно составить бесконечное число интегральных сумм.
можно составить бесконечное число интегральных сумм.
Найдем предел интегральной суммы 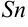 при
при 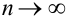 , но при условии, что длина самого большого среди отрезков
, но при условии, что длина самого большого среди отрезков 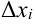 (
(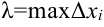 , где
, где 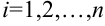 ) будет стремиться к нулю, т.е.
) будет стремиться к нулю, т.е. 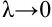 .
.
Если при 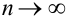 и
и 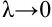 интегральная сумма
интегральная сумма 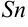 имеет предел
имеет предел 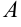 , который не зависит ни от способа разбиения отрезка
, который не зависит ни от способа разбиения отрезка 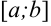 на части, ни от выбора точек
на части, ни от выбора точек 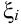 , то число
, то число 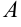 называется определенным интегралом от функции
называется определенным интегралом от функции  на отрезке
на отрезке 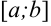 и обозначается
и обозначается 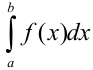 .
.
Таким образом, 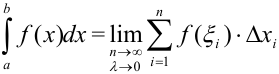 .
.
Числа 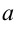 и
и 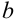 называются соответственно нижней и верхней границами интегрирования.
называются соответственно нижней и верхней границами интегрирования.  — подынтегральной функцией,
— подынтегральной функцией, 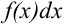 — подынтегральным выражением,
— подынтегральным выражением, 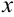 — переменной интегрирования, отрезок
— переменной интегрирования, отрезок 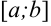 — областью (отрезком) интегрирования.
— областью (отрезком) интегрирования.
Функция  , для которой на отрезке
, для которой на отрезке 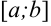 существует определенный интеграл, называется интегрируемой на этом отрезке.
существует определенный интеграл, называется интегрируемой на этом отрезке.
Сформулируем теорему существования определенного интеграла.
Теорема (Коши). Если функция 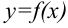 непрерывна на отрезке
непрерывна на отрезке 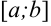 , то определенный интеграл
, то определенный интеграл 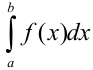 существует.
существует.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Интегрирование некоторых иррациональных функций. |
| Универсальная тригонометрическая подстановка. |
| Основные свойства определенного интеграла. |
| Формула Ньютона-Лейбница. |
