Понятие кривизны

Понятие кривизны

Понятие кривизны. Рассмотрим дугу кривой без множественных особенностей, определяемых параметрическим уравнением * = Р(0. г = ц0-(!） Если в каждой точке нарисована касательная (например, в положительном направлении), кривизна кривой заставляет эту касательную вращаться вместе с движением точки касания. Эта кривая сильно отличается от прямой линии, в которой касательная (соответствующая ей) сохраняет одинаковое направление для всех точек. Важным элементом, характеризующим течение кривой, является «кривизна» или «кривизна» кривой в различных точках. Эта кривизна может быть выражена в виде числа. MMg (рисунок 105) это дуга кривой.

Естественно, кривизна кривой характеризуется углом поворота касательной, рассчитанным для каждой единицы длины дуги. Людмила Фирмаль

• Рассмотрим, что касательные M T и Tx > нарисованы(в положительном направлении В конце этой дуги. 、 То есть, угол W Измеренная в радианах, длина а измеряется в единицах выбранной длины. Это отношение называется средней кривизной дуги кривой. В разных частях кривой, в общем случае, их средняя кривизна различна. Однако существует (уникальная) кривая, где средняя кривизна везде одинакова: круг*).Правда, для нее мы имеем(рис. 106） ■> Девять 1 Мы будем говорить о дуге круга. Из понятия средней кривизны дуги мм \переходят к понятию кривизны в определенной точке. Кривизна кривой в точке M равна、 Средняя кривизна дуги MMX, когда точка Mx вдоль кривой переходит в M.

Если кривизна кривой в данной точке обозначена буквой&、 Л = Тю -. Для окружности, очевидно, k=^ -, то есть кривизна окружности равна Обратная величина радиуса окружности. Замечания. Понятие средней кривизны и кривизны в определенных точках полностью аналогично понятию средней скорости и скорости в определенные моменты времени точки movement. It можно сказать, что средняя кривизна характеризует среднюю скорость изменения направления касания определенной дуги, а кривизна в определенной точке является истинной скоростью изменения этого направления, ограниченной данной точкой. * ) Конечно, прямая линия, в которой кривизна всегда равна нулю, это другое. Далее обратимся к выведению аналитической формулы кривизны.

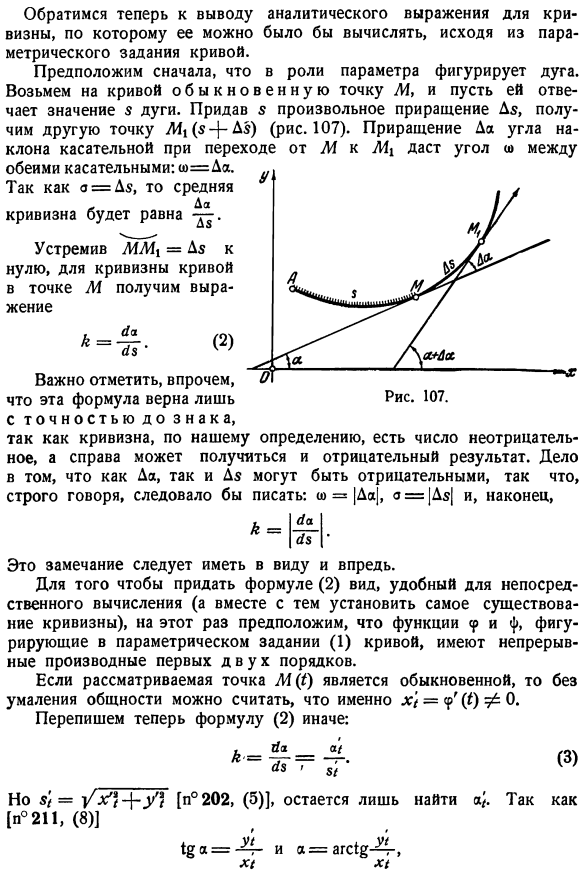
• Согласно этой формуле, она может быть рассчитана на основе параметрических характеристик кривой. Арка. Ответ Половина. Во-первых, предположим, что в качестве параметра он появится, возьмем обычную точку M на кривой и дадим нам знать значение 5 дуг. Дал любое приращение D $до 5, Так каковы же другие точки MD! /D5) (рис.107). Приращение наклона касательной при переходе от M к Mx дает угол между обеими касательными>: w =yes. o = D$, поэтому среднее значение Да. Кривизна будет равна Когда MM \ = D5 указывает на ноль, мы получаем следующее уравнение для кривизны кривой в точке M: (2） А-4!。

В нашем определении кривизна является неотрицательным числом, потому что с правой стороны вы получаете отрицательное число result. In практика, как да, так и D $могут быть отрицательными, поэтому, строго говоря, вам нужно написать w = | Yes|, a = | D5|.И напоследок И Это замечание следует иметь в виду в будущем. Чтобы сделать уравнение (2) удобной формой для прямого вычисления(и одновременно установить существование кривизны), предположим, что функция (лист, который появляется в определении параметра (1) кривой, имеет непрерывную производную Первого 2-го порядка). Если рассматриваемая точка$ ()) нормальна, то можно считать, что она x \ =(p ’() Φ0, не теряя своей общности.

Однако важно отметить, что это выражение верно только до знака. Людмила Фирмаль

• Перепишите выражение (2) другим способом. (3） д / Пять / Но остается только найти[n°202, (5)], а).С (n°211, (8）] * * * {ОБРАТНЫЙ ОСМОС. = С-и = agc1& ->-、 XI X { (4 )） (3) подставьте значение и a для достижения конечного выражения. (5） Эта формула вполне подходит для расчета. Потому что все производные, которые появляются в этом уравнении, просто вычисляются параметрическими уравнениями кривой. Если кривая задана явным уравнением y = f (x), то эта формула принимает вид: (5а） (1 + .y; «） /»• Наконец, учитывая полярное координатное уравнение кривой: r =#(0), как обычно, можно перейти к параметрическому представлению декартовой координаты, используя параметр B для параметра. Затем используйте (5), чтобы получить.

Смотрите также:

Решение задач по математическому анализу

Касательная плоскость к поверхности.	Круг кривизны и радиус кривизны.
Направление вогнутости, точки перегиба.	XVII век и анализ бесконечно малых.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.