Оглавление:


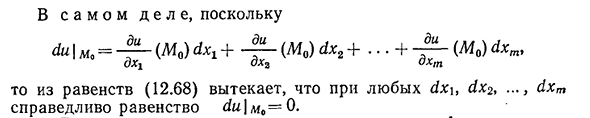

Понятие экстремума функции m переменных. Необходимые условия экстремума
- Понятие экстремума функции переменной M. Экстремальные требования. Функция t переменной u=f (M)=f(xi, x2,…, HT), точка L10 (H1°, H2°,…ET, пространство). О П Р Е Д Е Л Е Н и Е1. Например, если u=f(M)имеет 8 соседей точки L10, и значение f(M0)в ней является
наибольшим[наименьшим]из всех значений f(M)в этой функции, u=f (M)является наименьшим значением точки L10. О П Р Е Д Е Л Е Н и Е2. Предположим, что функция u=f(M) ‘ имеет точку
Mo l o K a l l l n Y y EXT R em mind, если она имеет либо локальный максимум, либо Людмила Фирмаль
локальный минимум в этой точке. Установлены необходимые условия для локальных экстремумов функции I=D7I). Докажите следующее: если функция u=f (M)=f (x\, x2,•••, Af0 (xi°, x2°,—>XT0) имеет частную производную первого порядка по всем переменным xi, x2,…., HT и это в§6. Локальные экстремумы 505 Если точка является
локальным экстремумом, то все первичные частные производные исчезают в точке Mo, т. е. axr(Mo)=0, dx (Mo)=0… , (МО)=0. (12.68) т. ахм Д О К А З а т е л ь с т в о. Попробуйте установить первым равного правосудия(12.68). Функция u = f (xi,XG…….HT) аргументы H2, H3,…, HT, поставить их равными соответствующему coor DIN=точка L1o, то есть
- положить x2=x2°, XS=X3°… , Xm=Xm°. Около Отсюда функция u=f (xi, x2°,… Производная этой функции от этой переменной в точке Xi=Xi°совпадает с производной в частных производных — — — — (Mo). Поскольку функция t переменной u=f (M) имеет локальный экстремум в точке a10, то указанная функция одной переменной zz=/: (xi, x2°,■■■, XT°) имеет локальный экстремум в точке Xi=Xi°, и первое равенство DHG (12.68) доказано. Остальные равенства (12.68) также были
доказаны. Подчеркнем, что равенства(12.68).E в заданной точке a (все частные производные первого порядка).исчезновение является только необходимым, но не достаточным условием для локальных экстремумов функции u=f (M) в точке Mo. Например, функция двух переменных I=XY имеет как частные производные, так и аннигилированные в Afo (O, 0), но DX не имеет экстремумов.A1o(O, 0)в этой точке Точки, в которых исчезают все первичные частные производные функции u=f (M),
называются в этой функции точками t A C и o n A R n s m и t. В каждой стационарной точке функции u=f (M) Людмила Фирмаль
возможны локальные экстремумы, но наличие этого экстремума может быть установлено только при достаточных условиях локального экстремума, уточнение которых осуществляется следующим образом: Если функция I==f (M)дифференцируема в точке a10 и имеет минимум в этой точке,то производные y и^11 этой функции в точке 7I0 одинаковы по отношению к производной независимой переменной dx\, dx2,.., ДХМ.506 ч. 12. Функции некоторых переменных Так как Du\M= — ^ — (Mo) dX1+(Mo) dx2+… +(Mo) dxm, DHG-DH2-auto тогда из уравнения (12.68), это dx\, dx2,…, dxm справедливое равенство^и] МО = О.
Смотрите также:
| Примеры вычисления площадей. | Производная по направлению. Градиент |
| Случай функции двух переменных | Непрерывность функции m переменных по одной переменной |

