Помощь по экономико математическим методам (ЭММ) — решение заданий и задач онлайн

Здравствуйте! Я Людмила Анатольевна Фирмаль, занимаюсь помощью студентам более 17 лет. У меня своя команда грамотных, сильных преподавателей. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И неважно – она по объёму на две формулы или огромная, сложно структурированная, на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.

Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Как получить помощь в выполнении заданий по экономико математическим методам (ЭММ)

Вы можете написать сообщение в WhatsApp. После этого я оценю ваш заказ и укажу стоимость и срок выполнения вашей работы. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за вашу работу, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл готовой работы в личные сообщения.

Сколько стоит помощь

Стоимость помощи зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости, загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.

Какой срок выполнения

Минимальный срок выполнения составляет 2-4 дня, но помните, срочные задания оцениваются дороже.

Как оплатить

Сначала пришлите задание, я оценю, после вышлю вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.

Гарантии и исправление ошибок

В течение 1 года с момента получения Вами готового решения действует гарантия. В течении 1 года я и моя команда исправим любые ошибки.

Чуть ниже я предоставила примеры оформления заказов по некоторым темам предмета экономико математические методы, так я буду оформлять ваши работы если закажите у меня, это не все темы, это лишь маленькая часть их, чтобы вы понимали насколько подробно я оформляю.

Возможно эта страница вам будет полезна:

Предмет экономико-математические методы (ЭММ)

Пример оформления заказа №1.

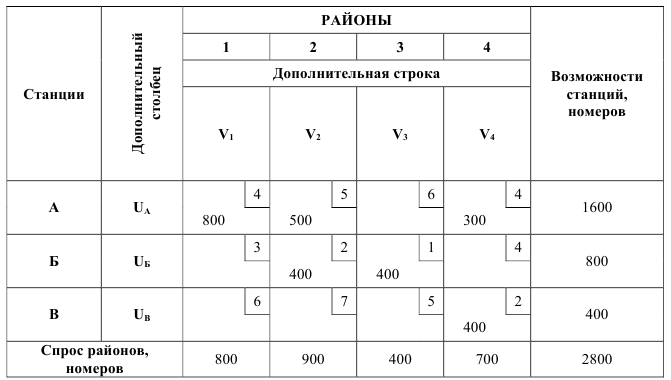
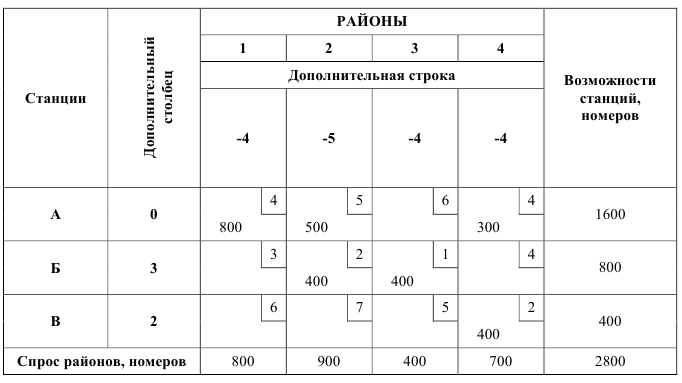
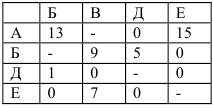
На территории города имеется три телефонных станции: А, Б и В. Незадействованные емкости станций составляют:

на станции А — 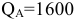номеров,

на станции Б — 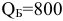номеров,

на станции В — 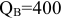номеров.

Потребности новых районов застройки города в телефонах составляют:

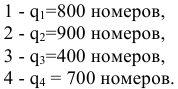
Необходимо составить экономико-математическую модель задачи и с помощью распределительного или модифицированного метода линейного программирования найти вариант распределения емкостей телефонных станций между районами новой застройки, который обеспечивал бы минимальные затраты как на строительство, так и на эксплуатацию линейных сооружений телефонной сети. Естественно, что таким вариантом при прочих равных условиях будет такое распределение емкости, при котором общая протяженность абонентских линий будет минимальной.

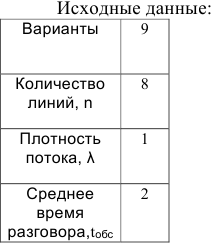
Исходные данные:

Решение:

Решение начнем с проверки соотношения между суммарной незадействованной емкостью телефонных станций и суммарным спросом на установку телефонов.

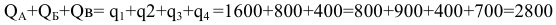
Задачи, в которых соблюдается равенство суммарной возможности пунктов отправления суммарному спросу пунктов назначения, называются транспортными задачами закрытого типа.

Задача заключается в нахождении такого распределения емкости, при котором общая протяженность абонентских линий была бы минимальной, т.е

Для решения задачи используем способ «наименьшего элемента», т.к этот метод позволяет получить решение более близкое к оптимальному.

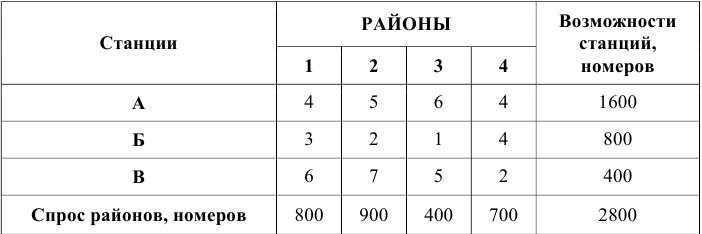
Из всех расстояний от станции до районов застройки выбираем наименьшую. Такой минимальной ценой в нашем примере является элемент БЗ, равный 1. С клетки БЗ следует начинать составление опорного плана. Спрос района 3 составляет 400 номеров, а станция Б может обеспечить 800 номеров. Следовательно, спрос района 3 может быть полностью удовлетворен за счет станции Б.

При этом остаток свободных номеров станции Б составляет 400 ед.

Вследствие того, что спрос района 3 удовлетворен полностью, столбец 3 в исходной таблице можно вычеркнуть. Наименьшими элементами, в оставшейся части таблицы являются Б2 и В4, выберем В4 наименьший элемент равен 2. Спрос района 4 полностью удовлетворяется станцией В. Вследствие того, что свободная номерная емкость станции В полностью использована, строку В исходной таблицы можно вычеркнуть. Так как элементов равных 2 было два следующей заполняем клетку Б2, спрос 2 района будет удовлетворен не полностью, так как на станции Б осталось всего 400 свободных номеров, которые мы и проставляем в данную клетку, после чего строку Б можно вычеркнуть. У нас осталась незаполненными клетки Al, А2 и А4 которые можно заполнить единственным образом, за счет станции А в соответствии со спросом.

Полученное методом наименьшего элемента решение задачи показано в таблице 3 протяженность линий согласно этому решению составит:

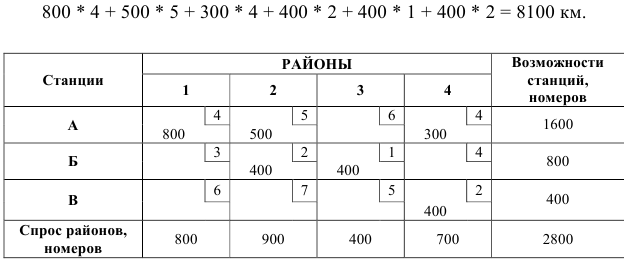
Составим таблицу модифицированного распределительного метода, принимая в качестве исходного решение по методу наименьшего элемента.

Основное отличие модифицированного распределительного метода заключается в порядке исследования свободных мест таблицы с помощью дополнительных строки и столбца.

Первый этап расчетов заключается в определении значений клеток, образующих дополнительную строку и дополнительный столбец. Во всех случаях верхняя клетка дополнительного столбца (строка А) получает значение 0. Этот 0 будет фигурировать в процессе всего решения.

Рассчитаем значения других дополнительных клеток. Если значения клеток, образующих дополнительный столбец, обозначить через 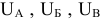, а значение клеток, образующих дополнительную строку — 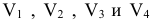, то исходным положением для расчета их значений будет равенство 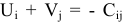, где 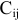-среднее расстояние от станции до районов застройки и клетка на пересечении рассматриваемых строки и столбца. При этом определяются значения клеток тех столбцов и строк, пересечения которых образуют занятые места.

Начнем с первой клетки дополнительного столбца, значение которой принято равным 0. Для столбца, соответствующего району 1, имеем 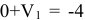; отсюда .

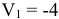Для столбца 2: .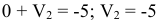

Для столбца 4: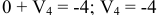

Для столбца 3 в строке А такого равенства составить нельзя, так как клетки A3 является свободным местом.

Аналогично составим уравнения для строки Б: 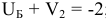; так как 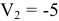, получим:

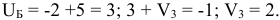
Для строки В:

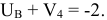
Но поскольку 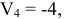то .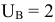

Получены значения всех клеток, образующих дополнительные строку и столбец. Эти значения записываются на соответствующие места в таблице:

Найденные значения клеток позволяют провести исследование свободных мест. Его целью является выявление отрицательных свободных мест. Если 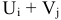меньше соответствующего значения расстояния (в клетке на пересечении 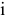-й строки и 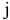-го столбца), взятого с обратным знаком, то свободное место 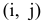отрицательно и решение может быть улучшено.

Для свободных мест:

Неравенства показывают, что характеристики всех свободных мест положительные, значит план оптимальный.

Пример оформления заказа №2.

Необходимо оценить работу автоматической телефонной станции (АТС), которая имеет 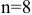линий связи. Моменты поступления вызовов на станцию являются случайными и независимыми друг от друга. Средняя плотность потока равна 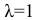вызову в единицу времени. Продолжительность каждого разговора является величиной случайной и подчинена показательному закону распределения. Среднее время одного разговора равно 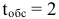единицы времени.

Автоматические телефонные станции относятся к типу систем обслуживания с потерями (с отказами). Абонент получает отказ в случае, если все линии заняты.

Для определения основных показателей работы АТС необходимо рассчитать значение поступающей нагрузки в Эрлангах 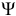и вероятности, что из 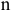-линий 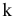будет занято

Для расчета используются формулы:

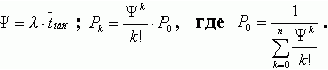
Далее следует определить вероятность отказа 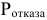, среднее число занятых и среднее число свободных линий, коэффициенты занятости и простоя линий и сделать вывод о качестве обслуживания абонентов и эффективности использования линий связи.

Решение:

• Определим значение поступающей нагрузки 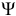по формуле

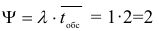
• Найдем вероятность того, что все линии связи свободны по формуле:

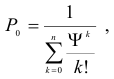
где 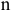количество линий связи,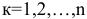

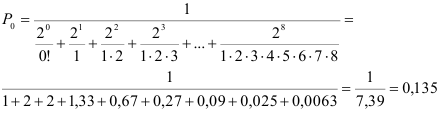
Вероятность того, что все линии связи будут свободны, составляет 13,5%

• Рассчитаем вероятности занятости 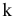-линий из 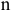, по формуле

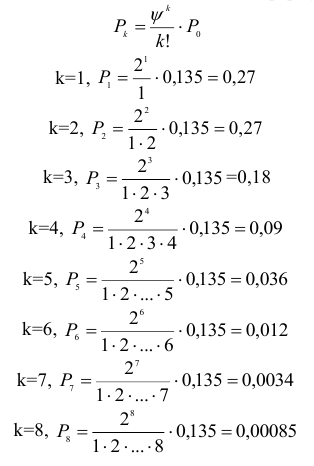
• Найдем вероятность того, что все линии связи заняты, т.е. вероятность отказа, по формуле:

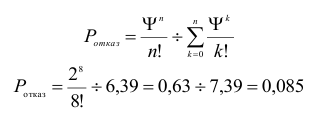
Вероятность отказа равна 8,5%.

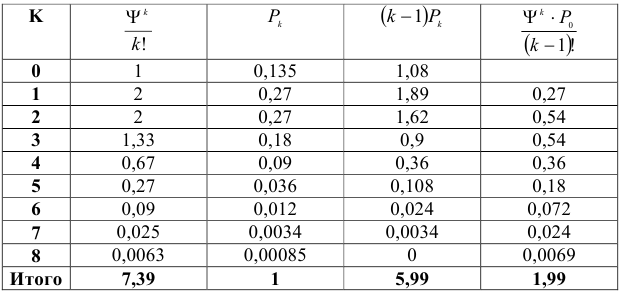
• Найдем среднее число занятых линий по формуле:

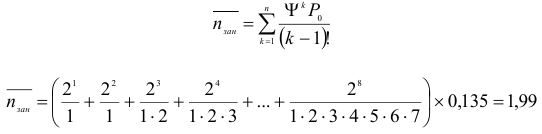
Среднее число занятых линий равняется 1,99.

• Коэффициент занятости линий

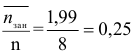
• Найдем среднее число свободных линий по формуле:

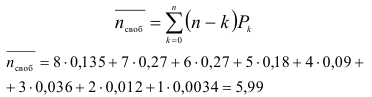
Среднее число свободных линий равно 5,99

Коэффициент простоя линий

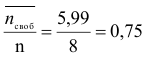
Коэффициент простоя можно было посчитать другим методом 1-0,25=0,75

Вывод: качество обслуживания абонентов приемлимое, потому как вероятность отказа составляет 8,5%, но эффективность использования линий низкая, потому что очень высокий процент простоя линий связи 75%.

Пример оформления заказа №3.

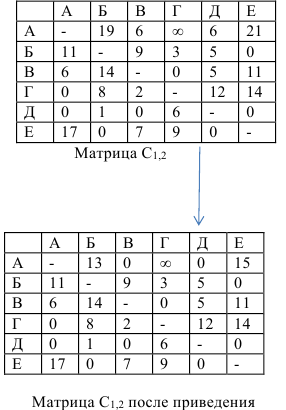
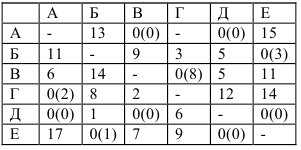
В таблице приведены затраты времени почтальона (в минутах) на проход между пунктами доставки на участке. Используя метод «ветвей и границ», найти маршрут почтальона, при котором затраты времени на его проход будут минимальными.

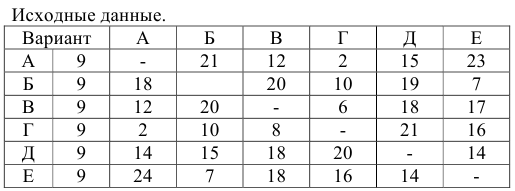
Решение:

Задачу решаем методом теории графов, известным как метод «ветвей и границ».

Матрица считается приведенной, если в каждой строке и каждом столбце содержит не менее одного нуля. Для приведения исходной матрицы сначала в каждой строке находится наименьший элемент и вычитается из элементов своей строки, затем в приведенной по строкам матрице в каждом столбце находится наименьший элемент и вычитается из элементов своего столбца — получается приведенная матрица.

Обозначим за Г множество всех обходов почтальона (т. е. всех простых ориентированных остовных циклов). Поскольку граф — полный, это множество заведомо не пусто. Сопоставим ему число 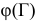, которое будет играть роль значения на этом множестве оценочной функции: это число равно сумме констант приведения данной матрицы весов дуг графа и является оценкой снизу для стоимости минимального тура коммивояжёра. Приведённую матрицу весов данного графа следует запомнить, обозначим ее через .

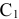Подсчитаем 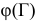. Для этого выполним приведение матрицы весов. Сначала — по строкам:

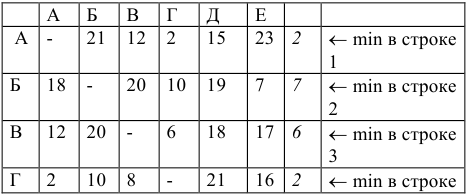
Сумма констант приведения

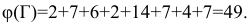
Обозначим полученную матрицу через 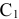и найдём в ней самый тяжёлый нуль. Заметим, что замена нулевого элемента на 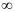приводит к изменению лишь двух слагаемых суммы констант приведения 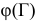— по одному при приведении строк и столбцов. Поэтому вес нуля можно определить суммированием наименьших элементов его строки и столбца.

Например, вес нуля в первой строке и четвёртом столбце складывается из минимума по первой строке, равного 6 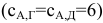, и минимума по четвёртому столбцу Г, равного 0 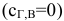, без учета самого .

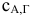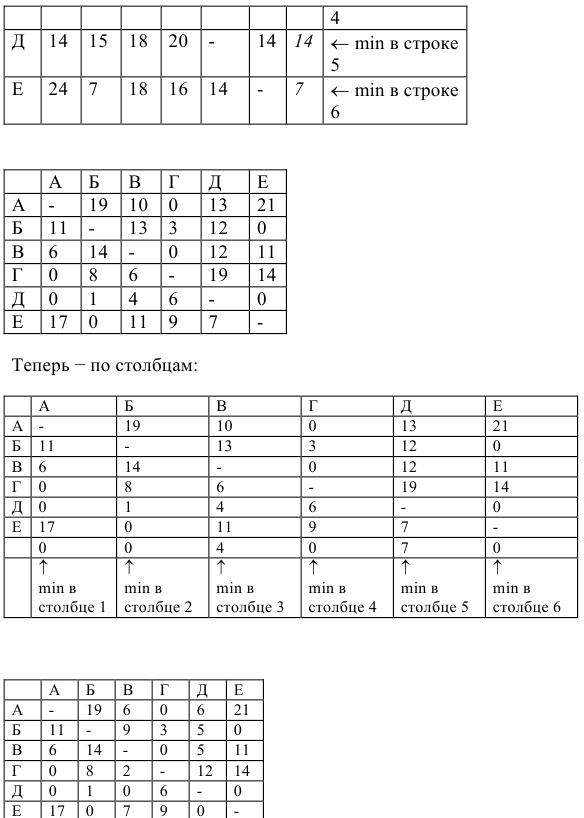
Итак, запишем приведённую матрицу еще раз, указывая рядом с каждым нулем его вес:

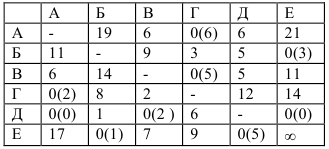
Самым тяжелым оказывается нуль в клетке (А,Г).

Разобьём множество Г на две части: множество 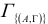(все циклы, проходящие через дугу (А,Г)) и (все циклы, не проходящие через дугу (А,Г)). Такое ветвление определяет необходимость выбора одного из этих вариантов. Множеству соответствует матрица 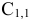, полученная вычёркиванием соответствующих строки (строку А) и столбца (столбец Г).

У оставшихся строк и столбцов сохраним их исходные номера.

Разумеется, вместе с вычёркиванием строки и столбца, в матрице надо заменить на 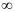; числа в определённых клетках так, чтобы не получалось коротких циклов (длиной меньше 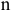). В данном случае из города Г мы уже не можем проехать в город А, поэтому в клетке (А,Г) ставим знак .

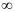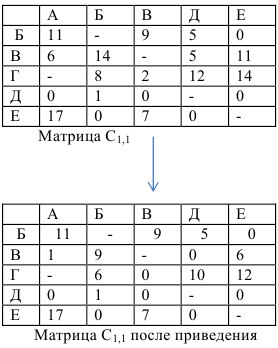
Сумма констант приведения матрицы 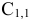здесь равна 7, поэтому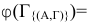 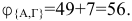. Сопоставим результат 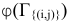множеству 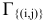, (в нашем случае ).

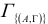Множеству 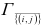(в нашем случае 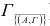) в свою очередь, соответствует другая матрица — 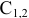полученная заменой на 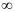элемент 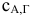в матрице :

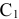Сумма констант последнего приведения равна 6, так что

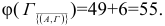
Теперь выберем между множествам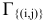и и 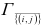то, на котором минимальна функция 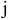. В нашем случае из множеств, которому соответствует меньшее из чисел

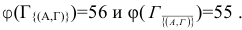
Поэтому дальнейшей разработке подвергнется множество 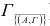. Итак, выделена определенная дуга (А,Г) графа и построены новые матрицы, к которым, очевидно, можно применить описанную выше процедуру. При каждом таком повторном применении будет фиксироваться очередная дуга графа, которая в конечном итоге войдёт в искомый гамильтонов цикл , если данная ветвь будет продолжена до конца и иметь минимальный вес.

В матрице 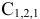подсчитаем веса нулей (веса нулей указаны в скобках):

Самым тяжёлым является нуль с номером (В,Г), так что теперь следует рассматривать множества 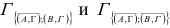. Обратимся к первому из них.

Необходимо заменить на 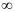числа во всех тех клетках, которые соответствуют ребрам, заведомо не принадлежащим тем циклам, которые проходят через уже отобранные ранее ребра.

Поскольку, вычеркнув строку В и столбец Г в матрице 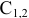, нужно также заменить на 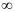числа в определённых клетках так, чтобы не получалось коротких циклов (длиной меньше 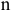), то в клетке с номером (В,Г) надо поставить символ 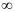. Получим матрицу :

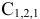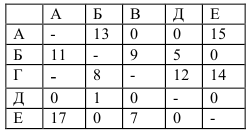
Сумма констант остается неизменной, так как матрица не требовала приведения

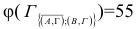
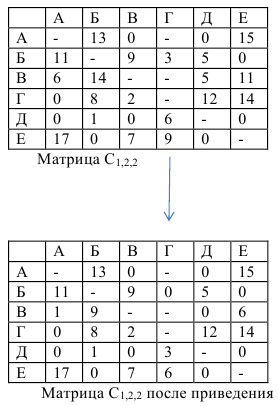
Сумма констант приведения

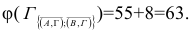
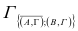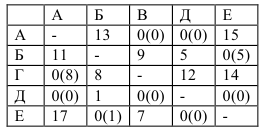
Следовательно дальнейшей разработке подлежит «Взвешиваем» нули в матрице :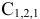

Самым тяжелым является нуль с номером (Г,А), теперь рассмотрим множества

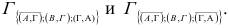
Вычеркиваем строку Г и столбец А , ставим в клетке (А,Г) и получаем матрицу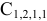

Матрица не требует приведения и сумма констант приведения останется без изменений

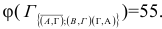
Рассмотрим матрицу :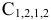

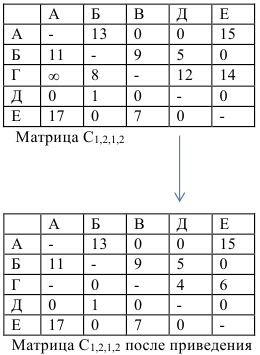
Сумма констант приведения

Произведем оценку нулей в матрице :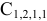

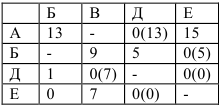
Самый тяжелый вес равный 13 имеет нуль в клетке с номером (А,Д), следовательно будем рассматривать множества

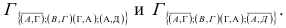
Вычеркиваем строку А и столбец Д и заменяем число в клетке (Д,В) на знак .

Получаем матрицу :

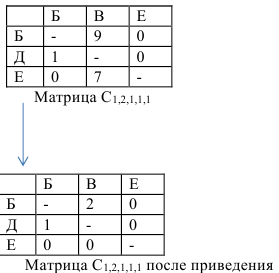
Сумма констант приведения

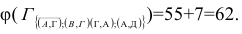
Для множества

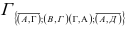
а 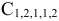приобретает вид:

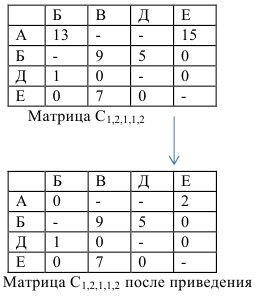
Сумма констант приведения

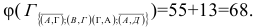
Следовательно дальше разрабатываем матрицу

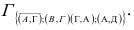
«Взвешиваем» нули в матрице :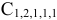

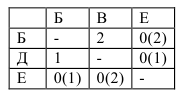
У нас получилось два одинаково тяжелых нуля, разработаем матрицы

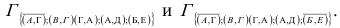
Вычеркиваем строку Б и столбец Е и заменяем число в клетке (Б,Е) на 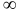. Получаем матрицу :

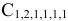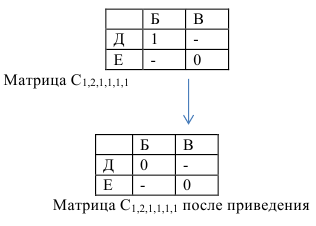
Сумма констант приведения

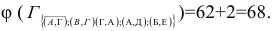
Рассмотрим матрицу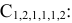

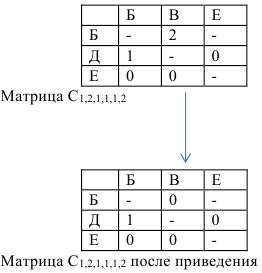
Сумма констант приведения

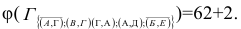
Получается что для дальнейшей разработки можно брать любое из множеств, если мы возьмем матрицу 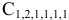то можно отработать матрицу

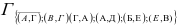
и следовательно мы получим кольцевой маршрут следующего вида:

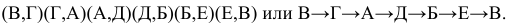
Пример оформления заказа №4.

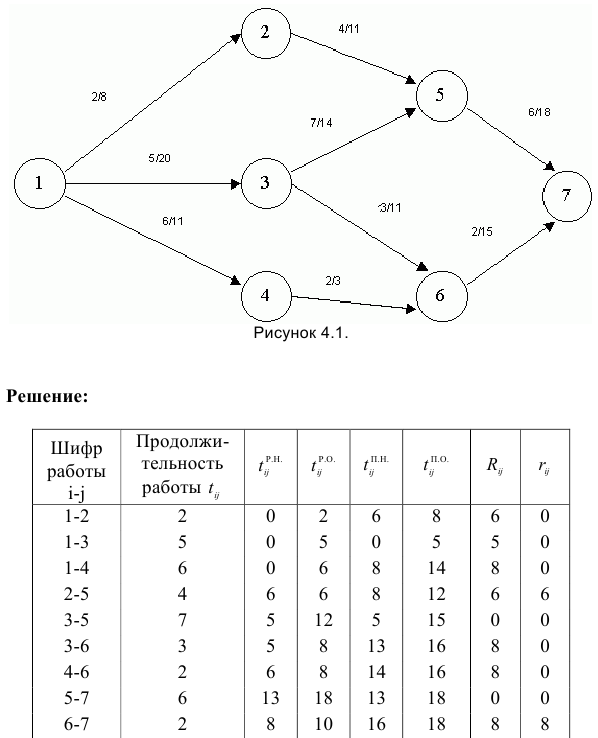
На сетевом графике (рис.4.1) цифры у стрелок показывают в числителе -продолжительность работы в днях, в знаменателе — количество ежедневно занятых работников на её выполнение.

В распоряжении организации, выполняющей этот комплекс работ. Имеется 28 рабочих, которых необходимо обеспечить непрерывной и равномерной работой.

Используя имеющиеся запасы времени по некритическим работам, скорректируйте сетевой график с учётом ограничения по количеству рабочих.

Возможно эти страницы вам будут полезны:

• Экономико-математические методы задачи с решением и примерами
• Решение задач по ЭММ
• Решение экономико математических методов
• Курсовая работа по экономико математическим методам
• Контрольная по экономико математическим методам
• Заказать работу по экономико математическим методам