Полное приращение и дифференциал
Полным приращением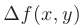 
называют такое приращение функции 
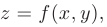которое обусловлено изменением значений всех независимых переменных. Таким образом, имеем
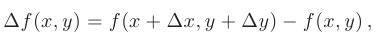
где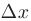 
и 
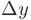— приращения соответствующих независимых переменных.
Под дифференциалом независимой переменной понимается приращение этой переменной:
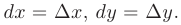
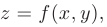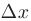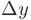Полным дифференциалом (или просто дифференциалом) функции двух независимых переменных называется главная часть ее полного приращения, линейная относительно и . Дифференциал функции можно представить в виде:
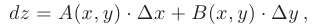
где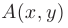 
и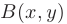 
не зависят от 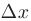и 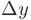и, сверх того
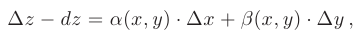
где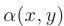 
и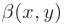 
— бесконечно малые при 
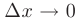и 
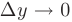. Дифференцируемой в данной области называется функция 
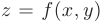, имеющая в этой области дифференциал 
.
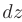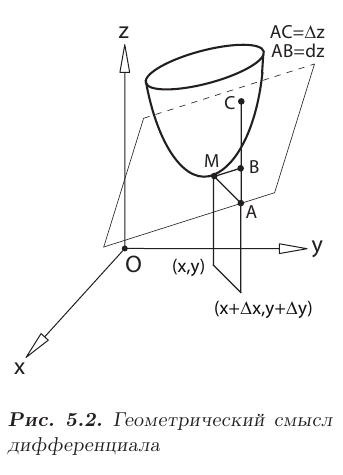
Геометрически дифференциал 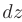функции двух переменных есть приращение аппликаты касательной плоскости к поверхности 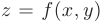в данной точке, когда переменные 
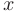и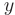 
получают приращение 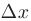и 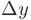(см. рис. 5.2).
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Функция многих переменных в математике |
| Непрерывность и частные производные в математике |
| Достаточное условие дифференцируемости в математике |
| Производная по направлению и градиент в математике |
