Почленный переход к пределу

Оглавление:

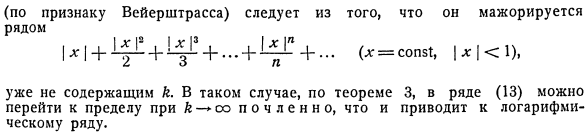
Почленный переход к пределу

Почленный переход к пределу. Другая теорема 1 является обобщением теоремы 1.& В нем является произвольным бесконечным множеством с точкой конденсации a (конечным или нет) [n°32].Сама эта точка может не принадлежать множеству 5C. Теорема 3.Каждая функция un (x) (η= 1, 2, 3,…) Определяется в области 5C, и из-за тренда от x до a существует конечный предел. Итн ЦН (х)= СП. (8） X * С 2 СП = с(с） н»я И 2) Серия(1) total f (x) также имеет x * a-подобные ограничения. Тю /(х) = С.(9 )） Х * * 00 Доказательство. Согласно требованию равномерного спуска для любого Эпсилона > 0 η°26b, ETA>> /и / k = 1, 2, 3,…Есть неравенство. p. 74 радует, что все x идут здесь до предела x.* a, принимая во внимание(8）、 Я CN + \ + Ки+ 2 +•••сп + т я е «.

Если ряды в области сходятся равномерно, то сходятся ряды, составленные из этих пределов. Людмила Фирмаль

Поэтому для ряда © выполняется условие сходимости n°242. C, Cn и среднее, как обычно, для его количества, частичного количества и баланса、 с = КТ + Т Вычитание этого члена равенства в терминах из (2) облегчает его получение. \ /(х)-с \ / п (х)-CN я + я?(x) I + 1 т |. (10 )） Учитывая равномерную сходимость ряда (1) и сходимость ряда ©, если ε]]> 0, то мы можем очень сильно зафиксировать η для всех x при 5C следующим образом: 1?»МКР и | тп / д -.«О1） Очевидно. Тогда-если вы хотите ограничиться случаем конечного a-есть 8 O, а x-a / 8: (12） | / «С*) Ж / 4. Тогда для величины указанного Пи (10), (11) и по (12) неравенство 1 / ( * ) C / e (9)) привести к. Да. И МПС 2 „л(•)= 2 {1“ Ж ООН(.*）}; х * АП = ін = 1 х Уравнение (9) может быть записано в следующем формате[см. (8）].

То есть в функциональном ряду предельный переход равен * за период. Примеры в качестве приложения этой общей теоремы мы используем предельные соотношения W * 25b, (21)|(26) / (26)} на основании выводов журнала серии известны читателю） ЛН = тю к(м / а 1). Йоу. (В сущности, именно так Эйлер достигает логарифмического ряда при введении анализа, но, конечно, строгого обоснования этому нет!） положите a = 1 + (где | lr | 1) и его расширение вместо (I- x) ±(±_Л (1 + ДГ）* = 1 + 1 * ±*-> * ^ + Митч!),.+ … Тогда ln (1+) появляется как предел (13 )） т (’т) (’т) у ^ ТП)+’» Здесь мы подчеркиваем, что x означает константу.

Итак, если существует равномерная сходимость, то предел суммы функционального ряда равен сумме ряда, состоящего из пределов его членов. Людмила Фирмаль

Члены этого яда содержат естественный параметр K в качестве переменной. Для всей области его изменения 1)*) ряд (13) сходится uniformly. It есть *) В этой дискуссии читатель поймет, что теорема 1 уже была применена для ее доказательства. ** ) Напомним, что переменная x переменной области 5C, описанная в теореме 3, может быть anything. In в частности, из-за того, что o = + oo можно свести к набору натуральных чисел. От того, что он специализировался рядом (на базе All-Strasse) М4-ТС ^ 4-ЦР + … + ЦР+ …(*=const1,| * / 1）、 Он уже содержит k. In в этом случае, по теореме 13 серии 3, предел может быть достигнут как член© * °°и стать логарифмом.

Непрерывность суммы ряда.	Почленное интегрирование рядов.
Функциональные свойства суммы ряда. Случай положительных рядов.	Почленное дифференцирование рядов.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.