Плотностью распределения вероятностей непрерывной, случайной величины 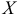 называют функцию
называют функцию 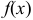 — первую производную от функции распределения
— первую производную от функции распределения 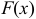 :
:
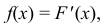
т.е. функция распределения является первообразной для плотности распределения.
Для дискретной, случайной величины плотность распределения неприменима.
Теорема. Вероятность того, что непрерывная случайная величина 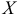 примет значение, принадлежащее интервалу
примет значение, принадлежащее интервалу 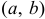 равна:
равна:
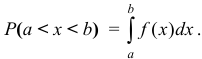
Если 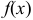 — чётная функция, то
— чётная функция, то 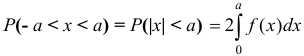 .
.
Зная плотность распределения 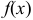 , можно найти функцию распределения:
, можно найти функцию распределения:
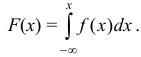
Свойства плотности распределения
1) Плотность распределения неотрицательная функция: 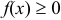 .
.
2) Несобственный интеграл от плотности распределения в пределах от 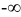 до
до 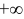 равен единице:
равен единице: 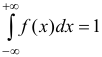 .
.
3) Если все возможные значения случайной величины принадлежат интервалу 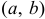 , то
, то 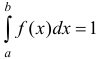 .
.
Функция 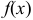 определяет плотность распределения вероятности для каждой точки
определяет плотность распределения вероятности для каждой точки 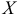 аналогично плотности массы в точки.
аналогично плотности массы в точки.
На этой странице размещён краткий курс лекций по теории вероятностей и математической статистике с теорией, формулами и примерами решения задач:
Теория вероятностей краткий курс для школьников и студентов
Возможно вам будут полезны эти страницы:

