Оглавление:
Плоскопараллельное движение твердого тела
Называют такое движение твердого тела, при котором скорости всех его точек параллельны некоторой неподвижной плоскости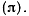 
Сечение твердого тела плоскостью 
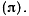(или плоскостью, ей параллельной) представляет собой плоскую фигуру, неизменно связанную с твердым телом. Как мы уже видели, три точки твердого тела, не лежащие на одной прямой, однозначно определяют положение твердого тела. Поэтому движение плоского сечения должно полностью определять и движение самого твердого тела.
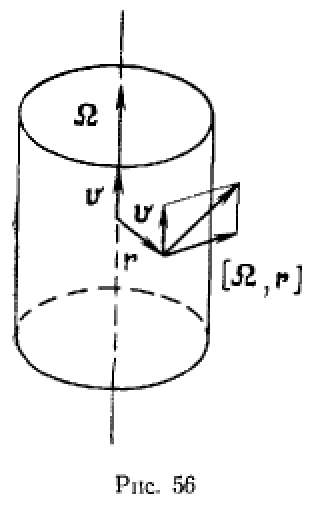
В общем случае мгновенно-винтового движения твердого тела скорости точек твердого тела складываются из скорости движения вдоль винтовой оси и скорости от вращения вокруг мгновенной винтовой оси. При этом скорости точек твердого тела не расположены в одной плоскости. Они лежат в касательных плоскостях к поверхности прямого кругового цилиндра, ось которого совпадает с мгновенной винтовой осью (рис. 56). Скорости всех точек твердого тела будут параллельны одной плоскости лишь в тех случаях, когда мгновенное движение либо поступательное, либо вращательное. В первом случае мгновенная винтовая ось параллельна плоскости 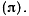во втором — ортогональна к плоскости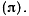
Заметим, что мгновенно-поступательное движение можно рассматривать как предельный случай мгновенно-вращательного движения. В самом деле, произвольное мгновенно-вращательное движение твердого тела с угловой скоростью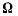 
всегда можно пред-
представить как сложение двух мгновенных вращений вокруг
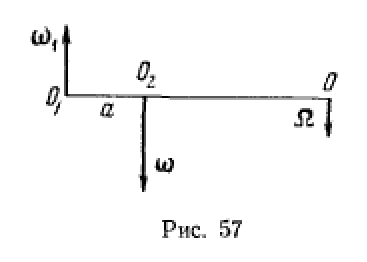
параллельных осей со скоростями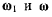 
(рис. 57), удовлетворяющими условиям
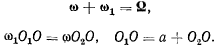
Мгновенно-поступательному движению будет соответствовать
предельный случай двух вращений, когда величина угловой скорости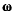 
неограниченно приближается к величине угловой скорости 
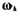Расстояние до мгновенной оси вращения
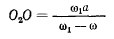
в этом случае стремится к бесконечности, а величина мгновенной
угловой скорости 
стремится к нулю. Таким образом, мгновенно- поступательное движение представляет собой предельный случай мгновенного вращения, когда величина мгновенной угловой скорости стремится к нулю, а мгновенная ось вращения уходит в бесконечность.
Мгновенное плоскопараллельное движение твердого тела всегда можно привести к одному мгновенному вращению, мгновенная ось вращения которого ортогональна к плоскости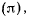 
параллельной скоростям точек твердого тела. При непрерывном движении твердого тела направления скоростей его точек все время остаются параллельными одной и той же неподвижной плоскости 
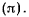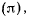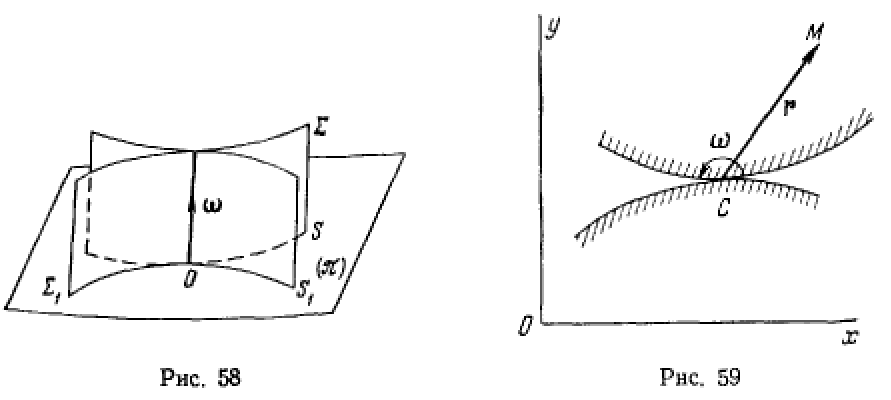
В каждый момент движение представляет собой вращение мгновенной оси, ортогональной к плоскости а аксоиды в плоскопараллельном движении представляют собой цилиндрические поверхности, образующие которых ортогональны к плоскости 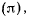(рис. 58). Аксоиды пересекаются с плоскостью 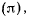по двум кривым, называемым центроидами (полодиями), а точка пересечения мгновенной оси вращения с плоскостью 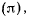называется мгновенным центром вращения. Непрерывное движение твердого тела в плоскопараллельном движении можно представить как качение без скольжения подвижной центроиды по неподвижной. В самом деле, если выбрать неподвижную систему осей так, чтобы плоскость 
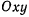совпадала бы с плоскостью 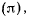а ось z была бы ортогональна к плоскости 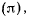то, обозначив координаты мгновенного центра вращения через 
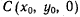и координаты произвольной точки М твердого тела через 
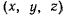(рис. 59), из формулы Эйлера
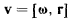
определим проекции скорости точки М. При помощи матрицы
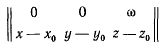
находим
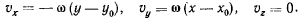
Из этих формул видно, что скорость точки не зависит от
координаты z и все точки твердого тела, лежащие на прямой,
ортогональной к плоскости 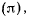имеют одни и те же скорости. Следовательно, мгновенное движение твердого тела полностью определяется
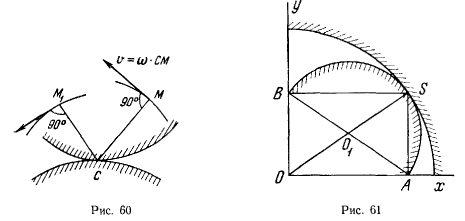
движением точек плоской фигуры, т. е. качением без скольжения подвижной центроиды по неподвижной. Точка твердого тела, совпадающая в данный момент с мгновенным центром вращения, имеет скорость, равную нулю. Если положение мгновенного центра вращения известно, то скорость произвольной точки твердого тела, лежащей в плоскости 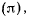ортогональна к прямой, соединяющей эту точку с мгновенным центром вращения (рис. 60). Вектор скорости точки М направлен по касательной к ее траектории, которую называют рулеттой точки. Зная рулетты двух точек 
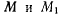твердого тела, можно определить геометрическое место мгновенных центров вращения твердого тела (центроиды), которые лежат на пересечении нормалей к рулеттам (если только эти нормали не совпадают).
Пример:
Палочка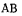 
скользит концами по сторонам прямого угла
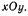Найти центроиды (рис. 61).
Решение:
Точка А скользит по оси х, а точка В — по оси у. Эти осн являются рулеттами точек А и В. Мгновенный центр вращения S лежит на пересечении перпендикуляров к осям х и у. Фигура OBSA — прямоугольник. Отсюда следует, что расстояние точки S от неподвижной точки О остается постоянным и равно длине палочки, т. е. геометрическое место мгновенных центров вращения в неподвижном пространстве есть окружность. Диагонали в прямоугольнике делятся пополам, поэтому расстояние точки S от середины палочки тоже равно половине длины последней, а геометрическое место мгновенных центров вращения относительно палочки (подвижная центроида) есть окружность с центром в середине палочки и радиусом, равным половине ее длины.
Пример:
Палочка АВ длиной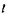 
движется в неподвижной плоскости так, что всегда проходит через точку М неподвижной окружности радиуса 
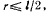конец палочки скользит по внутренней стороне этой окружности. Найти траектории точек палочки, а также центроиды ее движения (рис. 62).
Решение:
Обозначим через а расстояние точки С от конца палочки А, тогда расстояние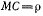 
будет
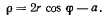
Такая кривая называется улиткой Паскаля. Чтобы определить положение мгновенного центра вращения, найдем рулетты
Рис. 62 двух точек палочки А и М. Рулетга точки А — окружность, и, следовательно, мгновенный центр вращения лежит на прямой
АО, проходящей через центр окружности. Рулетта точки М — улитка Паскаля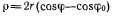 
Касательная к рулетте в точке М направлена вдоль скорости точки М палочки. Направление же скорости точки М найдем, рассматривая движение неподвижной точки М (острия) в системе координат, связанной с палочкой. Абсолютная скорость точки М острия равна нулю. В системе, связанной с палочкой, точка М острия скользит по палочке, и, следовательно, — относительная скорость направлена вдоль палочки. Переносная скорость точки М острия— это скорость точки М палочки. Из теоремы о сложении скоростей имеем
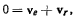
откуда следует, что переносная скорость тоже направлена вдоль палочки. Итак, мгновенный центр вращения палочки расположен на прямой, ортогональной к палочке и проходящей через точку М. Мгновенный центр вращения S находится в точке пересечения прямых АО и MS. Прямой угол AMS всегда опирается на диаметр окружности, на которой лежат точки А и S. Поэтому точка S также лежит на окружности с центром в точке О. Для определения центроид, заметим, что при изменении положения палочки точка S всегда остается на окружности, центр которой находится в точке О, а радиус равен r. Эта окружность и будет неподвижной центроидой. Расстояние точки S от точки А палочки не изменяется и всегда равно 2 r, поэтому подвижной центроидой будет окружность радиуса 2 r с центром в точке А.
Пример:
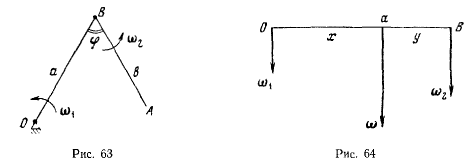
Стержень ОВ вращается в неподвижной плоскости вокруг
точки О с постоянной угловой скоростью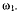 
Со стержнем ОВ шарнирно соединен второй стержень ВА, который также вращается в той же плоскости вокруг точки В, причем угол 
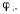между стержнями АВ и ОВ изменяется по закону 
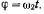Определить центроиды стержня ВА (рис. 63).
Решение:
Рулеттой точки В является окружность с центром в точке О, так что мгновенный центр вращения стержня ВА лежит на нормали к рулетте, т. е. на прямой ОВ. Стержень ВА участвует в двух вращениях вокруг параллельных осей, причем векторы угловых скоростей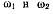 
направлены в одну и ту же сторону (рис. 64). В этом случае результирующее движение также мгновенное вращение, причем величина угловой скорости результирующего вращения
Вектор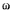 
направлен в ту же сторону, что и векторы 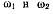а положение линии действия определяется из уравнений
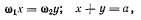
откуда
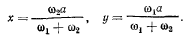
Расстояние мгновенного центра вращения от точки О
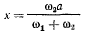
не изменяется, если остаются неизменными величины 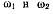В этом случае неподвижной центроидой является окружность радиуса х с центром в точке О. Расстояние мгновенного центра вращения от точки В палочки АВ равно
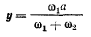
и также остается постоянным, если не изменяются 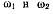Подвижной центроидой является окружность с центром в точке В и радиусом у. Непрерывное движение палочки АВ можно представить как качение без скольжения подвижной окружности по неподвижной.
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:
Предмет теоретическая механика
Эти страницы возможно вам будут полезны:
| Теорема Эйлера |
| Мгновенное движение твердого тела с одной неподвижной точкой |
| Ускорение точки в сложном движении |
| Замечание о дифференцировании единичного вектора |
