Плоские и пространственные кривые линии
Для построения ортогональных проекций кривой необходимо построить проекции ряда точек, принадлежащих этой кривой, и через них провести под лекала плавные кривые. Следует иметь в виду, что по двум проекциям нельзя без дополнительных построений определить, является линия пространственной или плоской кривой.
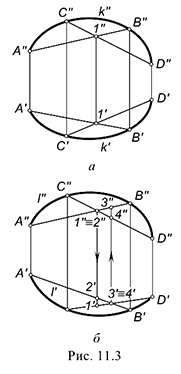
На рис. 11.3 показаны эти дополнительные построения, которые позволяют сказать: вверху приведен чертеж плоской кривой 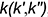 , а под ним -пространственной
, а под ним -пространственной 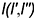 . Суть дополнительных построений сводится к соединению попарно четырех точек
. Суть дополнительных построений сводится к соединению попарно четырех точек 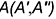 и
и 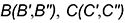 и
и 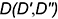 , произвольно взятых на кривой, прямыми линиями.
, произвольно взятых на кривой, прямыми линиями.
Поскольку на рис. 11.3, а эти прямые являются пересекающими, о чем свидетельствует расположение проекций 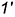 и
и 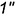 точки их пересечения на одной линии связи, то все указанные точки
точки их пересечения на одной линии связи, то все указанные точки 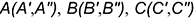 и
и 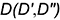 лежат в одной плоскости. В силу этого линия
лежат в одной плоскости. В силу этого линия 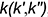 , которой принадлежат эти точки, является плоской кривой (у плоской кривой все принадлежащие ей точки должны лежать в одной плоскости).
, которой принадлежат эти точки, является плоской кривой (у плоской кривой все принадлежащие ей точки должны лежать в одной плоскости).
Внизу на рис. 11.3, б отмеченное условие не выполняется — точки пересечения проекций прямых, попарно соединяющих проекции четырех точек 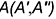 и
и 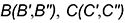 и
и 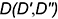 , принадлежащих кривой
, принадлежащих кривой 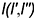 , лежат на разных линиях связи. Следовательно, эти прямые не лежат в одной плоскости, являясь скрещивающимися. Поэтому не лежат в ней и соединяемые ими точки кривой, свидетельствуя о том, что эта линия — пространственная кривая.
, лежат на разных линиях связи. Следовательно, эти прямые не лежат в одной плоскости, являясь скрещивающимися. Поэтому не лежат в ней и соединяемые ими точки кривой, свидетельствуя о том, что эта линия — пространственная кривая.
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Начертательная геометрия для 1 курса
Возможно эти страницы вам будут полезны:
| Примеры построения аксонометрических проекций |
| Кривые линии и поверхности |
| Кривые поверхности |
| Цилиндрические и конические винтовые линии |

