Задача №92. Пластинка 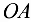, поворачиваясь относительно оси шарнира

Задача №92.

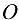Пластинка , поворачиваясь относительно оси шарнира , может устанавливаться под любым углом к горизонту (рис. 3.57, а). На пластинке лежит тело 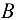весом . Определить наибольший угол 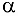наклона пластинки, при котором тело будет оставаться в равновесии.

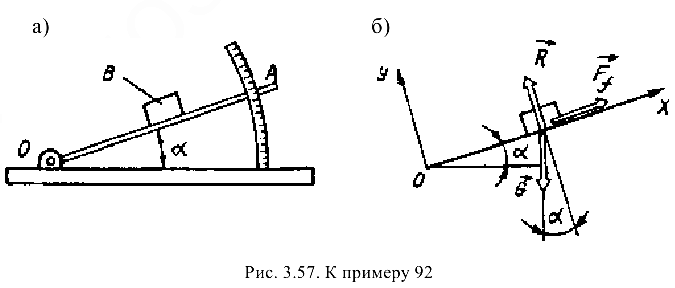
Решение:

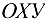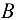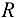Примем систему координат . На тело действуют сила тяжести , нормальная реакция и сила трения 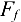(рис. 3.57, б).

Составим уравнения равновесия тела:

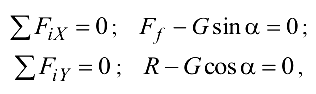
из которых найдём

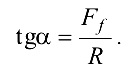
Заметим, что отношение силы трения 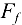к нормальной реакции 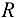есть коэффициент трения 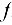. Тогда угол 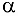будет углом трения 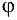: 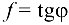. Таким образом, для равновесия тела необходимо, чтобы выполнялось условие .

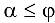С помощью рассматриваемого простого устройства можно экспериментально определять коэффициенты трения скольжения.

Например, в момент начала движения стального бруска по стальной пластине 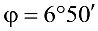; следовательно, коэффициент трения стали по стали .

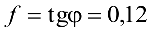Ответ: .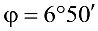

Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:

Решение задач по прикладной механике

Возможно эти страницы вам будут полезны:

Задача №90. Механизм манипулятора, состоящий из трёх звеньев, соединённых шарнирами, в положении равновесия расположен в вертикальной плоскости (рис. 3.54, а).

Задача №91. Пример имеет своим прототипом схему подъема мачтовых опор ЛЭП с помощью тягачей (рис. 3.55).

Задача №93. Груз весом = 280 Н подвешен в точке горизонтальной балки весом = 160 Н. Балка укреплена при помощи шарнира и свободно опирается концом на балку весом = 120 Н. Балка имеет шарнир и концом опирается на гладкую вертикальную стену.

Задача №94. Две балки и одинаковой длины = 3 м соединены между собой шарниром (рис. 3.60, а). Конец балки заделан в вертикальной стене, а конец балки опирается па подвижную опору, расположенную под углом = 30° к оси балки . На балку по всей её длине действует равномерно распределённая нагрузка интенсивностью = 3 кН/м. На балку действует сила = 10 кН, приложенная в середине балки под углом = 60° к её оси. Определить реакции опор и , а также в шарнире , пренебрегая силами тяжести балок.