Оглавление:
Первый замечательный предел
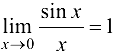
Доказательство.
Рассмотрим круг радиусом R с центром в точке О. Пусть ОА -неподвижный радиус, ОВ — подвижный, образующий угол 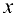
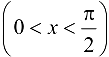 радиусом ОА (рис. 3.2).
радиусом ОА (рис. 3.2).
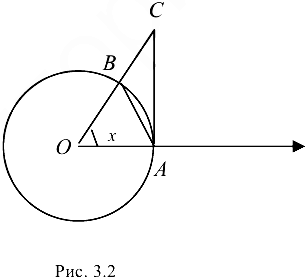
Проведем из точки А перпендикуляр к радиусу ОА до пересечения в точке С с продолжением радиуса ОВ. Тогда
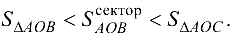
Так как 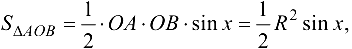
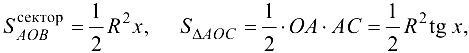
то неравенства (3.2) примут вид
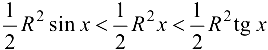
после умножения на 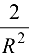 имеем
имеем 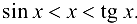
Разделим все члены неравенств на 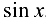 . Получим
. Получим
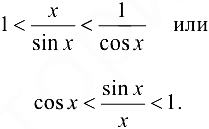
Вычтем (3.3) из числового тождества 1 = 1 = 1.
Получим
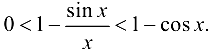
Так как 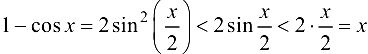 , то при
, то при 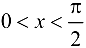
получаем
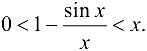
Возьмем 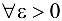 и положим
и положим 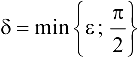 Тогда для всех
Тогда для всех 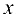 , удовлетворяющих условиям
, удовлетворяющих условиям 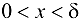 , будет выполнено неравенство
, будет выполнено неравенство 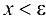 . Поэтому
. Поэтому
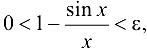
откуда
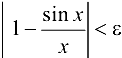
Это означает, что
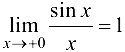
Так как функция 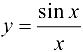 четная, то
четная, то 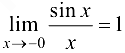 . В силу теоремы 3.2,
. В силу теоремы 3.2, 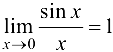 . ■
. ■
Следствие 3.1 *. 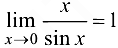 .
.
Пример 3.4.
Доказать, что 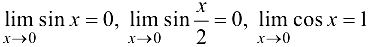
Решение:
1. В процессе доказательства первого замечательного предела получено 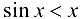 при
при 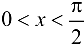 . Очевидно, что
. Очевидно, что 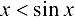 при
при 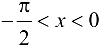 . Тогда
. Тогда 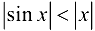 при
при 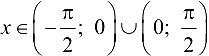 ; Так как для указанных значений
; Так как для указанных значений 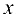 выполнено
выполнено 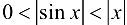 , то переходя к пределу при
, то переходя к пределу при 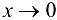 , на основании свойств функций, имеющих предел, получаем
, на основании свойств функций, имеющих предел, получаем 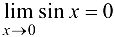 .
.
2. Так как 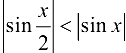 при
при 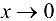 , то
, то 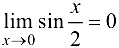 .
.
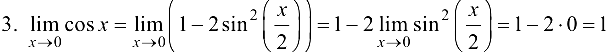
Вывод. Требуемое доказано.
Пример 3.5.
Вычислить 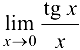 .
.
Решение:
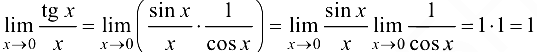
Ответ: 1.
Пример 3.6.
Вычислить 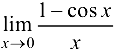 .
.
Решение:
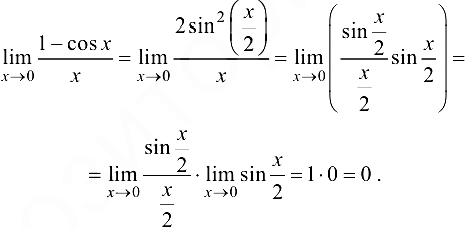
Ответ: 0.
Второй замечательный предел
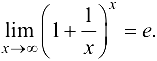
Из теории последовательностей известно, что 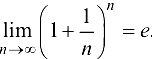 .
.
Пусть 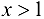 . Положим
. Положим 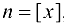 , тогда
, тогда 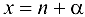 , где
, где 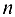 — натуральное число,
— натуральное число, 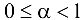 . Так как
. Так как 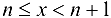 , то
, то 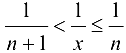 . Тогда
. Тогда
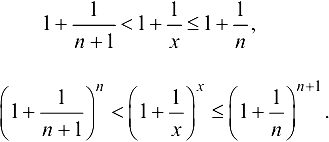
Перейдем к пределу при 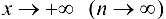 :
:
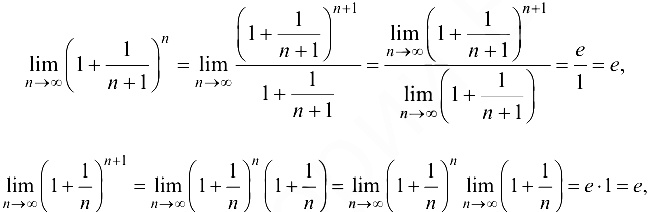
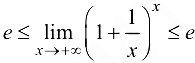 , откуда
, откуда 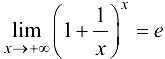 .
.
Пусть 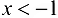 . Положим
. Положим 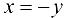 . Тогда
. Тогда
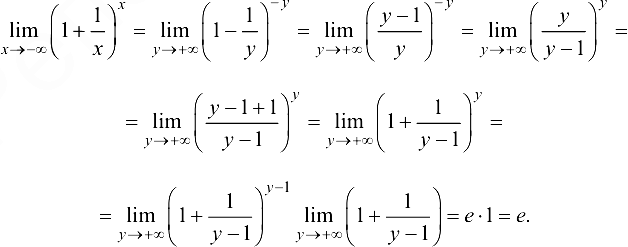
Объединив два случая, получим 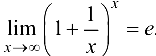 ■
■
Следствие 3.2*. 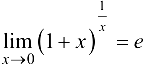 .
.
Пример 3.7.
Вычислить 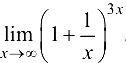 .
.
Решение:
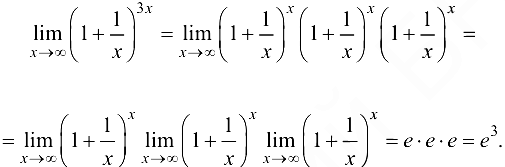
Ответ: 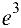 .
.
Пример 3.8.
Вычислить 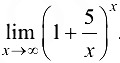 .
.
Решение:
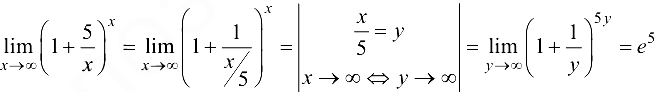
Ответ: 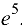
Пример 3.9.
Вычислить 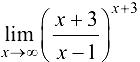
Решение:
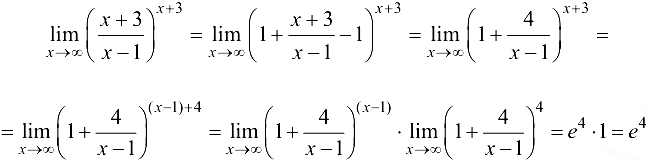
Ответ: 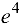 .
.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:

