Оглавление:
Первообразная и интеграл
Из главы 4 нам уже известно, что дифференцирование — это операция нахождения по заданной функции ее производной. Для операции дифференцирования существует обратная операция, называемая интегрированием: отыскание функции по ее производной.
Функция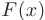 
называется первообразной для 
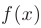на множестве 
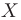, если 
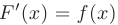для любого 
.
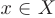Необходимо заметить, что любая непрерывная на 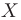функция 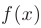имеет первообразную 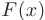на множестве 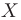и разность между любыми двумя первообразными для 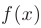равна постоянной величине.
Неопределенным интегралом от функции 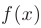на промежутке 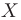называется совокупность всех первообразных этой функции:
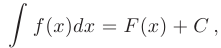
где 
— знак интеграла; 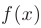— подынтегральная функция; 
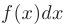— подынтегральное выражение; 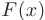— функция, первообразная для функции 
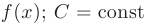— произвольная постоянная.
Свойства неопределенного интеграла
- Производная от неопределенного интеграла равна подынтегральной функции:
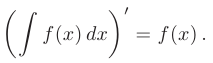
- Дифференциал неопределенного интеграла равен подынтегральному выражению:
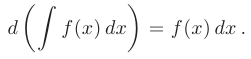
- Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная:
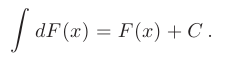
- Постоянный множитель можно выносить за знак интеграла:
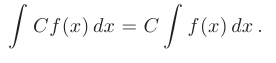
- Неопределенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме неопределенных интегралов от каждого слагаемого:
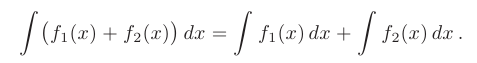
Используя определение неопределенного интеграла и таблицу производных, можно записать таблицу неопределенных интегралов для некоторых элементарных функций.
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Достаточное условие экстремума в математике |
| Наибольшее и наименьшее значения функции в математике |
| Основные методы интегрирования в математике |
| Интегрирование некоторых классов функций в математике |
