Пересечение прямой с плоскостью
Общим элементом пересечения прямой с плоскостью является точка, принадлежащая и прямой и плоскости. Поскольку и прямая и плоскость могут занимать различные положения относительно плоскостей проекций, то при их пересечении также возможны три случая:
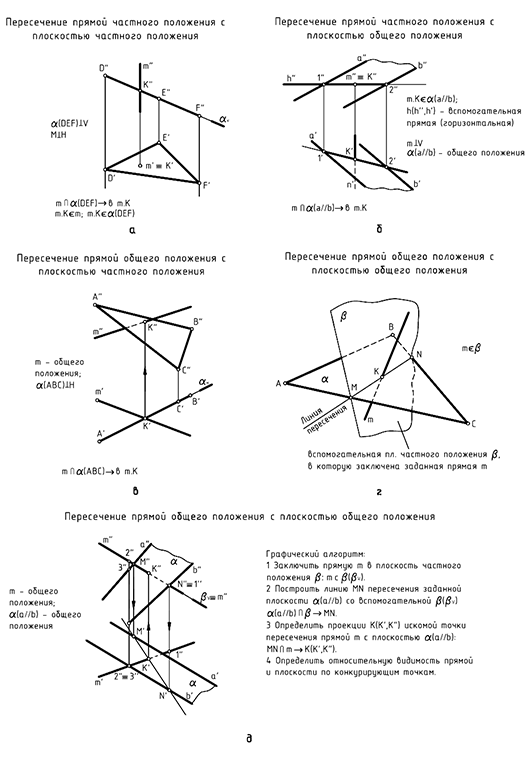
1-й случай — и прямая и плоскость занимают частное положение относительно плоскостей проекций. В этом случае проекции искомой точки пересечения определяются на характерных (вырожденных) проекциях прямой и плоскости.
На рис. 4.4, а изображена горизонтальная плоскость уровня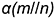 
, пересекающаяся с горизонтально-проецирующей прямой 
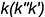. Фронтальная проекция 
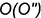точки их пересечения совпадает с фронтальным следом плоскости 
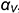, а горизонтальная проекция 
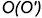точки их пересечения совпадает с вырожденной в точку горизонтальной 
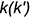проекцией прямой.
2-й случай — только один элемент (или прямая или плоскость) занимает частное положение относительно плоскостей проекций. В этом случае одна из проекций точки пересечения совпадает с характерной (вырожденной) проекцией элемента частного положения, а другую проекцию точки пересечения требуется построить.
На рис. 4.4, б изображены пересекающиеся фронтально-проецирую-щая прямая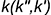 
и плоскость общего положения, заданная треугольником 
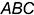. В этом случае фронтальная проекция точки пересечения 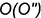совпадает с вырожденной в точку проекцией прямой, а горизонтальная проекция 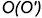точки пересечения построена по принадлежности точки 
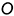плоскости 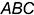с помощью вспомогательной прямой 
.
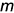3-й случай — оба пересекающихся элемента занимают общее положение относительно плоскостей проекций, то есть пересекается плоскость
общего положения с прямой общего положения. В этом самом сложном для решения случае для построения точки пересечения элементов следует применить вспомогательные построения, чтобы привести условие задачи к более легкому для решения 2-му случаю (см. рис. 4.4), то есть прямую общего положения заменить элементом частного положения, «заключив» эту прямую в плоскость частного положения (см. рис. 3.12 б, в).
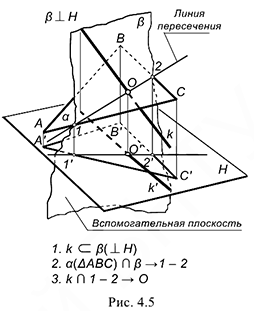
На рис. 4.5 показана наглядная картина этого действия. Прямая общего положения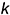 
пересекается с плоскостью общего положения 
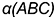. Для решения задачи через прямую проведена некоторая вспомогательная плоскость 
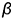, то есть прямая «заключена» в плоскость .
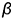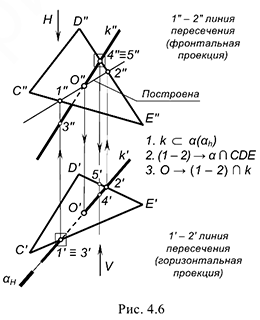
Определяется вспомогательная линия 1-2 пересечения двух плоскостей -заданной и вспомогательной. Искомая точка 
лежит на пересечении за данной прямой к и вспомогательной линии пересечения 1-2.
На рис. 4.6 показано построение на чертеже точки пересечения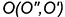 
плоскости общего положения, заданной треугольником 
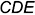, с прямой общего положения 
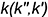. Для решения задачи в этом случае выполняется следующий графический алгоритм (графические действия):
1-е действие. Заключить прямую к во вспомогательную, например горизонтально-проецирующую плоскость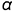 
, задав ее горизонтальным следом 
.
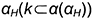2-е действие. Построить проекции вспомогательной линии пересечения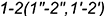 
заданной плоскости 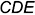со вспомогательной плоскостью 
.
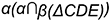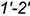совпадает со следом вспомогательной плоскости 
;
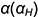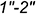строится по принадлежности точек 1 и 2 сторонам 
и 
плоскости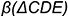 
.
3-е действие. Определить проекции искомой точки пересечения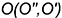 
заданных элементов:
-фронтальная проекция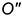 
определяется на пересечении фронтальной проекции заданной прямой к(к») и построенной фронтальной проекции 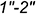вспомогательной линии пересечения ;
;
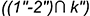- горизонтальная проекция
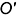определяется на горизонтальной проекции 
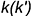заданной прямой по линии связи 
.
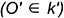4-е действие. Определить на проекциях относительную видимость прямой и плоскости по конкурирующим точкам 1-3 и 4-5.
На рис. 4.6 показано определение относительной видимости заданной прямой 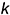и плоскости 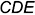с помощью конкурирующих точек, лежащих на скрещивающихся прямых. На горизонтальную проекцию наблюдатель смотрит сверху вниз по стрелке 
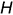. Чтобы определить, какой из элементов -прямая или плоскость — находится ближе к наблюдателю, рассмотрим проекции конкурирующих точек 1 и 3, лежащих на одном проецирующем луче, но на скрещивающихся прямых — точка 1 лежит на прямой , а точка 3 лежит на прямой к. Видно, что ближе к наблюдателю находится точка 1 на прямой , а точка 3 на прямой к расположена ниже. Это значит, что на горизонтальной проекции прямая 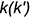вниз от точки пересечения (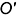) «уходит» плоскость .
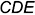Аналогичными рассуждениями, рассмотрев конкурирующие точки 4 и 5 по стрелке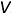 
, определяем относительную видимость прямой и плоскости на фронтальной проекции чертежа — прямая 
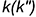находится над плоскостью 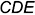вверх от точки .
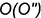Пересечение двух плоскостей общего положения (3-й случай)
При задании пересекающихся плоскостей на чертеже возможны два варианта:
- а) проекции плоскостей в пределах чертежа не накладываются;
- б) проекции плоскостей накладываются.
Для каждого варианта есть разные рациональные способы построения линии пересечения.
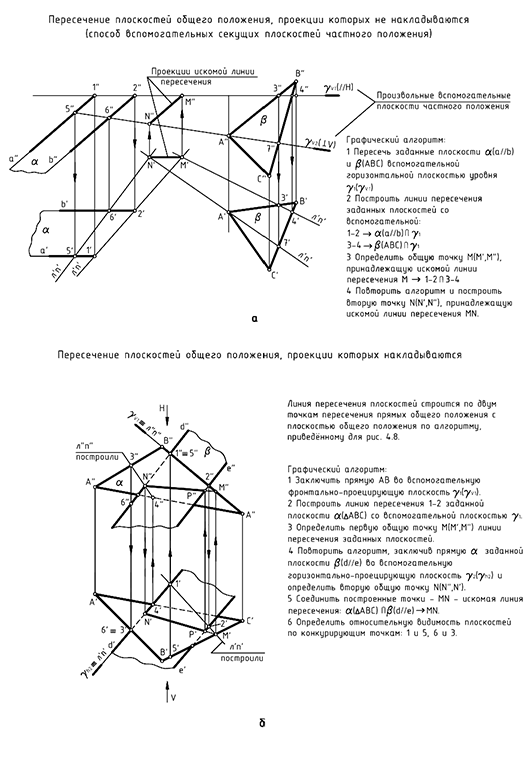
Для варианта «а» рационально использовать две произвольные плоскости частного положения.
На рис. 4.7 показан пример построения линии пересечения плоскостей общего положения —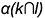 
и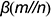 
, проекции которых на чертеже не накладываются.
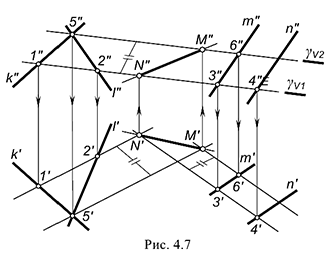
Линия пересечения заданных плоскостей построена по точкам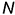 
и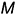 
пересечения между собой вспомогательных линий пересечения этих плоскостей произвольными вспомогательными фронтально-проецирующими плоскостям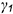и 
и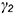 
в соответствии со следующим графическим алгоритмом:
I. Построить точку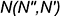 
пересечения заданных плоскосте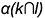й и 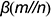вспомогательной горизонтальной плоскостью уровня у
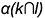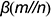1-е действие. Пересечь плоскости и вспомогательной фронтально-проецирующей плоскостью уровня 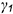и обозначив ее фронтальный след 
.
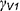2-е действие. Построить проекции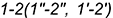 
и 
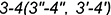вспомогательных линий пересечения заданных плоскосте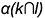й и 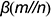вспомогательной плоскостью 
.
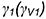3-е действие. Определить проекции точки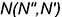 
пересечения между собой вспомогательных лини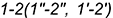й и .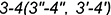
II. Построить точку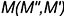 
пересечения заданных плоскосте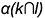й и 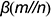вспомогательной фронтально-проецирующей плоскостью 
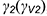, повторив графические действия 1, 2 и 3, и соединить прямой линией построенные точк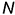и и 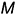. Если при этом плоскость 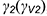задавать параллельно ранее заданной плоскости 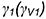, то построения можно упростить и использовать не четыре, а только две точки 5 и 6, так как пересечение параллельными плоскостями будет давать параллельные вспомогательные линии.
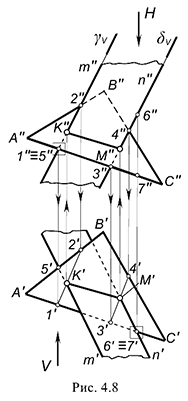
Рассмотрим наиболее часто встречающийся в различных задачах вариант «б» — проекции плоскостей накладываются. Построение проекций линии пересечения сводится здесь к построению точек пересечения двух любых прямых одной плоскости с другой плоскостью, то есть к выполнению дважды графического алгоритма построения точки пересечения прямой общего положения с плоскостью общего положения, изложенного выше (см. рис. 4.6).
На рис. 4.8 показан пример построения линии пересечения плоскостей общего положения —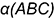 
и 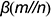, проекции которых на чертеже накладываются.
Линия пересечения построена по точкам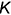 
и 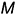пересечения прямых 
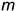и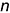 
, которыми задана плоскость 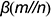, с плоскостью 
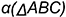, то есть дважды выполнен вышеприведенный графический алгоритм.
I. Построить точку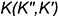 
пересечения прямой 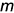с плоскостью ;
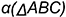1-е действие. «Заключить» прямую 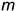во вспомогательную фронтально-проецирующую плоскость 
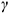и обозначить ее фронтальный след 
.
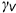2-е действие. Построить проекции 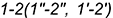вспомогательной линии пересечения плоскостей — заданной 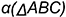со вспомогательной .
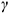3-е действие. Определить проекции точки 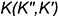пересечения прямой 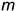с плоскостью .
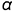II. Построить проекции точки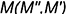 
пересечения прямой 
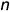с плоскостью 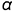, повторив графические действия 1, 2 и 3 и соединить прямой линией построенные точк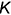и и .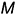
4-е действие. Определить видимость плоскостей относительно построенной линии пересечения 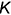—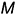, рассмотрев пары конкурирующих точек:
- точки 1 и 5 — для определения относительной видимости на фронтальной проекции;
- точки б и 7 — для определения относительной видимости на горизонтальной проекции.
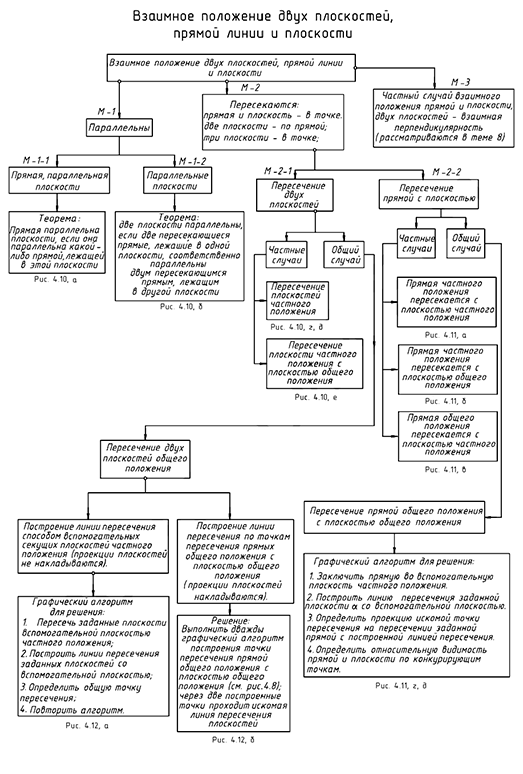
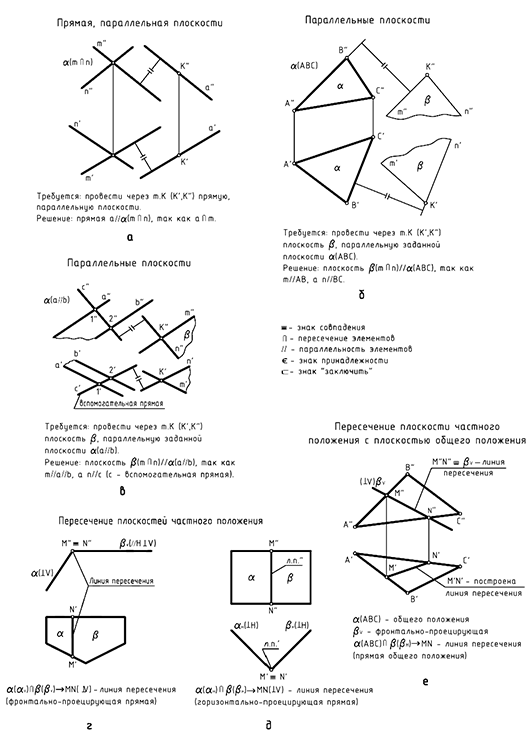
Структуризация материала четвертой лекции в рассмотренном объеме схематически представлена на рис. 4.9 (лист 1). На последующих листах 2-4 компактно приведены иллюстрации к этой схеме для визуального закрепления основной части изученного материала при повторении (рис. 4.10-4.12).
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Начертательная геометрия для 1 курса
Возможно эти страницы вам будут полезны:
| Понятие о следах плоскости |
| Взаимное положение двух плоскостей, прямой линии и плоскости |
| Перпендикулярность |
| Способ замены (перемены) плоскостей проекций |
