Переход от алгебраической формы к тригонометрической и показательной.
Для того чтобы осуществить переход от алгебраической формы к тригонометрической и показательной, будем использовать следующий алгоритм:
- Выделите параметры а и b в алгебраической форме
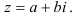 .
. - Найдите модуль комплексного числа
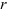 по формуле:
по формуле: 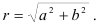 .
. - Для нахождения аргумента
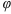 выполните вспомогательный чертеж и определите четверть, в которой расположен вектор
выполните вспомогательный чертеж и определите четверть, в которой расположен вектор 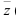 (а, следовательно, и угол
(а, следовательно, и угол 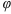 ).
). - В зависимости от четверти, в которой лежит угол
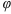 , воспользуйтесь одной из следующих формул:
, воспользуйтесь одной из следующих формул:
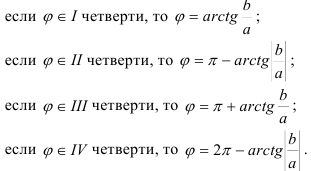
Подставьте найденные значения 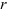 и
и 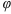 в тригонометрическую и показательную формы.
в тригонометрическую и показательную формы.
Пример решения заказа контрольной работы №128.
Переведите комплексное число 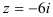 в показательную и тригонометрическую формы.
в показательную и тригонометрическую формы.
Решение:
Выделим параметры 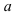 и
и 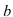 в алгебраической форме
в алгебраической форме
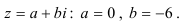
Найдем модуль комплексного числа 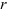 по формуле
по формуле
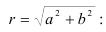
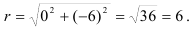
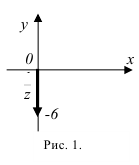
Для нахождения аргумента 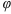 выполним вспомогательный чертеж (рис. 1). Видим, что полученный вектор образует с положительным направлением оси
выполним вспомогательный чертеж (рис. 1). Видим, что полученный вектор образует с положительным направлением оси 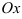 угол
угол 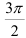 , следовательно, без применения дополнительных формул делаем вывод, что
, следовательно, без применения дополнительных формул делаем вывод, что 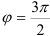 .
.
Так как
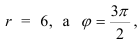
то тригонометрическая форма комплексного числа имеет вид:
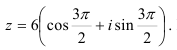
Показательная форма того же числа равна
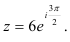
Ответ:
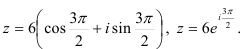
На этой странице вы сможете заказать контрольную работу и познакомиться с теорией и другими примерами решения:
Заказать контрольную работу по высшей математике
Другие похожие темы возможно вам будут полезны:

