Оглавление:
Пассивные идеальные элементы
Идеальный резистор
Идеальному резистору приписывается одно физическое свойство -оказание сопротивления 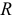 постоянному току
постоянному току 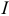 с преобразованием электрической энергии в тепловую.
с преобразованием электрической энергии в тепловую.
В соответствии с законом Ома:

где 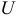 — падение напряжения на идеальном резисторе.
— падение напряжения на идеальном резисторе.
На рисунке 2.1 представлено изображение идеального резистора. Направление стрелки тока выбрано произвольно, но направление стрелки падения напряжения выбирают всегда совпадающим со стрелкой тока и часто ее не ставят на схеме.

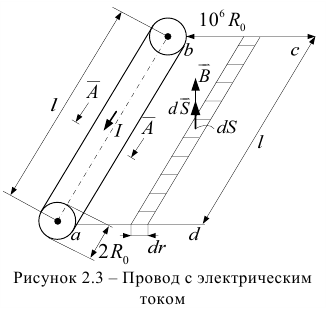
Физическая природа сопротивления металлов току обусловлена наличием свободных электронов, которые могут легко перемещаться между ионами, находящимися в узлах кристаллической решетки и совершающих колебательное движение. Пока в проводнике отсутствует электрическое поле, электроны беспорядочно движутся во всевозможных направлениях.
При возникновении поля электроны начинают медленно перемещаться по направлению, противоположному направлению силовых линий поля. Скорость хаотического перемещения электронов проводимости при комнатных температурах 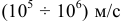 , а скорость направленного движения электронов
, а скорость направленного движения электронов 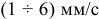 . Это медленное перемещение (дрейф) практически не влияет на тепловое движение электронов проводимости.
. Это медленное перемещение (дрейф) практически не влияет на тепловое движение электронов проводимости.
Не следует смешивать скорость дрейфа электронов со скоростью распространения электромагнитной волны тока. Опыт и теория показывают, что ее величина может достигать скорости света. Энергию от источника к потребителю передает электромагнитное поле, проводник же с дрейфующими электронами служит лишь «направляющей» для потока энергии.
Удельное сопротивление металла в соответствии с электронной теорией, определяется выражением:

где 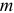 — масса электрона;
— масса электрона; 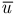 — тепловая скорость электрона;
— тепловая скорость электрона; 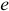 — электрический заряд электрона;
— электрический заряд электрона; 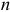 — концентрация свободных электронов;
— концентрация свободных электронов; 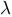 — средняя длина свободного пробега электрона между двумя столкновениями.
— средняя длина свободного пробега электрона между двумя столкновениями.
В соответствии с дифференциальной формой закона Ома:

где 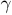 — удельная проводимость;
— удельная проводимость;  — напряженность электрического поля;
— напряженность электрического поля; 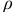 — удельное сопротивление.
— удельное сопротивление.
Т.е. сопротивление току в проводниках зависит от взаимодействия (столкновения) свободных электронов с ионами кристаллической решетки, характеристиками электронов и их концентрацией.
Идеальная катушка индуктивности
В пункте 1.3.2 дана количественная мера идеальной катушки индуктивности: это индуктивность 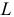 , определяемая как отношение магнитного потокосцепления катушки к величине тока
, определяемая как отношение магнитного потокосцепления катушки к величине тока 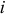 в ней. Т.е. идеальной катушке индуктивности приписывают только одно физическое свойство: наличие магнитного потокосцепления, созданного током
в ней. Т.е. идеальной катушке индуктивности приписывают только одно физическое свойство: наличие магнитного потокосцепления, созданного током 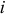 в этой катушке или коэффициента
в этой катушке или коэффициента 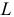 самоиндукции, величина которого пропорциональна абсолютной магнитной проницаемости
самоиндукции, величина которого пропорциональна абсолютной магнитной проницаемости 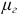 , квадрату числа витков и площади
, квадрату числа витков и площади 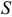 витков (1.32); преобразования электрической энергии в тепловую энергию не происходит, а происходит только запасание энергии магнитного поля.
витков (1.32); преобразования электрической энергии в тепловую энергию не происходит, а происходит только запасание энергии магнитного поля.
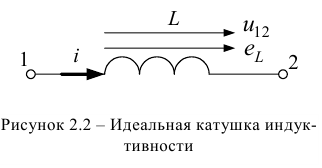
На рисунке 2.2 представлено условное обозначение идеальной катушки индуктивности и проставлены условно положительные направления тока 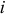 , напряжения
, напряжения 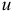 и ЭДС самоиндукции
и ЭДС самоиндукции 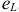 .
.
Связь между током и напряжением в индуктивном элементе устанавливается на основе закона электромагнитной индукции, т.е. выразим потенциал точки 1 через потенциал точки 2 и ЭДС:
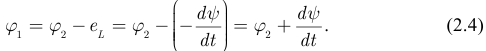
Следовательно:
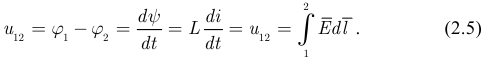
При постоянном токе в катушке индуктивности ток не изменяется, значение производной равно нулю, следовательно, 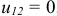 , что указывает на отсутствие работы при перемещении единичного положительного заряда от точки 1 до точки 2, выполняемой источником энергии электрической цепи. Т.е. катушка индуктивности сопротивления постоянному току не оказывает, что равносильно короткому замыканию выводов.
, что указывает на отсутствие работы при перемещении единичного положительного заряда от точки 1 до точки 2, выполняемой источником энергии электрической цепи. Т.е. катушка индуктивности сопротивления постоянному току не оказывает, что равносильно короткому замыканию выводов.
Физическая природа силы сопротивления электрическому току катушки индуктивности связана с величиной скорости изменения во времени магнитного потокосцепления или при 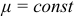 (линейной катушки) с величиной
(линейной катушки) с величиной 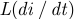 .
.
Мгновенная мощность идеальной катушки индуктивности:

При совпадении знаков 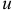 и
и 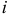 происходит запасание энергии и мощность положительна. При отрицательной мощности элемент отдает энергию.
происходит запасание энергии и мощность положительна. При отрицательной мощности элемент отдает энергию.
Если 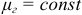 , то
, то 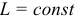 , такая идеальная катушка индуктивности называется линейной. При
, такая идеальная катушка индуктивности называется линейной. При 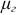 зависящей от величины напряженности магнитного поля
зависящей от величины напряженности магнитного поля 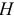 , т.е. наша величина
, т.е. наша величина 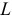 зависит от величины
зависит от величины 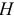 или
или 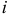 , т.е.
, т.е. 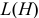 и такую катушку индуктивности называют нелинейной.
и такую катушку индуктивности называют нелинейной.
Для случая линейной идеальной катушки индуктивности энергия магнитного поля определяется выражением:
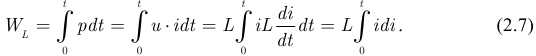
Если 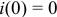 , то:
, то:
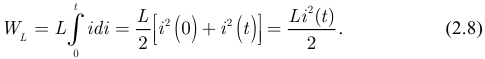
Энергия не может принимать отрицательных значений.
Идеальный конденсатор
В параграфе 1.1.1 уже рассматривалось понятие емкости одного заряженного тела. В данном параграфе рассмотрим емкость двух проводящих заряженных тел разделенных диэлектриком.
Электрическая емкость вообще характеризует свойство проводящих тел заряжаться под влиянием электрического поля, а также накапливать в поле этих тел электрическую энергию.
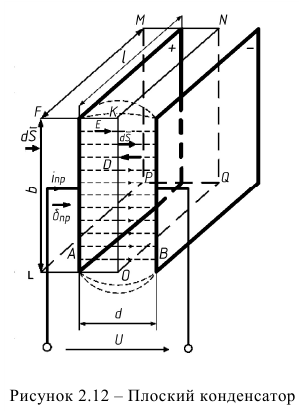
Конструктивно конденсаторы представляют собой две пластины, называемые обкладками (рисунок 2.12). Обкладки разделены диэлектриком. Их заряжают, присоединив к разноименным зажимам одного источника.
Тогда заряды этих тел будут равны по величине и противоположны по знаку (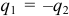 , причем
, причем 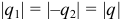 ). Образование зарядов на двух телах в этом случае можно рассматривать как перенос электронов с тела, заряжаемого положительно, на тело, заряжаемое отрицательно. Заряд каждого тела будет пропорционален разности потенциалов
). Образование зарядов на двух телах в этом случае можно рассматривать как перенос электронов с тела, заряжаемого положительно, на тело, заряжаемое отрицательно. Заряд каждого тела будет пропорционален разности потенциалов 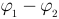 :
:

Тогда:

следовательно, емкость численно равна отношению заряда одного из тел к разности потенциалов между ними. Емкость системы в этом случае, как и в случае уединенного проводника, зависит от формы, размеров, поверхности тел, их взаимного расположения, а также от диэлектрической проницаемости среды 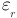 .
.
При постоянном значении всех перечисленных величин, от которых зависит потенциал тел, величина 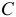 также постоянна. В общем случае, когда все эти величины под влиянием каких-либо причин изменяются, емкость не остается постоянной.
также постоянна. В общем случае, когда все эти величины под влиянием каких-либо причин изменяются, емкость не остается постоянной.
Идеальным конденсатором будем называть устройство, состоящее из двух проводящих пластин, разделенных диэлектриком, для которого учитывают только емкость 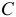 (способность накапливать заряды) и энергию в электрическом поле.
(способность накапливать заряды) и энергию в электрическом поле.
Свойством проводимости тока диэлектриком (электронной, ионной и т.д.) с преобразованием электрической энергии в тепловую пренебрегают, как и наличием коэффициента самоиндукции и взаимной индукции. Другими словами: 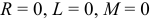 .
.
Величина тока в идеальном конденсаторе обусловлена исключительно величиной плотности тока электрического смещения 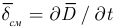 , где
, где 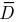 — вектор электрического смещения. Если охватить одну из обкладок замкнутой поверхностью в виде параллелепипеда (рисунок 2.12), то в соответствии с первым законом Кирхгофа:
— вектор электрического смещения. Если охватить одну из обкладок замкнутой поверхностью в виде параллелепипеда (рисунок 2.12), то в соответствии с первым законом Кирхгофа:
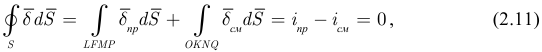
где 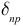 — плотность тока проводимости.
— плотность тока проводимости.
Следовательно: 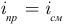 .
.
Когда по проводнику, пересекающему поверхность 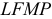 направлен к обкладке ток проводимости
направлен к обкладке ток проводимости 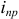 в диэлектрике образуется ток смещения, проходящий сквозь поверхность
в диэлектрике образуется ток смещения, проходящий сквозь поверхность 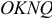 изнутри наружу в точности равный току
изнутри наружу в точности равный току  в проводнике. Линии тока смещения в диэлектрике являются продолжением линий тока в проводнике. Таким образом, цепь электрического тока является замкнутой.
в проводнике. Линии тока смещения в диэлектрике являются продолжением линий тока в проводнике. Таким образом, цепь электрического тока является замкнутой.
Величина тока  численно равна количеству электрических зарядов, пересекающих сечение проводника в единицу времени. Очевидно, на токае же количество зарядов в единицу времени должен измениться заряд
численно равна количеству электрических зарядов, пересекающих сечение проводника в единицу времени. Очевидно, на токае же количество зарядов в единицу времени должен измениться заряд  пластины:
пластины:

где 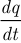 — скорость изменения заряда
— скорость изменения заряда 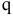 .
.
Если напряжение источника энергии изменяется по синусоидальному закону 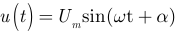 , то:
, то:

Амплитуда синусоидального тока:

где 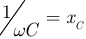 — сопротивление конденсатора синусоидальному току.
— сопротивление конденсатора синусоидальному току.
Соотношение (2.14) называют законом Ома для амплитудных значений тока и напряжения на конденсаторе.
В соответствии с формулами (2.12) и (2.14) можно сказать, что величина сопротивления идеального конденсатора току обратно пропорциональна произведению величины емкости и скорости изменения напряжения на конденсаторе.
Для постоянного напряжения и тока идеальный конденсатор оказывает бесконечное сопротивление.
Таким образом, физическая природа сопротивления идеальных пассивных элементов (резистора, катушки индуктивности и конденсатора) существенно различна.
Эта страница взята со страницы задач по электротехнике:
Электротехника — решения задач и примеры выполнения заданий
Возможно эти страницы вам будут полезны:

