Параболическая формула

Параболическая формула

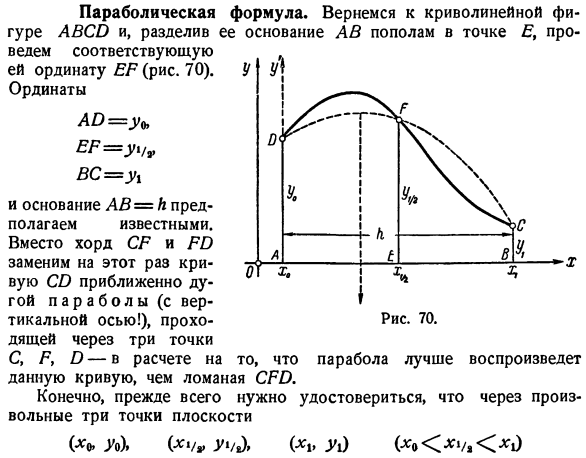
Параболическая формула. Вернитесь к кривой рис. ABCG>, разделите базовую точку AB пополам с точкой E и нарисуйте соответствующую ординату EE (рис.70). Рукоположение Ай = гг ВП = yhr до н. э. = У1 А основание AB = H предполагается известным. Вместо кода CE и Her, на этот раз мы заменим кривую CO почти параболической дугой(с вертикальной осью).Пройдите через 3 точки. C, E, O-в надежде, что парабола воспроизведет эту кривую лучше, чем сломанный гендиректор. Конечно, первым делом нужно обязательно пройти через любые 3 точки плоскости ( * » .(*/«Г ’/ а)> ( * / .Ыы）（* 0 ’ /、！> На самом деле, такая парабола может быть выполнена всегда, и даже только на 1 больше. Форма параболического уравнения с вертикальной осью имеет вид у = ах * ВХ + с、 И его коэффициент однозначно определяется из следующих 3 условий: топор \ + + с = У1 0 * 1/,+&*!/ , + с = = У1 /、 х \ \ bx1-\ с = Йи.

Формула (4), дающая точное значение площади под параболой, приблизительно воспроизводит только искомую площадь под кривой. Людмила Фирмаль

• Системные детерминанты * 0 * 0 1 !/ , XChx 1 1 («Матрица вандермонда») ненулевая). Затем вычислите площадь P фигуры, которая окружена сверху дугой параболы. Эта область представлена следующей формулой, как показано на рисунке +(4） Обычно ассоциируется с именем Симпсон**). Без потери общности можно предположить, что ось y проходит через точку A. Один Р = | (ах * + * м; -) с)^ = |(2aH * + 3к + 6С). Да. И я думаю, что Г * = с, 4 + + ый = Ак *\ ьк-\ с、 После этого, формула Симпсона проверяется непосредственно. y = f (x). б ^ /(х) топор == ^(г,+ 4г, Ф+ М».). (5） *) при a = 0 парабола вырождается в прямую линию. ** ) Томас Симпсон (1710-1761) английский математик.

• Видимо, формула была известна и до него. Сделайте то же самое, что и выше, чтобы улучшить точность. Сначала разделите интервал[a, b]на n равных частей (1)и разделите рассматриваемую фигуру на n полос. Это выражение использует среднюю ординату в дополнение к экстремуму, поэтому оно используется для x x / / #lga / y …, xn_1 / 9 половинные точки должны использоваться для разделения каждого из n частичных интервалов(1) (в общей сложности основной разрыв будет разбит на 2 части).Все я(не 2л!) Основание полосы-равно, поэтому для площади получается соответствующая приближенная формула. ^ 0 + 4-Y»/, + Y) > ^О ’ -! + БН-ХС + уя Если вы их добавите, то получите новую приблизительную формулу. Ф(Х) & Х ^ [КР + гг)+ 2(у \ + … + Ля+)* + 4 Су * / * + * * * +Ул —/).

Эта формула чаще используется для приближенного вычисления интеграла, чем трапециевидная формула. Людмила Фирмаль

• Для сравнения снова вычислите Интеграл По формуле Простота Это называется параболическим или уравнением Симпсона. Это связано с тем, что одна и та же трудоемкость обычно дает более точный результат. Ага. 1 + L：* Пойти спать. Поскольку используется 2n = 4, число декартовых координат, используемых на этот раз, еще меньше, чем раньше. Есть 5 признаков для расчета. *. = ° * * / , = Т 1 х -2 3 1 * ’ / * = т Y,= 1 4″!/ , = 3.76471 23 ^ 1.6 4uv / 1 = 2.59 y * = 0.5 1（1 + 3.76471 + 1.6 + 2.56 + 0.5）= 0.78539… 5 символов все правильно! Конечно, в отношении формулы (5)можно повторить замечания, упомянутые в конце предыдущего выпуска. Затем оцените погрешность приближенной формулы.

Смотрите также:

Решение задач по математическому анализу

Формула Валлиса.	Дополнительные члены приближенных формул.
Формула трапеций.	Определение понятия площади.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.