Оглавление:


Отыскание максимального и минимального значений функции, определенной на сегменте.
- Найдите максимальное и минимальное значения функций, определенных для сегмента. Рассмотрим функцию y=f (x), которая определена в отрезке[a, B]и смежна на нем. До сих пор я искал только
локальный максимум и минимум функции. Здесь мы ставим задачу нахождения глобальных максимумов и минимумов, или,
по-другому, задачу нахождения F (x) максимумов и минимумов отрезков[a, B]. Людмила Фирмаль
Остановимся на теореме Вейерштрасса (см. 4.15 Главу 4), чтобы найти F (x) максимумы отрезков[a, B]для уверенности, что непрерывная функция f (x) обязательно достигает своего максимума (минимума) в некоторой точке отрезка[a, B]. Максимальное значение функции f (x)
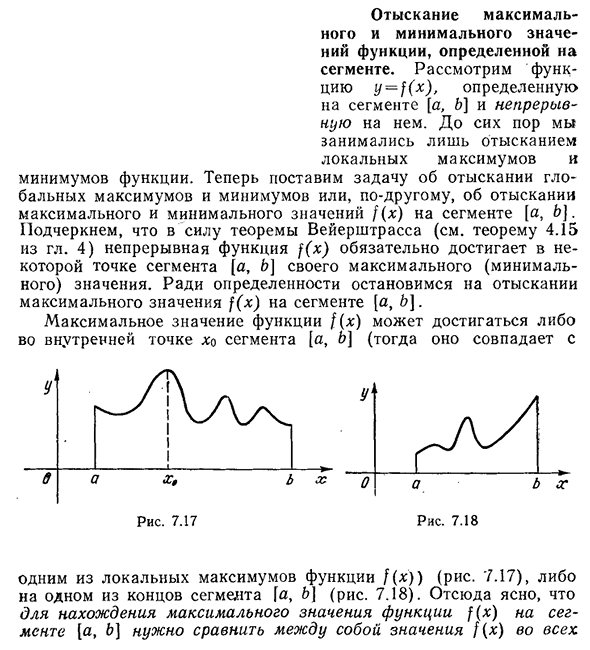
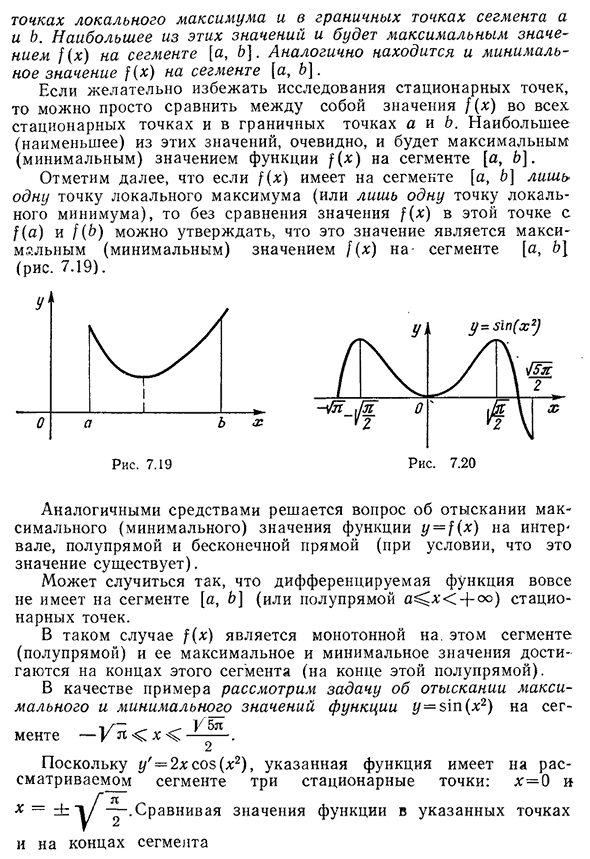
может быть достигнуто в любой из точек XO внутри отрезка[a, B] (совпадает со следующим Один из максимумов функции/(*)) (рис. 7.17), или на одном конце сегмента[a,&] (рис. 7.18). Итак, чтобы найти максимальное значение функции f (x) на отрезке[a, B], ясно, что во всех§6 необходимо сравнить значения функции f (x). Краем полюса
- 285 Наибольшее из этих значений-максимальное значение f (x) в сегменте[a,&]. Аналогично, мы находим наименьшее значение f (x) в отрезке[a,B]. Если желательно избежать изучения стационарных точек, то можно просто сравнить значения f (x) во всех стационарных точках и граничных точках a и B. Кроме того, если f (x) находится на
отрезке, можно сравнить f (a) и f (b) в этой точке, не сравнивая значение f (x) с локальным максимумом (или только одной точкой на локальном минимуме) 7.19). Аналогично решается задача нахождения максимума (минимума) функции y=f (x) в межвалковых, полупрямоугольных и бесконечных линиях (при условии, что эта величина существует). Дифференцируемой функции может не иметь неподвижной точки На отрезке[а,&](или полу-непосредственно
в^Х<4 -°). В таких случаях f (x)монотонно.Этот сегмент (полупрямой) и его Людмила Фирмаль
максимальные и минимальные значения достигают обоих концов этого сегмента (конца этого сегмента). В качестве примера рассмотрим задачу нахождения максимального и минимального значений функции y=sin (x2) mente—<x<. Поскольку Y’=2xcos (x2), указанная функция возвращает значение указанной функции и значение функции на обоих концах сегмента в проблемном сегменте, который сравнивается с x -±. Сэг-на РАС-х=0 и точках286гл. 7. Рассмотрим график функции /(0) = 0, = / ( _ |L P)=O, Убедимся, что
максимальное значение рассматриваемой функции равно+1 и достигает в двух внутренних точках отрезка:XG= — и x2=|/и минимального значения. , / 2 ^Рассматриваемой функции равна——и достигается справа Конец 5-литрового сегмента — — -. График функции показан на рисунке. 7.20
Смотрите также:

