Относительный покой жидкости и (равновесие) жидких сред

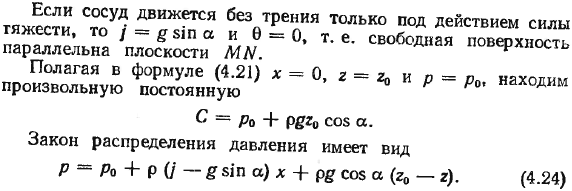
Относительный покой жидкости.

Относительный покой жидкости. Состояние, в котором жидкость неподвижна относительно стенок резервуара, движущегося с постоянным ускорением относительно Земли, обычно называют относительным неподвижным. Если вы выберете систему координат, плотно связанную со стенками резервуара, то вы попадете в статическую задачу. Это лежит в основе решения, которое представляет собой уравнение Эйлера (4.1). в соответствии с известным принципом механики, при использовании уравнений равновесия в движущейся системе координат с ускорением необходимо включать инерционные силы в число сил рабочей массы. Имея это в виду, мы рассмотрим 2 случая относительного равновесия. 1.Равновесие жидкости в цилиндрическом контейнере, который равномерно вращается вокруг вертикальной оси.

Рассмотрим состояние жидкости в контейнере после того, как прошло достаточное количество времени с момента начала вращения, когда был достигнут относительный покой(рис.4.4, а). Людмила Фирмаль

• Выберите оси, как показано на рисунке. 4.4 применяет дифференциальные уравнения гидродинамики вида С и (4.9)к жидкости. К числу массовых сил, связанных с гравитацией Р8 -%, необходимо отнести центробежную инерцию Рас =(0 ″ т°=© * н° ° 、 Где V-окружная скорость частицы жидкости в любой точке M(x, y), r-радиус вращения частицы, r° радиальный единичный вектор. со-угловая скорость контейнера. Для проекции на координатные оси результирующих массовых сил получим формулу П= С05(р, х) = в COS(р, х) = ИРП.

Шестьдесят восемь Пы = «(г, х)= » 51p позволяют вести съемку быстро В(Г, Х)= ж * п; Р,~ 6Подставляя эти выражения в Формулу (4.9), y = u * (*01x-b y yu § y или у-+ А-80° После интегрирования, находим П = п-х (^ * + «*) р ^ + с.(4.17)） Если положить p = * const из Формулы (4.17), то получим уравнение изотропной плоскости р(х * + г%) п#2 + с » =0.(4.18)） Как видно из Формулы (4.18), эти поверхности являются вращательными параболами, совпадающими с осью z, и 1 из таких парабол является свободной поверхностью жидкости.

• Координаты вершины параболоида свободной поверхности даны в r0 (рис. 4.4, а). в вершине x = y-0 уравнение свободной поверхности по формуле (4.18) будет иметь следующий вид, так как оно Cg» » rdgo n: + 0 «•» Если внешнее давление равно p0, то в Формуле (4.17) найти константу C =p1 + pgr0, установив p = «p0, x = y = 0, 2 * = 20.Закон распределения давления может быть выражен следующей формулой П = По + П8 (»*+р» р] (4.20） Для любой точки M с координатами x, y, r выражение в скобках это втягивание точки M ниже свободной поверхности, a. как это Р-ры + РБИ. То есть действует линейный (гидростатический) закон распределения давления в глубинном направлении, в данном случае он измеряется от искривленной свободной поверхности. 2.Равновесие жидкости в сосуде движется линейно с постоянным ускорением. Рассмотрим равновесие жидкости в сосуде, которая движется с ускорением а по наклонной прямой как с углом к горизонту.

Шестьдесят девять а-поворот вокруг вертикальной оси. о-двигаться линейно с постоянным ускорением Скрап а(рис. 4.4, б). помимо силы тяжести в этом случае в силу массы входит сила инерции Р1—а=/. Людмила Фирмаль

• Это противоречит ускорению судна.4.4 B в системе координат, показанной на рисунке, проекция массовой силы РХ = 1 § 3; ру = 0; пр =& коза. Подставляя эти уравнения в уравнение равновесия (4.9)、 (1 / р) Ар-Ш-8 8 {Н») А-Д сөз яе]、 После интеграции Р = p 0 ’-8 51p позволяют вести съемку быстро а) х-й, потому что А-Г + С.(4.21） Предполагая p-константу уравнения(4.21), получаем уравнение изобарной плоскости. П (1-8 ы * н а)х-й потому что-г + УП = 0(4.22） Р-Р0 = ]д ЗШ и кос (4.23） Формула (4.22) дает ряд плоскостей, параллельных оси Y.1 из этих плоскостей являются свободными гранями.

Обозначим координаты пересечения свободной поверхности и оси r через r0 и подставим x = 0 и r = r0 в Формулу (4.22), чтобы найти-rdgo co8 свободной поверхности. Форма уравнения для этой поверхности имеет вид Куда? /-#8} Р06; При COS 70 Если корабль движется без трения только под действием силы тяжести, то/ = § $ » a и 0 = 0, то есть свободная поверхность параллельна плоскости WE. Принимая формулу (4.21) x = 0, r =и p = p0, находим произвольную константу С = Р0 + Р8 * ОО долл. Форма закона распределения давления П-по + ПК-8 5 * н а) х + РД потому что(рН-Р).

Смотрите также:

Примеры решения задач по гидравлике

Возможно эти страницы вам будут полезны:

1. Уравнения эйлера для покоящейся жидкости и их интегрирование.
2. Основная формула гидростатики. закон паскаля. понятие о напоре.
3. Силы давления жидкости на твердые поверхности.
4. Обобщенная гипотеза ньютона о связи между напряжениями и скоростями деформаций.