Основные законы электрических цепей
При описании геометрической структуры схем замещения электрических цепей используют такие топологические понятия, как ветвь, узел, путь, контур, двухполюсник, четырехполюсник, последовательное и параллельное соединения, звезда, треугольник. Схема замещения электрической цени (схема цепи или просто схема) состоит из идеальных активных и пассивных элементов и идеальных соединительных проводников.
Идеальный проводник — проводник любой длины, имеющий нулевое сопротивление. При конечной величине тока напряжение на зажимах идеального проводника также равно нулю. Сопротивление реальных проводников может быть значительным, особенно при большой протяженности (линии передачи энергии или информации). На схемах замещения сопротивление таких проводников учитывают в виде сопротивления, встроенного в идеальный проводник.
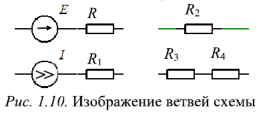
Участок схемы, по которому протекает один и тот же ток, называется ветвью. Ветвь образуется одним или несколькими последовательно соединенными элементами цепи (рис. 1.10). Активная ветвь содержит источники электрической энергии, пассивная не содержит.
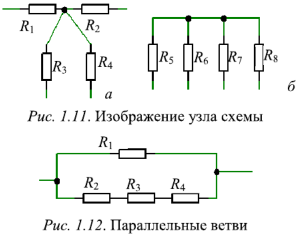
Место соединения трех и более ветвей называется неустранимым узлом (рис. 1.11). Линии, связывающие ветви в схеме (рис. 1.11 ,6), представляют собой идеальные проводники. Поэтому представленные на рис. 1.11,а и рис. 1.11,6 схемы в электрическом смысле одинаковы. Каждая из них содержат один узел и 4 ветви. Узел, в котором сходятся две ветви, называется простым (устранимым).
Ветви, присоединенные к одной паре узлов, называются параллельными (рис. 1.12).
На рис. 1.13 приведена схема, содержащая четыре узла (1, 2, 3, 4) и семь ветвей. Каждая ветвь характеризуется собственным током. Ветви 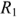 и
и 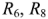 и
и 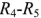 являются параллельными. Ветвь
являются параллельными. Ветвь 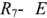 является активной, все остальные ветви являются пассивными.
является активной, все остальные ветви являются пассивными.
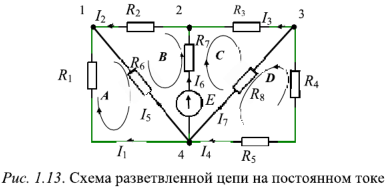
Контур — любой замкнутый путь, образованный несколькими ветвями. Если начать движение по контуру из некоторого узла, то после обхода всех элементов контура придем к исходному узлу. Контуры на схемах отмечают изогнутой стрелкой, показывающей направление обхода контура. На рис. 1.13 показаны четыре контура 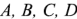 . Каждый из них не содержит внутри другие контуры. Такие контуры называют окнами (ячейками).
. Каждый из них не содержит внутри другие контуры. Такие контуры называют окнами (ячейками).
Первый закон Кирхгофа — в любой момент времени алгебраическая сумма токов всех ветвей, подключенных к узлу, равна нулю:

где 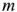 — количество ветвей, сходящихся в рассматриваемом узле. При этом, положительными считаются токи, текущие к узлу, а отрицательными — токи, текущие от узла.
— количество ветвей, сходящихся в рассматриваемом узле. При этом, положительными считаются токи, текущие к узлу, а отрицательными — токи, текущие от узла.
В схеме, изображенной на рис. 1.13, уравнение первого закона Кирхгофа для узла 4 имеет следующий вид:  .
.
Второй закон Кирхгофа — для произвольного замкнутого контура в любой момент времени алгебраическая сумма ЭДС источников напряжения контура равна алгебраической сумме напряжений всех остальных его элементов:

где 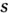 — количество ЭДС в контуре,
— количество ЭДС в контуре, 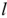 — число остальных элементов контура.
— число остальных элементов контура.
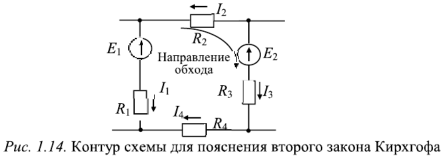
Перед составлением уравнения нужно для всех пассивных элементов контура выбрать положительные направления напряжений (согласованные с направлением токов). Затем выбирают произвольно направление обхода контура. ЭДС, направления которых совпадают с направлением обхода, записывают в левой части равенства со знаком «плюс», а ЭДС, направленные против направления обхода, — со знаком «минус».
В правой части уравнения считают положительными напряжения на элементах тех ветвей, для которых направление обхода и выбранное направление положительного тока совпадают. В противном случае напряжения записываются со знаком «минус».
Применительно к контуру, показанному на рис. 1.14, второй закон Кирхгофа можно записать как 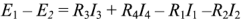 .
.
Закон Ома в простейшем случае связывает величину тока через сопротивление 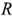 с величиной этого сопротивления и величиной приложенного к нему напряжения
с величиной этого сопротивления и величиной приложенного к нему напряжения 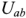 (рис. 1.15):
(рис. 1.15):

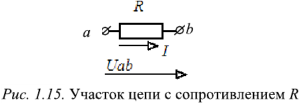
Обобщенный закон Ома устанавливает связь тока и напряжения активной ветви:
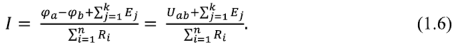
Здесь 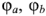 — потенциалы крайних точек ветви,
— потенциалы крайних точек ветви, 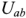 — равное разности потенциалов
— равное разности потенциалов 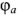 и
и 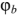 напряжение ветви,
напряжение ветви, 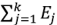 — алгебраическая сумма ЭДС,
— алгебраическая сумма ЭДС, 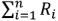 арифметическая сумма сопротивлений участка цепи.
арифметическая сумма сопротивлений участка цепи.
Двухнолюсник (четырехполюсник) — участок цепи, имеющий два (четыре) внешних зажима (полюса), которыми он подключается к остальной цени. На рис. 1.16 изображены в виде прямоугольников активный двухполюсник 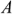 и пассивный четырехполюсник
и пассивный четырехполюсник 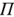 . Рассмотренные элементы (пассивные и активные) являются двухполюсниками. Они имеют два внешних зажима (полюса).
. Рассмотренные элементы (пассивные и активные) являются двухполюсниками. Они имеют два внешних зажима (полюса).
Эта теория взята со страницы помощи с заданиями по электротехнике:
Возможно эти страницы вам будут полезны:
| Пассивные элементы электрической цепи |
| Источники электрической энергии |
| Эквивалентные преобразования пассивных участков электрической цепи |
| Расчет цепей методом эквивалентных преобразований |

