Основные явления электромагнитного поля, применяемые в теории электрических цепей
Поле неподвижных электрических зарядов называют электростатическим нолем, являющимся наиболее простым случаем электромагнитного поля. В обычных условиях в достаточно большом элементе объема тела находятся в среднем равное количество положительно и отрицательно заряженных частиц или, другими словами, положительных и отрицательных электрических зарядов, и тело является электрически нейтральным.
В электрически заряженном теле преобладают положительные или отрицательные заряды. Электрически заряженные тела и частицы окружены электрическим полем, в общем случае изменяющемся во времени.
Если в электрическое поле, которое окружает электрически заряженную частицу вещества, внесли другую заряженную частицу (пробный заряд), то последняя будет испытывать действие силы поля, причем сила поля оказывается пропорциональной величине пробного заряда и может иметь разную величину в различных точках пространства.
Напряженность электрического поля есть векторная величина, характеризующая электрическое поле и определяющая силу, действующую на заряженную частицу со стороны электрического поля.
Напряженность электрического поля есть векторная величина, равная пределу отношения вектора силы, с которой электрическое поле действует на неподвижное точечное заряженное тело, внесенное в рассматриваемую точку поля, к величине заряда этого тела, когда его заряд стремится к нулю:

Из (1.1) видно, что направление напряженности совпадает с направлением силы, действующей на положительно заряженное точечное тело.
Воспользуемся экспериментально установленной Кулоном зависимостью:

где: 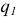 и
и 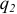 — величины точечных электрических зарядов двух тел, которые расположены в однородной изотропной среде на расстоянии
— величины точечных электрических зарядов двух тел, которые расположены в однородной изотропной среде на расстоянии 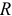 друг от друга;
друг от друга; 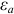 — абсолютная диэлектрическая проницаемость среды, которая связана соотношением
— абсолютная диэлектрическая проницаемость среды, которая связана соотношением 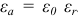 . Здесь
. Здесь 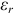 — относительная диэлектрическая проницаемость вещества, a
— относительная диэлектрическая проницаемость вещества, a 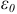 — диэлектрическая постоянная вакуума равная
— диэлектрическая постоянная вакуума равная 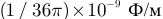 .
.
Если определить напряженность поля во всех его точках, можно провести ряд линий так, чтобы в каждой точке этих линий касательные к ним совпадали по направлению с вектором напряженности поля (рисунок 1.1).
Эти линии называют линиями напряженности электрического поля. На чертеже их изображают со стрелками, указывающими направление вектора 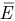 . Совокупность таких линий образует картину электрического поля. Если второй заряд
. Совокупность таких линий образует картину электрического поля. Если второй заряд 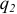 выбрать в качестве пробного и в выражение (1.1) подставить формулу (1.2), то получим:
выбрать в качестве пробного и в выражение (1.1) подставить формулу (1.2), то получим:

где 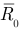 — единичный радиус-вектор.
— единичный радиус-вектор.
В соответствии с формулой (1.3) появляется физическая интерпретации вектора напряженности электрического поля как силы, численно равной силе, действующей на единичный положительный пробный заряд 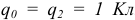 . Единицей измерения является В/м.
. Единицей измерения является В/м.
На заряд 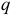 (рисунок 1.1), расположенный в произвольной точке электрического поля, действует сила:
(рисунок 1.1), расположенный в произвольной точке электрического поля, действует сила:

При переносе этого тела из точки 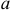 в точку
в точку 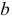 на участке
на участке 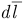 сила электрического поля выполняет работу
сила электрического поля выполняет работу 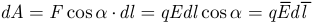 , а на всем пути от точки
, а на всем пути от точки 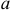 до точки
до точки 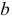 :
:
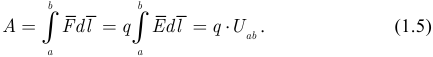
Величиной падения напряжения 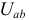 , между точкой
, между точкой 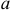 и
и 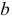 принято называть работу сил электрического поля при переносе единичного положительного электрического заряда из точки
принято называть работу сил электрического поля при переносе единичного положительного электрического заряда из точки 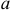 в точку
в точку 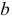 в областях не занятых источниками энергии.
в областях не занятых источниками энергии.
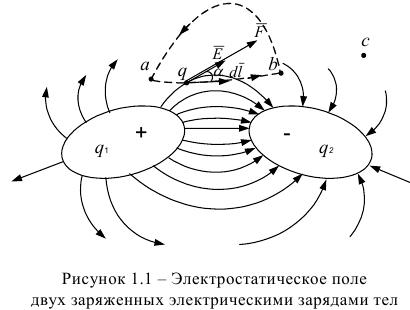
Единицей измерения напряжения является вольт (В). Если путь 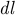 совпадает с линией напряженности поля, то
совпадает с линией напряженности поля, то 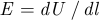 , откуда единица измерения напряженности — В/м.
, откуда единица измерения напряженности — В/м.
Если точка 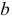 будет перемещена в точку
будет перемещена в точку 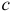 и далее в бесконечность, где нет источников поля, так как
и далее в бесконечность, где нет источников поля, так как 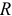 стремится к бесконечности и напряженность равна нулю, то падение напряжения
стремится к бесконечности и напряженность равна нулю, то падение напряжения 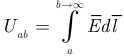 зависит только от координат точки
зависит только от координат точки 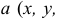
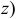 и, таким образом, является характеристикой поля в ней. Полученная скалярная величина называется электрическим потенциалом точки
и, таким образом, является характеристикой поля в ней. Полученная скалярная величина называется электрическим потенциалом точки 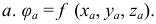
Если выбрать заряд 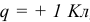 , то электрическим потенциалом точки а является работа сил электрического поля по переносу единичного положительного заряда из данной точки а в бесконечность, где нет источников поля:
, то электрическим потенциалом точки а является работа сил электрического поля по переносу единичного положительного заряда из данной точки а в бесконечность, где нет источников поля:
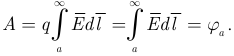
Рассмотрим разность потенциалов между точкой 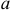 и
и 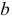 :
:
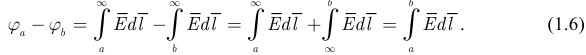
В соответствии с формулой (1.5) 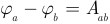 ,. Следовательно, разница потенциалов между точкой
,. Следовательно, разница потенциалов между точкой 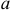 и
и 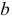 является падением напряжением между точками
является падением напряжением между точками 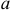 и
и 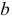 и не зависит от формы пути. Работа сил электрического поля по переносу электрического заряда по замкнутому контуру из точки
и не зависит от формы пути. Работа сил электрического поля по переносу электрического заряда по замкнутому контуру из точки 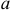 в точку
в точку 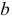 и наоборот из точки
и наоборот из точки 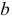 в точку
в точку 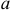 равна нулю. Действительно:
равна нулю. Действительно:
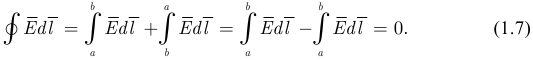
Поля, для которых выполняется равенство (1.7), принято называть потенциальными, независимо от физической природы вектора 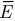 .
.
Под электрической емкостью одиночного заряда тела понимают отношение величины заряда тела к величине потенциала этого тела 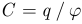 . В системе СИ емкость измеряется в фарадах
. В системе СИ емкость измеряется в фарадах 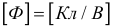 и кратных ей единицах:
и кратных ей единицах:
микрофарадах (мкФ) и пикофарадах (пФ), при этом 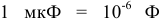 ,
, 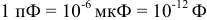
Кроме величин векторов 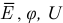 следует учитывать явление поляризации вещества:
следует учитывать явление поляризации вещества:

где: 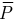 — вектор поляризованности вещества;
— вектор поляризованности вещества; 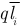 — электрический момент двух равных по значению и противоположных по знаку зарядов, находящихся на расстоянии
— электрический момент двух равных по значению и противоположных по знаку зарядов, находящихся на расстоянии 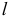 (это векторная величина, направленная от заряда —
(это векторная величина, направленная от заряда — 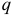 к заряду +
к заряду + 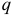 ).
).
В поляризованном веществе молекулы в электрическом отношении представляют собой диполи.
Для большинства диэлектриков вектор поляризации 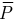 пропорционален напряженности электрического поля
пропорционален напряженности электрического поля 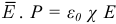 (
(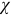 — электрическая восприимчивость).
— электрическая восприимчивость).
Интенсивность электрического поля характеризуется вектором электрической индукции или вектором электрического смещения 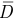 :
:
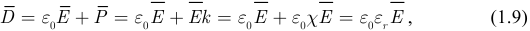
где 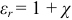 — относительная диэлектрическая проницаемость.
— относительная диэлектрическая проницаемость.
В системе СИ величины 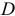 и
и 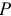 имеют одну и ту же единицу: кулон деленный на метр в квадрате
имеют одну и ту же единицу: кулон деленный на метр в квадрате 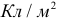 .
.
Одной из важнейших теорем электростатики является теорема Гаусса.
Поток вектора электрической индукции (электрического смещении) через любую замкнутую поверхность, окружающую некоторый объем, равен алгебраической сумме свободных зарядов, находящихся внутри этой поверхности:
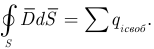
Из этой формулы следует, что вектор 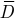 в однородных средах не зависит от диэлектрических свойств среды
в однородных средах не зависит от диэлектрических свойств среды 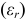 .
.
Эта страница взята со страницы задач по электротехнике:
Электротехника — решения задач и примеры выполнения заданий
Возможно эти страницы вам будут полезны:
| Проводники, диэлектрики и полупроводники |
| Электрические токи проводимости, переноса и смещения |
| Теорема компенсации |
| Линейные соотношения в линейных электрических цепях |

