В любой электрической цепи без изменения токораспределения в ней резистор может быть заменен ЭДС, числено равной падению напряжения не резисторе и направленной встречно току в этом резисторе.
Для доказательства теоремы компенсации выделим из схемы одну ветвь с резистором 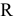 и током
и током 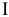 , а всю остальную часть схемы условно обозначим прямоугольником (рисунок — 3.77).
, а всю остальную часть схемы условно обозначим прямоугольником (рисунок — 3.77).
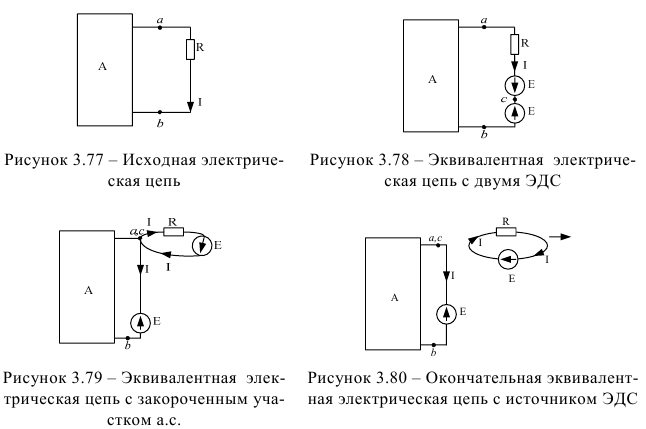
Если в выделенную ветвь включить два одинаковых и противоположно направленных источников ЭДСЕ, численно равных падению напряжения на резисторе 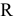 от тока
от тока 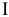 (
(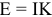 ; рисунок 3.78), то ток
; рисунок 3.78), то ток 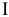 в цепи от этого не изменится.
в цепи от этого не изменится.
Убедимся, что разность потенциалов между точками а и с в схеме рисунка 3.78 при этом будет равна нулю. Действительно, 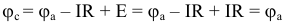 .
.
Если потенциалы точек с и а равны 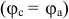 , то точки
, то точки 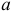 и
и 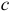 можно объединить в одну точку, то есть закоротить участок
можно объединить в одну точку, то есть закоротить участок 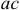 и получить схему рисунка 3.79. Режим работы электрической цепи не измениться, если замкнутый контур с элементами
и получить схему рисунка 3.79. Режим работы электрической цепи не измениться, если замкнутый контур с элементами 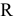 и
и 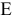 удалить. Окончательная эквивалентная цепь содержит вместо резистора ЭДС
удалить. Окончательная эквивалентная цепь содержит вместо резистора ЭДС 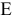 (рисунок 3.80).
(рисунок 3.80).
Эта страница взята со страницы задач по электротехнике:
Электротехника — решения задач и примеры выполнения заданий
Возможно эти страницы вам будут полезны:
