Оглавление:
Основные методы интегрирования
Метод разложения
Основан на разложении подынтегральной функции на сумму двух или нескольких функций. Применяется, если интегралы от слагаемых являются табличными или известен метод их нахождения.
Пример:
Найти неопределенный интеграл методом разложения
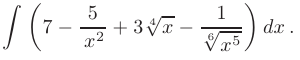
► Используя свойства неопределенного интеграла, представим исходный интеграл в виде суммы интегралов:
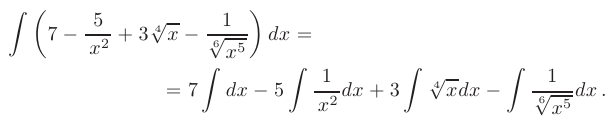
После преобразования подынтегральных функций к табличному виду получим сумму интегралов от степенных функций:
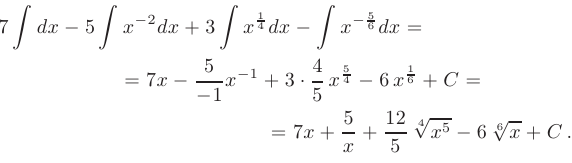
Метод замены переменной
Суть метода замены переменной или подстановки состоит в том, чтобы некоторую часть подынтегральной функции обозначить новой переменной и, используя эту новую переменную, выразить через нее все остальные части подынтегрального выражения. Данный метод позволяет существенно упростить исходный интеграл и свести его к табличному интегралу. В общем виде этот метод можно описать формулой:
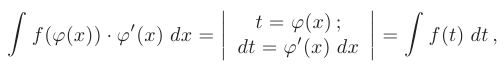
где функция 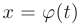 имеет непрерывную производную.
имеет непрерывную производную.
В частности, если интеграл отличается от «табличного» только аргументом подынтегральной функции, который имеет вид 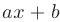 , то за новую переменную
, то за новую переменную 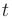 следует принять этот аргумент:
следует принять этот аргумент: 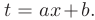 Тогда будет справедливо следующее правило:
Тогда будет справедливо следующее правило:
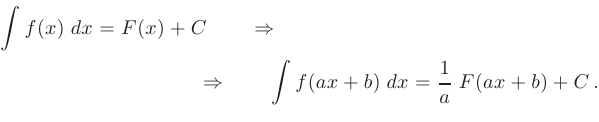
Отметим, что метод замены переменной является одним из основных методов вычисления неопределенных интегралов. Даже в тех случаях, когда мы интегрируем каким-либо другим методом, нам часто приходится в промежуточных вычислениях прибегать к замене переменной.
Пример:
Найти неопределенный интеграл методом замены переменной
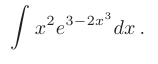
► Заметим, что множитель 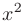 с точностью до постоянного коэффициента представляет собой производную аргумента показательной функции. Поэтому, используя замену переменной вида
с точностью до постоянного коэффициента представляет собой производную аргумента показательной функции. Поэтому, используя замену переменной вида
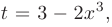
вычислим ее дифференциал

и выполним их подстановку в подынтегральное выражение:
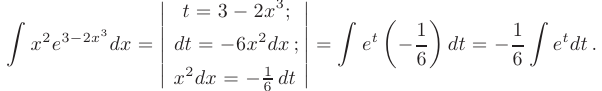
В результате замены переменной получаем табличный интеграл (см. приложение В.12). После нахождения первообразной произведем обратную замену переменной 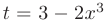 :
:
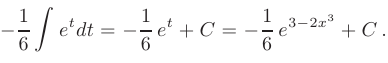
Метод интегрирования по частям
Пусть функции
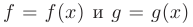
имеют непрерывные производные, тогда выражение
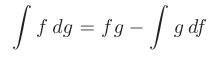
описывает формулу интегрирования по частям. Эта формула применяется, если интеграл 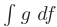 более прост для интегрирования, чем
более прост для интегрирования, чем 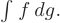 В качестве примера приведем наиболее типичные случаи:
В качестве примера приведем наиболее типичные случаи:
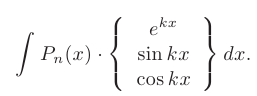
Здесь за 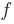 следует обозначить многочлен
следует обозначить многочлен 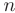 -ой степени
-ой степени 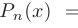
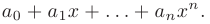
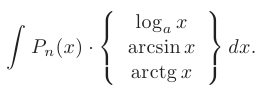
В этом случае за 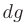 следует обозначить
следует обозначить 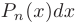 .
.
Пример:
Найти неопределенный интеграл методом интегрирования по частям
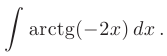
► Прежде чем приступать к интегрированию заметим, что подынтегральная функция является нечетной, следовательно, заданный интеграл можно записать в виде
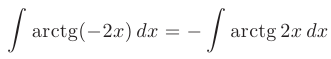
Далее в соответствии с формулой интегрирования по частям положим:
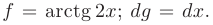
Дифференцируя функцию  и интегрируя дифференциал функции
и интегрируя дифференциал функции  получим:
получим:
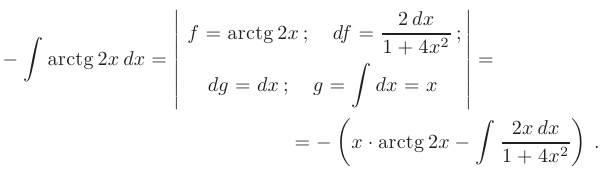
Заметим, что в последнем интеграле числитель дроби 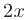 с точностью до постоянного множителя является производной знаменателя
с точностью до постоянного множителя является производной знаменателя 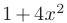 . Выполним замену переменной. Пусть
. Выполним замену переменной. Пусть 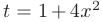 , тогда
, тогда 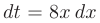 и искомый интеграл может быть записан в виде:
и искомый интеграл может быть записан в виде:
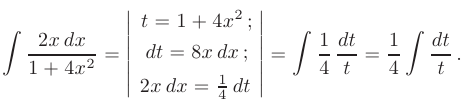
В результате получаем табличный интеграл (см. приложение В. 12), который после обратной замены примет вид:
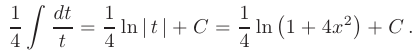
Таким образом,
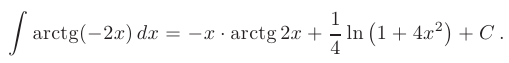
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Наибольшее и наименьшее значения функции в математике |
| Первообразная и интеграл в математике |
| Интегрирование некоторых классов функций в математике |
| Интегрирование рациональных дробей в математике |

