Основные характеристики функции
1. Функция 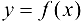 , определенная на множестве X, называется чертой, если для
, определенная на множестве X, называется чертой, если для 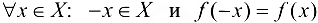 ; нечетной, если для
; нечетной, если для 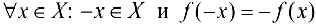 .
.
График четной функции симметричен относительно оси 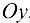 , а нечетной — относительно начала координат.
, а нечетной — относительно начала координат.
Функции не являющиеся пи четными, ни нечетными, относят к функциям общего вида.
2. Пусть функция 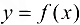 определена на множестве X и пусть
определена на множестве X и пусть 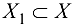 . Если для любых значений аргументов
. Если для любых значений аргументов 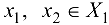 из неравенства
из неравенства 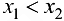 следует неравенство:
следует неравенство:
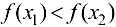 , то функция называется возрастающей на множестве
, то функция называется возрастающей на множестве 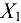
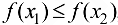 , то функция называется неубывающей на множестве
, то функция называется неубывающей на множестве 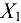 ;
;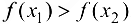 , то функция называется убывающей на множестве
, то функция называется убывающей на множестве 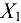 ;
; 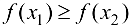 , то функция называется невозрастающей на множестве
, то функция называется невозрастающей на множестве 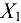 .
.
Возрастающие, невозрастающие, убывающие и неубывающие функции на множестве 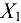 называются монотонными на этом множестве, а возрастающие и убывающие — строго монотонными.
называются монотонными на этом множестве, а возрастающие и убывающие — строго монотонными.
Интервалы, в которых функция монотонна, называются интервалами монотонности.
3. Функцию 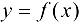 , определенную на множестве X, называют ограниченной па этом множестве, если существует такое число
, определенную на множестве X, называют ограниченной па этом множестве, если существует такое число 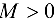 , что для всех
, что для всех 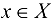 выполняется неравенство
выполняется неравенство 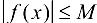 . Следовательно, график ограниченной функции лежит между прямыми
. Следовательно, график ограниченной функции лежит между прямыми 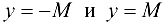 .
.
4. Функция 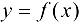 , определенная на множестве X, называется периодической на этом множестве, если существует такое число
, определенная на множестве X, называется периодической на этом множестве, если существует такое число 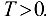 , что при каждом
, что при каждом 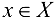 значение
значение 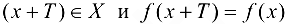 . При этом число Т называется периодом функции. Если Т — период функции, то ее периодами будут также числа
. При этом число Т называется периодом функции. Если Т — период функции, то ее периодами будут также числа 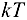 , где
, где 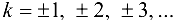 За основной период берут наименьшее положительное число Т, удовлетворяющее равенству
За основной период берут наименьшее положительное число Т, удовлетворяющее равенству
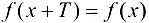
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
| Функция |
| Способы задания функций с примерами |
| Обратная функция с примерами |
| Сложная функция с примером |

