Оглавление:






Основные задачи, решаемые способом замены плоскостей проекций
- Основная цель. Решается путем изменения плоскости проекции 1. Рассмотрим четыре основные задачи. Это уменьшает решение различных проблем путем замены плоскости проекции. Первое задание Создайте прямую линию I (/) в общем положении новой системы на плоскости прямой проекции.
- Чтобы вывести эту прямую I на уровень прямой, достаточно заменить одну из плоскостей проекции, например плоскость П2, новой плоскостью П4, перпендикулярной этой плоскости, не подлежащей замене, и параллельной ей. Затем линия (/) системы (Pn P4) становится линией уровня. На прямом уровне мы знаем, что одна из проекций перпендикулярна линиям связи, поэтому эти линии связи должны быть перпендикулярны проекции.
Чтобы выполнить эту замену в сложном чертеже (рис. 88), определите новую линию связи, нарисовав новую линию связи через две произвольные точки 1 и 2 незаменимой проекции и две линии I. Людмила Фирмаль
Затем нарисуйте дно высотой G2 и L * G4, каждая вертикаль к старой 88 И новая линия связи. Кроме того, базовая плоскость Г рисуется в точке / уровне для подсчета высоты. Следовательно, высота этой точки равна / r4 = 0, поэтому новая проекция / точка 4 / является основанием Г4. Новая линия связи, проведенная через проекцию от основания G4, берется отдельно от высоты h2 точки 2, ранее измеренной в поле G12, от основания этого поля G2 для получения новой проекции. Точка 2.
После того, как проведете линию через проекцию 1K, получите новую проекцию / 4 этой линии проекции. Следовательно, линия I (горит / 4) системы плоскостей проекции (ПпП4) является прямой линией, а ее проекция / j перпендикулярна линии связи. G в L д. Легко видеть, что прямая линия / проецируется на плоскость P4 без искажений и что угол a, образованный проекцией / 4 и дном Г4, дает естественный угол наклона относительно прямой линии / плоскости Hi.
Очевидно, что рассмотренные проблемы также можно решить, заменив плоскость II! На плоскости P4, перпендикулярной P2 и параллельной прямой /. Эта замена выполняется на сложных чертежах (рис. 89). Новые линии связи здесь представляют собой неизменяемые проекции / 2 и 2r, перпендикулярно отведенные 2/2, и новые проекции / 4 и 24 построены на этих линиях связи, поэтому они относятся к базовой плоскости Φ.
Глубина точек не изменилась. Линия I проецируется на плоскость P4 без искажения, а угол, образованный проекцией / 4 и нижней F4, дает естественный угол наклона относительно линии / плоскости P2. 2. Второе задание. Новая система проекционных линейных плоскостей создает прямые линии уровня I (f Линия / — горизонтальная линия системы проекционных плоскостей (II, A2).
Замените проективную плоскость P2 новой плоскостью A4, перпендикулярной линии /. P, затем POP. Тогда система (Pt, ITJ, Линия / становится линией проекции для плоскости A На сложной диаграмме (рис. 90) новая линия связи проведена через проекцию и любые две точки 1 и 2i прямой линии. Кроме того, на этом горизонтальном уровне нарисуйте базовую плоскость Г для подсчета высоты.
В этом случае высота обеих точек 1 и 2 равна нулю. Поэтому новые проекции этих точек / 4 и 24 совпадают в одной точке в проекции Γ4 базовой плоскости G. Таким образом, мы получаем прямую / проекцию / 4 на плоскость П4 в виде точки V4 = 24/4. Если эта линия является передней, вам нужно заменить рисунок 90 на плоскость, освещенную плоскостью П4, для преобразования в проекционные линии. GG 1 час час * N Футов Рис. 89
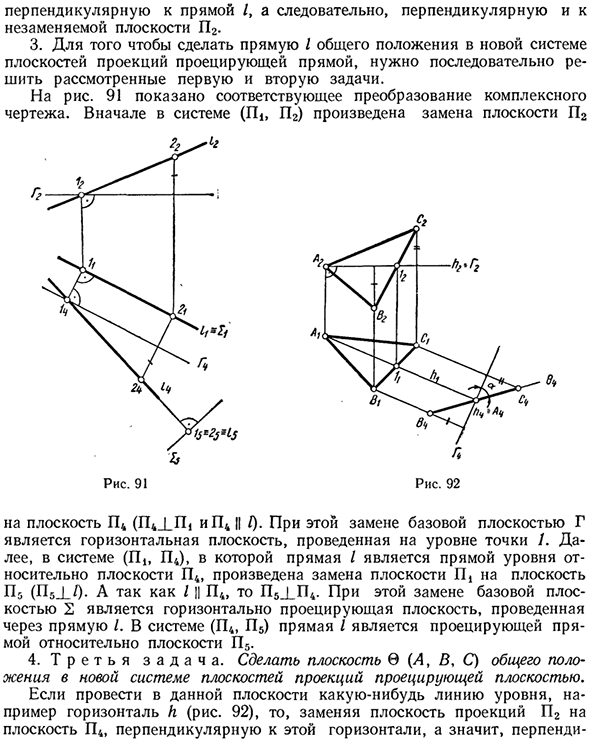
Эта строчка. б * г * 1 час Перпендикулярно прямой / и, следовательно, перпендикулярно незаменимой плоскости P2. 3. Чтобы создать прямую I в общем положении в новой системе проекционных плоскостей проекционных линий, нам необходимо решить первую и вторую задачи, рассмотренные по очереди. На рисунке 91 показано соответствующее преобразование сложного чертежа. Сначала плоскость (P2) заменяется системой (P |, P2). Рис. 91 Рис. 92 На самолет 44 (^^ ,, и41 | /).
В этой замене базовая плоскость Γ является горизонтальной плоскостью, нарисованной в точке / уровне. Кроме того, в системе (Pn P4), где линия / является линией уровня относительно плоскости P4, плоскость P заменяется плоскостью P0 (P5 ] /). А поскольку / 1 | P4, то P5 ] P4. При этой замене базовая плоскость 2 становится горизонтально выступающей плоскостью, нарисованной прямой линией /.
В системе (P4, P5) линия / — это проекционная линия для плоскости P5. 4. Третье задание. Сделайте плоскость Q (A, B, C) в общем положении новой системы в плоскости проекции плоскостью проекции. Например, рисование горизонтальной линии на этой плоскости, например горизонтальной h (рис. 92), заменяет плоскость проекции P2 этой горизонтальной плоскостью P4, и, следовательно.
- Затем для незаменимой плоскости проекции ГЦ получим горизонталь и эту плоскость, которые необходимо спроецировать на плоскость P4. Чтобы выполнить эту замену в сложном чертеже, нарисуйте новую линию связи, параллельную горизонтальной проекции hx горизонтальной h через незаменимую проекцию At, BifСt.
Поскольку линия связи является новой проекцией Аку B4 и C4, высота точек A, B и C относительно базовой плоскости G не изменяется. Поскольку точка C находится над базовой плоскостью Γ, точка B находится под ней, а их проекции C2 и B2 находятся в направлении (П2) и внешних (Пt) полей от базы Г2 соответственно, поэтому проекции C4 и Вк.
Затем нарисуйте горизонтальную плоскость Г на горизонтальном уровне h и построите ее на соответствующем новом. Людмила Фирмаль
Каждый из них также расположен от основания G4 по направлению к вам (P4) и полю пришельцев (GC) соответственно. В поле HZ проекции / C, B4 и C4 находятся на одной прямой линии, которая становится новой проекцией 94 для плоскости 0. Ссылочный угол, образованный выступ 64, имеющего основание G4 альфа дает естественный наклон по отношению к плоскости проекции HZ плоскости 0.
Аналогично, угол наклона плоскости 0 относительно плоскости P2 проекции может быть определен при выполнении замены плоскости GC. 93 Гц, перпендикулярно передней части этой плоскости Скорость 0. Четвертое задание. Сделайте плоскость проекции 0 (A, B, C) новой системы плоскостей проекции горизонтальной плоскостью. Установите плоскость 0 в горизонтальную плоскость проецирования (Рисунок 93).
Установить на уровень плоскости. Для этого замените плоскость проекции P2 плоскостью GC, параллельной этой плоскости 0. Поэтому он перпендикулярен незаменимой плоскости ГХ. В системе (GC, GC) плоскость 0 является плоскостью уровня для плоскости GC. Чтобы выполнить эту замену в сложном чертеже, нарисуйте новую линию связи через проекцию Ai Vi Ci, перпендикулярную проекции 0! Данный самолет.
Если горизонтальная плоскость Γ, нарисованная на уровне самой низкой точки C, используется в качестве базовой плоскости, высота этой точки будет равна нулю. Измерение высоты этих точек в поле P2 от основания этого поля G2 и откладывание от соответствующей базы G4 новой линии связи приведет к новым проекциям A4, £ 4 и C4 этих точек. В системе (GC, GC) плоскость 0 является плоскостью уровня для плоскости GC.
Проекция треугольника ABC Л4В4С4, определяющая плоскость 0, обеспечивает естественный вид этого треугольника. Если эта плоскость 0 является передней плоскостью проекции, то для того, чтобы сделать ее горизонтальной плоскостью, плоскость P должна быть заменена плоскостью P4, параллельной плоскости P2, и, следовательно, перпендикулярной плоскости P2. 6.
Чтобы сделать плоскость 0 (ABC) общей позицией в новой системе проекционных плоскостей с плоскостями уровней, необходимо решить проблемы, рассмотренные на третьем и четвертом этапах. На рисунке 94 показано соответствующее преобразование для сложного чертежа. Сначала в системе (ПпП2) плоскость П2 была заменена плоскостью П4, перпендикулярной горизонтали h плоскости 0. Итак, П4_1_П и П4_1_0.
При этой замене базовая плоскость становится горизонтальной плоскостью Г, нарисованной на горизонтальном уровне L. Затем в системе, где плоскость 0 является плоскостью проекции для плоскости П4 (ПпП4), плоскость П заменяется (плоскость П51 | 0, то есть П5_1_П4, при этой замене базовая плоскость 2 рисуется через точку С Горизонтально спроецированная плоскость, в системе (P4, P:.) Плоскость 0 является плоскостью уровня для рисунка 94.
Плоскость P5 и, следовательно, проекция AbBbC $ треугольника ABC обеспечивает естественный вид этого треугольника. 7. Рассмотрим несколько примеров. Решение ограничено этими четырьмя основными задачами. Пример 1. Из точки A опустите нормаль к прямой линии / общему положению (Рисунок 95).
Замена плоскости A2 на плоскость A4II / (см. Первую основную проблему) для создания прямой линии на этом уровне будет поддерживать нормальность уровня прямой во время этого изменения в поле P4, поэтому желаемая вертикальная линия Легко рисовать. Поэтому нижняя точка A от новой проекции Ai перпендикулярна линии / проекции / 4, 95 Получите желаемую перпендикулярную проекцию АкВк.
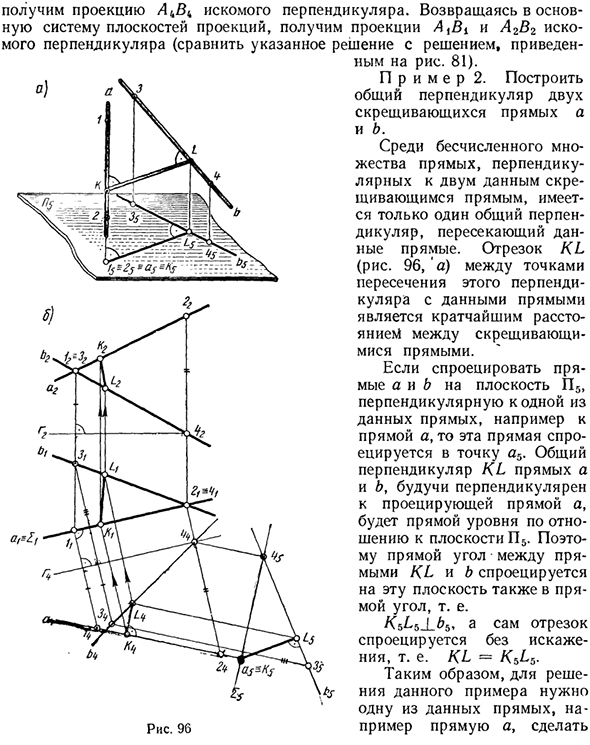
Вернитесь в основную систему на плоскости проекции и получите нужные перпендикулярные проекции AxBi и A2B2 (сравните это решение с решением, показанным на рисунке 81). ^, Пример 2. Сборка Общий перпендикуляр двух пересекающихся линий а и б. Из множества прямых линий, перпендикулярных двум заданным линиям пересечения, существует только один общий перпендикуляр, который пересекает эти линии.
Отрезок KL (рис. 96, а) между пересечением этого перпендикуляра и этих линий является кратчайшим расстоянием между пересечениями. Если вы проецируете линии a и b на одну из этих линий, например плоскость A5, перпендикулярную линии a, эта линия проецируется на точку a. Общая вертикаль KL линий a и b, перпендикулярных линии проекции a, представляет собой линию, параллельную плоскости A5.
Следовательно, прямой угол между линиями KL и L также проецируется на эту плоскость под прямым углом. Сам сегмент проецируется без искажений. Другими словами, KL-Ki> L5. Поэтому, чтобы решить этот пример, вам нужна одна из этих линий на рисунке 1. 96 примеров прямо, сделай Проекционная линия (см. Первую и вторую основные задачи).
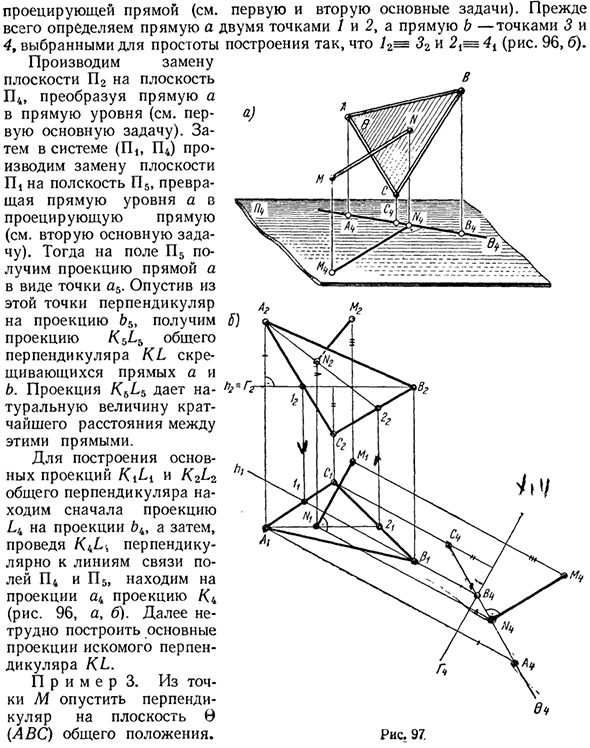
Сначала определите линию a с двумя точками / и 2, и определите линию b с точками 3 и 4Y, чтобы упростить конфигурацию так, чтобы 32r 32 и 2 = 4i (рис. 96, b). Замените плоскость P2 плоскостью P4 и преобразуйте линию a в линию уровня (см. Первую серьезную проблему). Затем в системе (P, P4) замените плоскость nt плоскостью P5 и преобразуйте уровень линия в спроецированную линию (см. Вторую основную проблему).
Далее получаем проекцию прямой a в виде точки a5 в поле P1. Если мы пропустим перпендикуляр от этой точки до проекции, мы получим проекцию K’X3 общего перпендикуляра KL пересекающихся линий a и b. Проекция KLZ дает естественное значение кратчайшего расстояния между этими линиями. Чтобы построить общие перпендикулярные главные проекции K \ LX и / (2L2), сначала найдите проекцию L4 в проекции 64, а затем нарисуйте перпендикулярную.
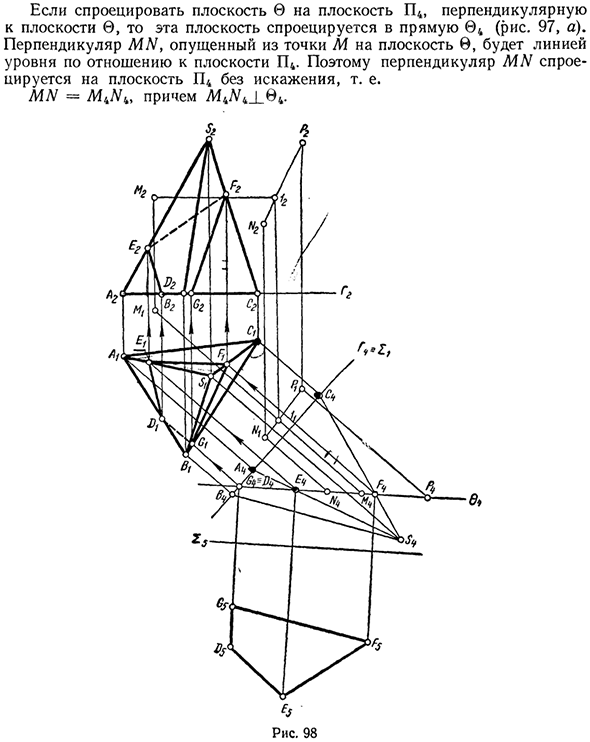
Помимо линий связи в полях P4 и P5, есть проекция K4 в проекции a4 (рис. 96, a, b). Кроме того, легко создать желаемую вертикальную главную проекцию KL. Пример 3 Опускание перпендикуляра из точки M в плоскость B {ABC) Генерал. Рисунок 97. При проецировании плоскости 0 на плоскость P4, перпендикулярную плоскости 0, эта плоскость проецируется на линию 04.
Рис. 97, вертикальная точка MN, опущенная из точки M в плоскость 9, становится горизонтальной линией относительно плоскости P4. Следовательно, вертикальная MN представляет собой плоскость P4 без искажений, то есть MN = и Af4N4_L04. Рисунок 98 Следовательно, для решения этого примера плоскость 6 должна быть плоскостью проекции (см. Третью основную задачу).
Замените плоскость P2 плоскостью P4 и сделайте плоскость 0 плоскостью проекции (рис. 97, б). Далее получаем проекцию плоскости 0 в виде линии 04 в поле P4. После падения перпендикуляра от проекции LC к проекции 04, получите проекцию M4jV4 требуемого вертикального MN. Проекция M4 LC дает свой натуральный размер.
Чтобы построить основной прогноз ASCC и M2N2 до желаемой нормы, LCC выполняется перпендикулярно линиям связи в полях GC и P4. Проекция N2 основания N перпендикуляра получается из условия, при котором поддерживается высота точки N при замене плоскости G12 на G14. Чтобы контролировать точность построения проекций LC и N2, убедитесь, что точка N принадлежит плоскости 0.
Пример 4. Создание спроецированного и естественного вида разреза плоскости SABC 0 (M, N, P) пирамиды в общем месте (рис. 98). Вместо замены плоскости проекции можно построить проекцию нужного сечения, определив вершины сечения как пересечение ребер пирамиды и конкретной плоскости в общем месте.
Однако, в дополнение к проекции разреза, вам также необходимо создать естественный вид разреза. Для этого сначала сделайте эту плоскость плоскостью проекции (см. Третью основную проблему), а затем горизонтальной плоскостью (см. Четвертую основную проблему). Это облегчает создание проекции поперечного сечения после преобразования второй плоскости в плоскость проекции.
Решением в этом примере является последовательное применение третьей и четвертой основных задач. Замените плоскость проекции P2 плоскостью P4, перпендикулярной горизонтальной плоскости h плоскости 0, и преобразуйте эту плоскость в плоскость проекции. В то же время спроецируйте на эту плоскость P4 и эту пирамиду. Далее в поле П4 можно легко создать проекцию сечения D4 £ 4 / r4G4.
Отметьте пересечение проекции 04 и проекции края пирамиды. Вернуться в основную систему, проекция {Gi и D2E2F2G2 Желаемый раздел. Затем в системе (P, P4) замените плоскость GZ плоскостью GZ, параллельной плоскости 0, и сделайте эту плоскость горизонтальной плоскостью. Затем естественная форма DbEbFbGb целевого поперечного сечения приобретается в поле ГЦ.
Смотрите также:
Примеры решения задач по начертательной геометрии
| О преобразовании комплексного чертежа | Способ вращения вокруг проецирующей прямой |
| Основы способа замены плоскостей проекцией | Способ вращения вокруг прямой уровня (способ совмещения) |

