Основные понятия статистической гидромеханики

Основные понятия статистической гидромеханики

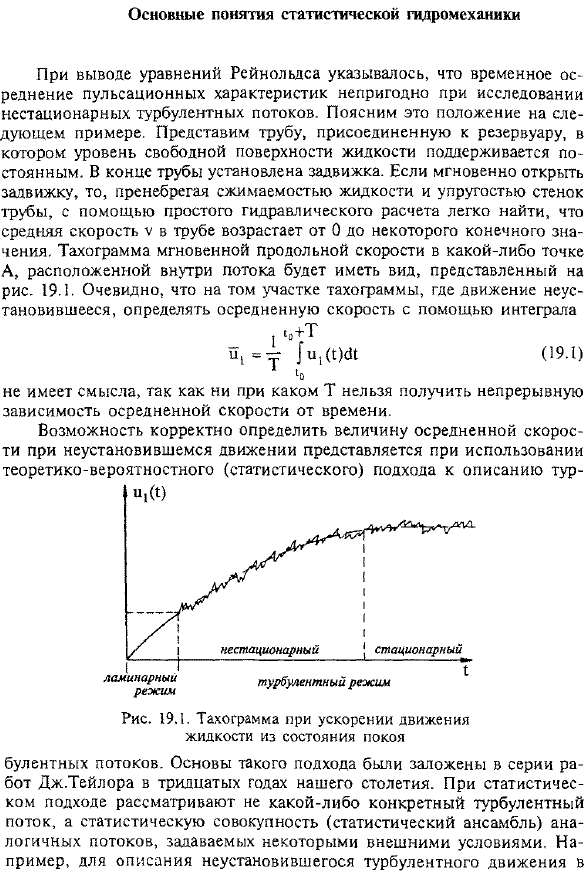
Основные понятия статистической гидромеханики. При выводе уравнения Рейнольдса было указано, что усреднение по времени характеристик пульсаций нецелесообразно для исследования нестационарной турбулентности. Следующий пример иллюстрирует это положение. Представьте себе трубу, прикрепленную к резервуару, где уровень свободной поверхности жидкости поддерживается постоянным. Клапан прикреплен к концу трубы. Используя простой гидравлический калькулятор, вы можете легко увидеть, что средняя скорость V трубы увеличивается от 0 до определенного конечного значения, если вы открываете клапан мгновенно, игнорируя скорость сжатия жидкости и эластичность стенок трубы. Мгновенная тахограмма вертикальной скорости в любой точке а внутри потока принимает вид, показанный на рисунке 3. 19.1.

Очевидно, что в том участке тахограммы, где движение неустойчиво, определяют среднюю скорость с помощью интеграла. Людмила Фирмаль

• Это не имеет смысла, так как невозможно непрерывно получать временную зависимость средней скорости в любом т. Возможность точного определения величины средней скорости при нестационарном движении объясняется с помощью вероятностного (статистического) подхода. Кипятить струю. Основой такого подхода стали 30-е годы нашего века J. It был поставлен в серии работ Тейлора. При статистическом подходе учитывается не конкретная турбулентность, а статистический ансамбль (статистический ансамбль) аналогичных потоков, заданных в определенных внешних условиях. Например, чтобы объяснить установившуюся турбулентность в трубе 352, где клапан открывается мгновенно, вы должны открыть клапан много раз (s раз) и исследовать весь поток (полученный из каждого отверстия).

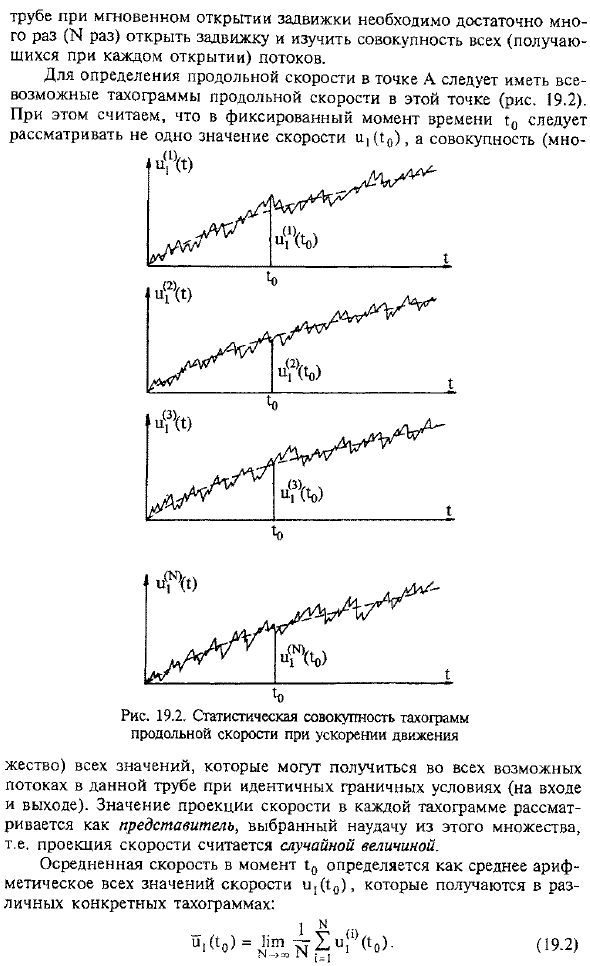
Чтобы определить продольную скорость точки А, нужны всевозможные тахограммы продольной скорости в этом отношении(рис. 19.2).кроме того, в определенной точке Е0, вместо 1 значения скорости IDE0, устанавливают（ г Значение проекции скорости каждой такограммы всех возможных значений, которые могут быть получены во всех возможных потоках в конкретной трубе при одинаковых граничных условиях (входных и выходных), считается случайным образом выбранным представителем из этого множества. Проекция скорости считается случайной величиной. Средняя скорость во времени T0 определяется как среднее арифметическое всех значений скорости ID1 (0), которое получается на различных конкретных тахограммах. Статистический подход позволяет использовать математический аппарат теории вероятностей, установленный при описании турбулентности flows.

• Например, при использовании соответствующей теоремы теории вероятностей для определения процедуры усреднения свойств турбулентности по правило усреднения Рейнольдса выполняется автоматически. Статистический подход к описанию турбулентности также используется для стационарных motion. In в этом случае возникает вопрос, совпадает ли средняя скорость, определяемая по среднему времени(по зависимости (19.1)), со средней скоростью, вычисленной по среднему статистическому ансамблю(по зависимости (19.2)).Доказательством равенства этих средних величин является содержание так называемой теоремы сергодича. Если это уравнение вводится как предположение, то оно называется эргодической гипотезой.

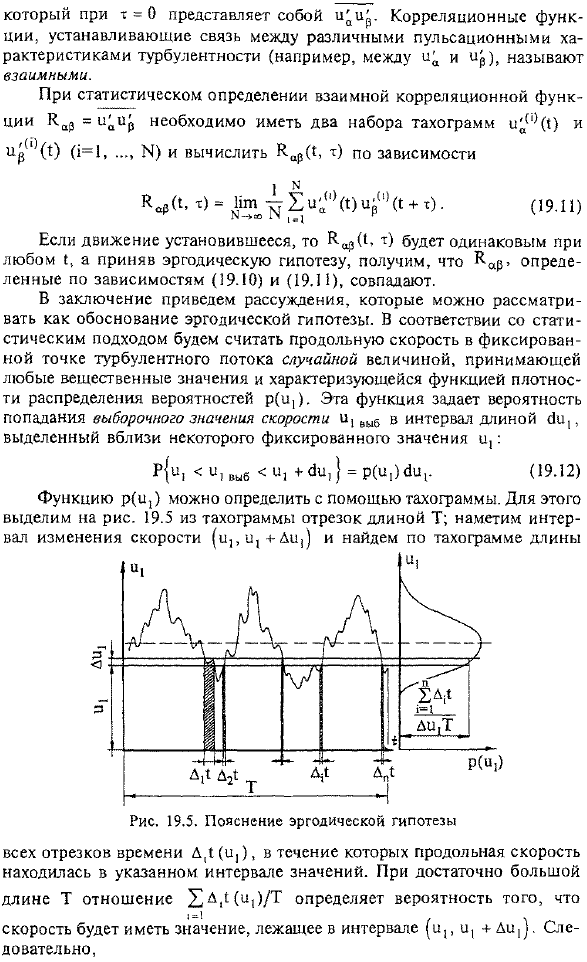
В стационарных граничных условиях(например, при фиксированном открытии клапана в трубе) можно получить такограмму любой длины (за любой длительный промежуток времени).Разрезать такую такограмму на большое количество фрагментов, достаточно длинных(это означает «достаточно длинный фрагмент».Это будет разъяснено из следующего описания).Если рассматривать каждый фрагмент как отдельную такограмму, а совокупность полученных тахограмм считать статистической совокупностью (ансамблем), то средняя скорость P1 (T) определяется по формуле для каждого момента (19.2). Эргодическая гипотеза считается справедливой. Отныне средняя скорость во всех точках будет одинаковой, то есть.

Перед рассмотрением взаимности различных методов усреднения приведем несколько методик статистической обработки тахограмм со стабильными турбулентными движениями. Людмила Фирмаль

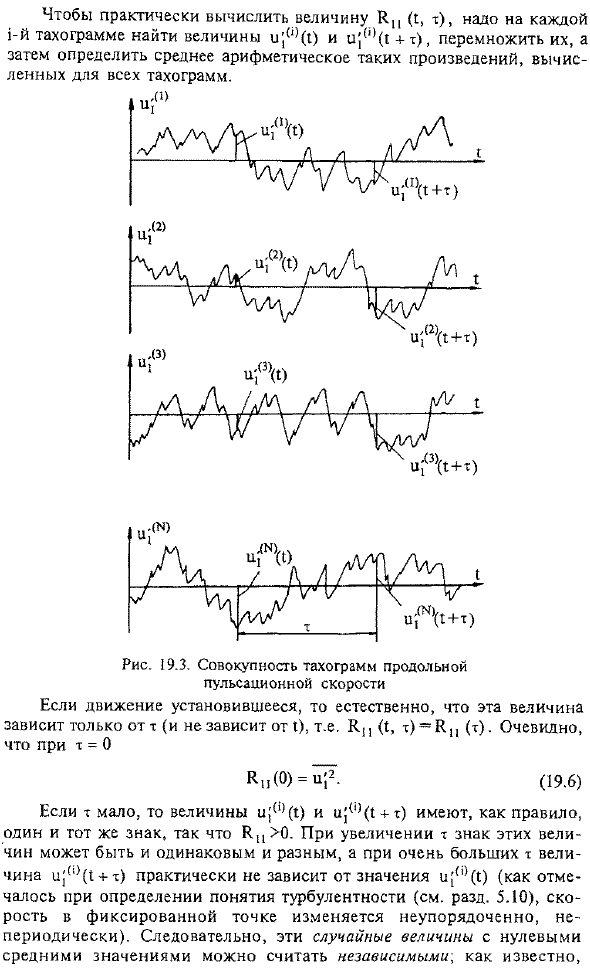
• Вычитание 1С из всех значений мгновенной скорости и[1}(1) создает тахограмму с продольной пульсирующей скоростью u^.это показано на рисунке. Скорость и.{Набор октограмм против 1 из проекций. Аналогичный набор тахограмм может быть построен против 2 других проекций пульсирующей скорости u и C. Определение временной корреляционной функции (или автокорреляционной функции) продольной пульсирующей скорости K имеет вид: Чтобы реально вычислить значение Hn(I, m), нужно найти в каждой 1-й такограмме величины u ^(1) и u ^(1; + m), умножить их и определить среднее арифметическое такого произведения, рассчитанное для всех тахограмм.

Смотрите также:

Примеры решения задач по гидравлике

Возможно эти страницы вам будут полезны:

1. Потери напора по длине в круглой трубе.
2. Полуэмпирические методы решения задач о свободной турбулентности.
3. Частотные характеристики турбулентности.
4. Задачи экспериментального изучения движения жидкостей.