Основные понятия кинематики и динамики жидкости.

Основные понятия кинематики и динамики жидкости.

Основные понятия кинематики и динамики жидкости. Скорость жидкой частицы зависит от координат x, y, z и времени t этой частицы. Плотностьи давление P также являются функциями координат и времени =(х, у, Z, т); р = р(х, у, Z, Т). Если характеристики потока не зависят от времени, то есть их можно изменять только от точки к точке, то поток называют стабильным. Если в определенной точке пространства характеристики потока изменяются со временем, то поток называется нестационарным. Линия потока-это линия в каждой точке, где вектор скорости касается этой линии. Форма уравнения линии потока имеет вид (2.1） Где uy, uz-компоненты вектора скорости. Серия линий тока, проходящих через замкнутый контур L, образует трубчатую поверхность или трубку тока. Жидкость в текущей трубке образует струйку.

Если контур L является небольшой, текущая пробка и поток, называются элементарными. Обычное сечение струйки в каждой точке каждой линии тока называется живым сечением. Людмила Фирмаль

• Область конечномерного пространства, занимаемая движущейся жидкостью, называется потоком. Поток обычно рассматривается как совокупность элементарных потоков. Живое сечение потока определяется таким же образом, как и в случае основного потока. Гидравлический радиус живого участка Rg это отношение площади живого участка s к влажному периметру. РГ = с /. (2.2） Влажная граница понимается как часть геометрического биосовместимого участка, где жидкость находится в контакте с твердой стенкой. Если форма и площадь живого сечения по длине потока не изменяются, то поток называют равномерным. В противном случае поток называется неравномерным. Если длина живой части изменяется плавно, то поток называется плавно меняющимся.

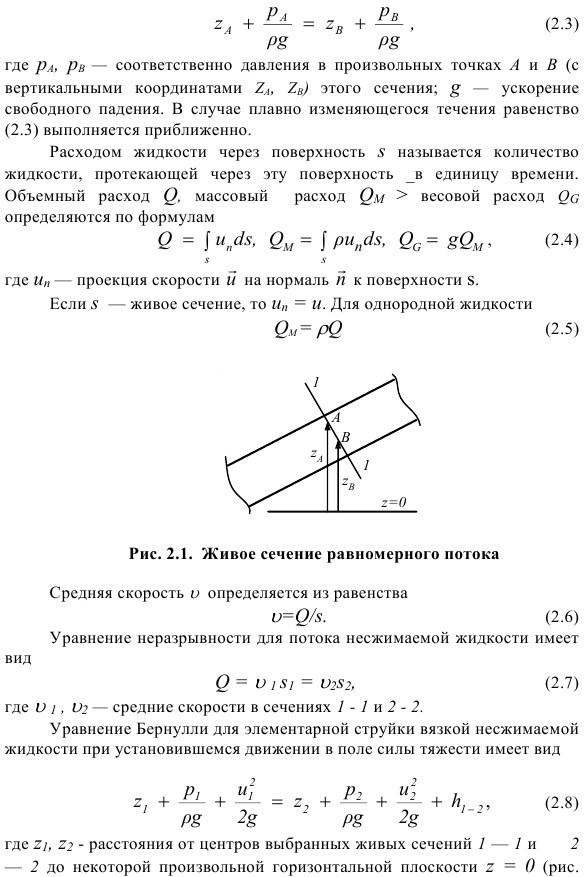
• В Живом сечении 1-1 однородного потока (рис.2.1) выполняется закон распределения гидростатического давления. (2.3） Где pA, pB-давление в любой точке A и B (вертикальные координаты ZA, ZB) в этом сечении соответственно. g-ускорение свободного падения; для плавно меняющихся течений уравнение (2.3) почти заполнено. Поток жидкости через поверхность s это количество жидкости, протекающей через эту поверхность в единицу времени. Объемный расход Q, массовый расход QM>массовый расход QG определяется по формуле (2.4） Где n-проекция скорости на Нормаль поверхности s. если S представляет собой прямую секцию, затем ООН = у. Для однородной жидкости КВ. М =М (2.5） Рисунок 2.1.Равномерный поток живого сечения Средняя скоростьопределяется из уравнения = М / С. (2.6） Уравнение неразрывности для течения несжимаемой жидкости принимает вид М =1 С1 =2s2 (2.7） Где1,2-Средняя скорость участков 1-1 и 2-2. Основное уравнение струйки Бернулли вязкой несжимаемой жидкости, которая устойчиво движется в гравитационном поле、 (2.8） Где z1, z2-расстояние от центра выбранного биометрического участка 1-1 и 2-2 до любой горизонтальной плоскости z = 0(рис. 2.2). 1,2-скорость; P1, P2-давление этих секций. h1-2-потеря давления в области между выбранными участками.

Уравнение Бернулли представляет собой закон сохранения механической энергии. Значение (2.9） Она называется полным давлением и представляет собой удельную (на единицу силы тяжести) механическую энергию жидкости в рассматриваемом сечении. Людмила Фирмаль

• z-это геометрическое давление или положение определенной потенциальной энергии. п /(г) пьезоэлектрический головной или конкретных потенциальных энергию давления; У2 /(2г) скорость головки или определенной кинетической энергии. Н1-2-часть удельной механической энергии, затрачиваемой на работу силы трения в области между перепадами давления, т. е. сечением 1-1 и сечением 2-2 (см. рис. 2.2). Для идеальной жидкости h1-2 = 0. Для плавно меняющегося течения с установившимся движением вязкой несжимаемой жидкости в гравитационном поле уравнение Бернулли имеет вид: (2.10)） Где p1-давление в случайно полученных точках на участках 1-1 и 2-2 координат z1 и Z2 соответственно (обычно получаются точки на оси потока). 1,2-Средняя скорость этих участков. А1, А2-коэффициент Кориолиса, учитывающий неравномерное распределение скорости движения частиц жидкости в разрезе. При протекании через круговую цилиндрическую трубу обычно используется= 2 в режиме ламинарного течения и � � 1.1 в турбулентном потоке-при решении практических задач обычно используется = 1. Следует отметить, что при использовании уравнения Бернулли (2.8) или (2.10) число поперечных сечений увеличивается в направлении движения жидкости flow. As вычисленный, выберите участок (ручеек), где известны величины 1,2 (u1, u2) и p1, p2. Самолет.

Смотрите также:

Примеры решения задач по гидравлике

Возможно эти страницы вам будут полезны:

1. Прямолинейное равноускоренное движение сосуда.
2. Равномерное вращение сосуда вокруг вертикальной оси.
3. Режимы движения жидкости и основы гидродинамического подобия.
4. Основные законы движения газа.