Оглавление:






Основные положения анализа размерности. П-теорема
Основные положения анализа размерности. П-теорема. Основой размерного анализа является положение о том, что все математические уравнения, представляющие связь между физическими величинами(параметрами потока жидкости или газа в гидродинамике), должны быть размерно однородными или размерно однородными. Это означает, что. Размеры в правой части уравнения должны совпадать с размерами в левой части того же уравнения. Только величины одного измерения могут быть добавлены и вычтены. С помощью этих очевидных правил (вряд ли кто-то может прибавить 1 кг на 1 метр) можно получить нетривиальный результат.
С одной стороны, результат получается»как из ничего»из бесспорного допущения, не сходного с обычными основаниями физической науки. С другой стороны, результат не имеет окончательной формы физической зависимости и требует дополнительного, в большинстве случаев экспериментального изучения явления. Людмила Фирмаль
- Приведем пример основных особенностей методики, используемой для размерного анализа, а также возможностей, которые она предоставляет. Во-первых, мы исправляем, что в динамике жидкостей и газов используются первичные размеры. Масса M; длина B; время t, температура 0 В дальнейшем с помощью размерного анализа будет рассматриваться только изотермическая задача, а температура не будет входить в размерные параметры, определяющие интересующий нас гидродинамический феномен.
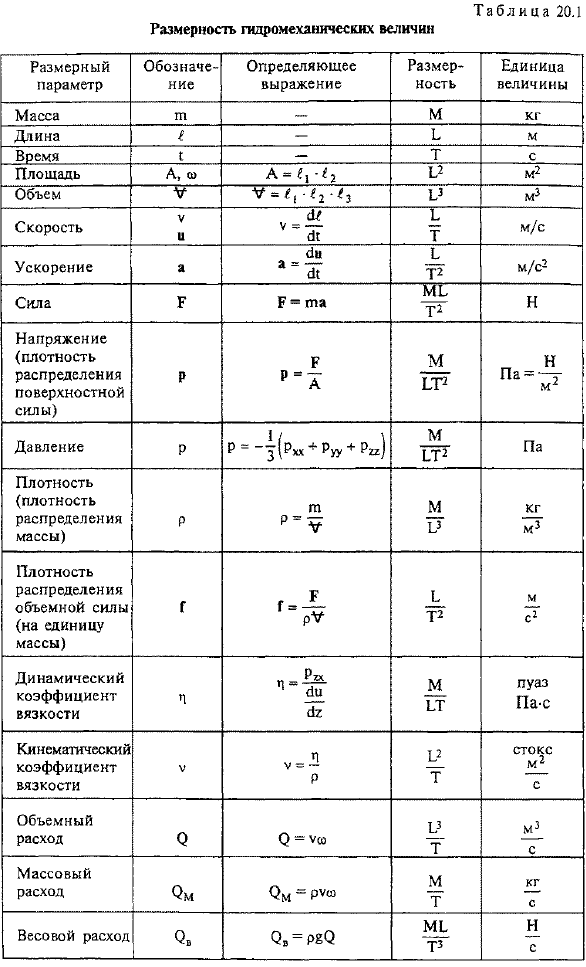
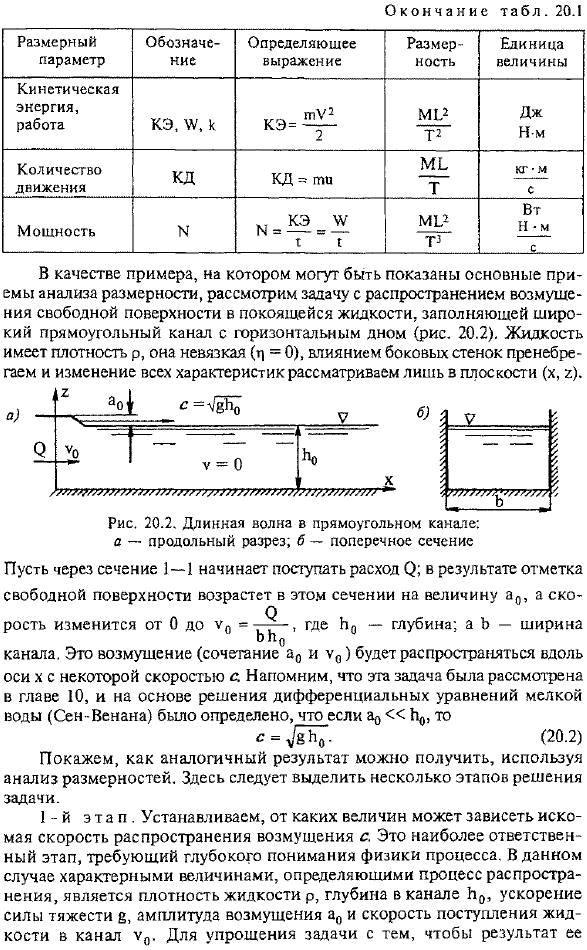
Поэтому мы предполагаем, что существует 3 отдельных первичных измерения. M, b, T. размеры других физических параметров называются вторым порядком или дифференциальными.В таблице приведены размеры (параметры размеров) величин, наиболее часто используемых в гидродинамике. 20.1. В качестве примера, демонстрирующего основной метод размерного анализа, рассмотрим задачу о распространении возмущения свободной поверхности жидкости в стационарном состоянии, которая встречается в широком прямоугольном канале с горизонтальным дном (рис. 20.2).Плотность жидкости равна P, невязка (n-0), пренебрегая действием боковых стенок и учитывая изменение всех свойств только в (x, d) plane.
- В результате в этом разделе метка свободной поверхности увеличивается до a0, а скорость изменяется от 0 до Y0= -.Где B0-глубина. b-ширина Канал. Это возмущение (комбинация a0 и V0) распространяется вдоль оси x с определенной скоростью a. эта задача рассматривается в главе 10, основанной на решении дифференциальных уравнений мелкой воды (Сен-Венана), а затем Демонстрирует, как использовать анализ размеров для получения аналогичных результатов. Здесь необходимо выделить несколько этапов решения проблемы. Первая ступень. Установите, от чего зависит искомая скорость распространения возмущения s. Это самый важный этап, который требует глубокого понимания физики Земли. process.
In в этом случае особенностью, определяющей процесс распространения, является плотность жидкости p, глубина канала b0, ускорение свободного падения e, амплитуда возмущения a0 и скорость притока жидкости в канал V0.To упростите задачу так, чтобы результат этого решения можно было сравнить с (20.2), используйте гл. 10, » Н0 и У0с, так что эти значения не влияют на процесс (принятие таких допущений является обязанностью первого этапа). в то же время Этап 2. Заменяет размеры для всех величин (20.4) и требует, чтобы размеры слева были равны размерам справа. Если приравнять экспоненты одноименной размерности, то получим систему уравнений 3-й этап. +
Они являются производными от зависимостей, которые определяют эти параметры. Людмила Фирмаль
- Если вы решите эту систему、 В результате выражение (20.2) принимает вид: Обратите внимание, что если вы сравниваете (20.5) и(20.2), то, анализируя размеры, вы получаете зависимую структуру c из§и b0.Это то же самое, что использовать дифференциальные уравнения мелководья. Однако для расчета скорости С по формуле (20.5) необходимо определить величину безразмерного коэффициента К. Поскольку анализа этой размерности недостаточно, необходимо провести эксперименты или использовать дифференциальные уравнения движения жидкости. размеры всех величин, от которых зависит величина с, различны.
Согласно утверждению об однородности размеров, их нельзя суммировать, следовательно, можно достичь одинаковых размеров только с левой и правой стороны (20.2), подняв эти величины (p, b0 и§) до определенной степени и составив из них продукты. С точки зрения размерности, 1 глубина b0 достаточно, чтобы сделать 1 эксперимент в 1 лотке, и значение k, увиденное в этом эксперименте, может быть использовано во всех других глубинах. Кроме того, анализ размеров показывает, что скорость с не зависит от типа жидкости, то есть как от воды, так и от ртути.
Смотрите также:
Примеры решения задач по гидравлике
Возможно эти страницы вам будут полезны:

