Основное уравнение равномерного движения жидкости

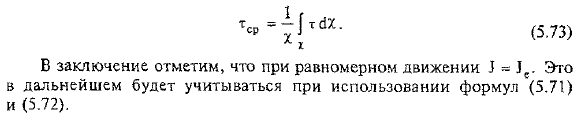
Основное уравнение равномерного движения жидкости

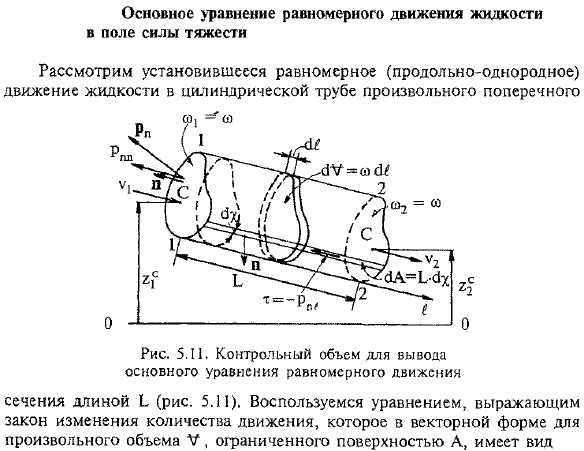
Основное уравнение равномерного движения жидкости. Рассмотрим устойчивое, равномерное (продольно равномерное) движение жидкости в произвольной поперечной цилиндрической трубе Длина секции b (рис. 5.11).Используйте уравнения, представляющие законы изменения импульса. Это векторная форма любого объема V, заключенного в поверхность A、 Проекция членов этого уравнения на ось совпадает с направлением скорости жидкости. Где; проекция вектора скорости на ось C, очевидно, и= И = |и|; проекция вектора плотности распределения внешних объемных сил на ось B I. определить напряжения pn/, принимая во внимание N ca1 в противоположном направлении от 1U a и u в том же направлении (и принимая во внимание раздел 5.1 леммы 1).

Если сторона потока представляет собой неподвижную твердую поверхность, то знак минус вводится таким образом, чтобы касательное напряжение m было положительным. Людмила Фирмаль

• В этом случае pn /-тангенциальное напряжение, действующее со стороны Abok (перпендикулярно этой поверхности n) и ориентированное вдоль оси (pn и pn-нормальные напряжения поверхности сечение O и ω соответственно).в результате это выглядит так: Внутрь!»: РП= РПП = ПП на СО2 ’■Пн; = + Р»= » П2; А6 (Вт: РШ-напряжение сдвига. Поскольку движение является устойчивым, локальная составляющая реальной производной равна нулю, а при равномерном (продольно равномерном) движении плотность распределения импульса ri вдоль потока не изменяется, и, следовательно, конвективная составляющая реальной производной также равна нулю. (5.61) результат перепишите в следующий формат.

• Гравитационный потенциал I)= & 2, следовательно, Г,=&гас1 {и = = −2-、 Объемный элемент (IV, предполагая, что стороны цилиндрические) называется (IV-oh?。 Где 2 [и 2-вертикальные координаты 2 произвольных соответствующих (на одной линии потока) точек сечения co и co2. Согласно Лемме 2 (см. раздел 5.1) и зависимости гидростатического давления от плоскости (2.33), последние 2 интеграла из (5.62) представляются в следующем виде: Где P3 и p? Это центр тяжести и давление w2. Перейдем к интеграционным соображениям на стороне аббока. Для простоты укажите напряжение сдвига pn ^ = M. Поскольку движения равномерны, можно взять полосу 1lZX в качестве элемента B. где b-длина выделенного управляющего объема, а 6X-основная длина смачиваемого участка (см. рис. 5.11).

Форма интеграла в этом случае имеет вид (5.63) если вы подставляете (5.65) в исходное уравнение (5.62)、 поскольку bx и r2 соответствуют любым соответствующим точкам в разделах 1-1 и 2-2, мы предполагаем, что это вертикальные координаты центроида разделов 1-1 и 2-2.Если разделить все члены уравнения (5.66) на p&W. Если движение в разрезе равномерное, как описано выше、 Где H-потенциальное давление. Имея это в виду, он представляет(5.67) в виде: Где I-пьезоэлектрическое смещение. Это общий вид основных уравнений равномерного движения.

Более широко эта формула используется в некоторых случаях, когда m является постоянным во всех точках вокруг увлажненной области. Людмила Фирмаль

• Это условие выполняется точно в цилиндрической форме и почти точно в прямоугольных каналах, которые очень широки. Уравнение(5.69) преобразуется в следующий вид Уравнения (5.71) и (5.72) используются не только для описанных выше случаев, но и для каналов с различными формами поперечного сечения, вводя в эти уравнения среднее касательное касательное напряжение вместо X. В заключение отметим, что при равномерном движении она равна 3 = 1e. при использовании формул (571) и (572) это учитывается далее.

Смотрите также:

Примеры решения задач по гидравлике

Возможно эти страницы вам будут полезны:

1. Геометрическая и энергетическая интерпретации слагаемых, входящих в уравнение Бернулли.
2. Потенциальный и полный (гидродинамический) напоры. Пьезометрическая и напорная линии.
3. Два режима движения жидкости.
4. Потери напора при установившемся равномерном движении жидкости (потери по длине).