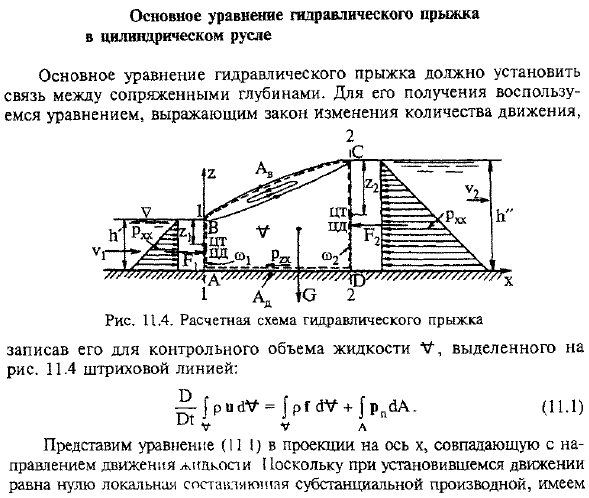
Основное уравнение гидравлического прыжка в цилиндрическом русле. To достаньте его, используйте уравнение, представляющее закон изменения импульса. Запишите его для контроля объема жидкости U1 11.4 пунктирной линией： Он представляет собой уравнение (II 1) в проекции на ось x, совпадающее с направлением движения оси и(1) равно нулю в установившемся движении, поэтому локальная составляющая существенной производной равна нулю.
Основное уравнение гидравлического скачка заключается в установлении соотношения между сопряженными глубинами. Людмила Фирмаль
- Контролируемая поверхность а, являющаяся границей объема «V», состоит из поверхностей а> 1 и©2(поперечные сечения транспортной струи 1-1 и 2-2, имевшие дно А1), А АВ-поверхность ролика ВС. Очевидно, что граничная поверхность H и текущая поверхность Ai, нормальная составляющая скорости un равна 0.Проекции на поверхность©и на оси поверхности©и © 2 x задаются только напряжением P^, нормальным к этим поверхностям, и касательным напряжением pa на поверхности Ad. Сделать 3 предположения. 1.Движения секций 1-1 и 2-2 плавно изменяются. Затем, согласно второму. 5.1 (Лемма 1) принято.
- Кроме того, это предположение позволяет предположить, что гидродинамическое давление в секциях 1-1 и 2-2 распределяется по законам гидростатического давления(см. раздел 5.1, Лемма 2). Где 2, I22-расстояние от свободной поверхности до центра тяжести в разделах 1-1 и 2-2 (см. раздел 2.4 (2.33)). 2.Поскольку касательное напряжение pa очень мало, вклад в уравнение (11.3) пренебрежимо мал. 3.It можно предположить, что продольный наклон дна пласта невелик, а проекция ускорения силы тяжести на ось Х незначительна. ？х = 0. Учитывая вышесказанное, перепишите выражение (11.3) в следующий вид.
На поверхности взаимодействие воздуха и жидкости игнорируется, поэтому напряжение также равно нулю. Людмила Фирмаль
- Используя коэффициент Буссинеска a0(см. раздел 5.2 (5.15)), запишите формулу (11.5) в следующем виде: если вы уменьшите с помощью p§и введете расход 0 = V ^ = V2 * b, вы получите основное уравнение гидравлического скачка. Свойство определения функции прыжка заключается в том, что она принимает то же значение, что и значение сопряженной глубины, и»присваивает ему».Минимальное значение этой функции аналогично функции K =(()), эти 2 функции часто строятся на одном графике (рис.11.5), и вы можете использовать функцию перехода для определения глубины сопряжения и использования потерь энергии в прыжке. Вызовите E (1g) для вычисления.
Смотрите также:
Примеры решения задач по гидравлике
Возможно эти страницы вам будут полезны:
- Классификация длинных волн в каналах.
- Общее описание гидравлического прыжка.
- Основное уравнение гидравлического прыжка и его длина в прямоугольном русле.
- Местоположение гидравлического прыжка в канале
