Квадратная таблица 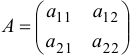 , составленная из четырёх чисел, называется квадратной матрицей 2-го порядка. Определителем 2-го порядка, соответствующим матрице
, составленная из четырёх чисел, называется квадратной матрицей 2-го порядка. Определителем 2-го порядка, соответствующим матрице  , называется число
, называется число
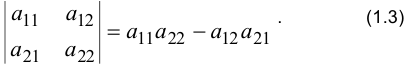
Аналогично, если 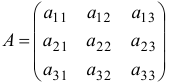
— квадратная матрица 3-го порядка, то соответствующим ей определителем 3-го порядка называется число
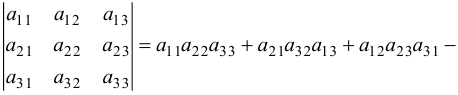
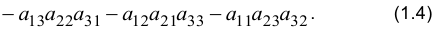
Например,

Числа 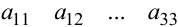 называют элементами определителя; первая цифра индекса указывает номер строки, в которой стоит элемент, вторая цифра индекса указывает номер столбца. Элементы
называют элементами определителя; первая цифра индекса указывает номер строки, в которой стоит элемент, вторая цифра индекса указывает номер столбца. Элементы 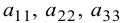 составляют главную диагональ определителя; элементы
составляют главную диагональ определителя; элементы 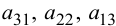 — вспомогательную диагональ.
— вспомогательную диагональ.
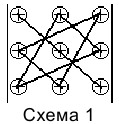
При вычислении определителя третьего порядка первые три слагаемые суммы снабжены знаком плюс и получены перемножением элементов, стоящих на главной диагонали и в вершинах треугольников, обозначенных на схеме 1.
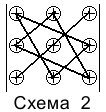
Слагаемые определителя, снабженные знаком минус, вычисляются перемножением элементов, стоящих на вспомогательной диагонали и в вершинах треугольников со стороной, параллельной вспомогательной диагонали (схема 2).
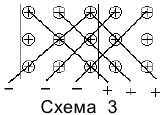
Определитель третьего порядка можно вычислить, если дописать к нему справа два его первых столбца, а затем перемножить элементы и сложить со знаками плюс или минус, как показано на схеме 3.
Свойства определителей (в справедливости указанных свойств определителей можно убедится проверкой).
1. Определитель равен нулю, если:
а) строка или столбец состоят из нулей;
б) имеется два одинаковых ряда (две строки или два столбца);
в) элементы параллельных рядов пропорциональны.
Например, пусть задан определитель с двумя одинаковыми столбцами:
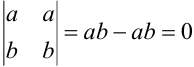 . Свойство справедливо.
. Свойство справедливо.
2. При умножении определителя на некоторое число 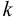 элементы одного ряда нужно умножить на это число:
элементы одного ряда нужно умножить на это число: 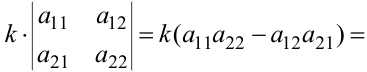
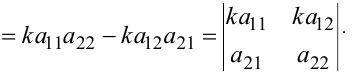
3. Определитель не изменится, если:
а) параллельные ряды поменять местами чётное число раз;
б) строки сделать столбцами, а столбцы — строками (такая операция называется транспонированием определителя):
в) к элементам одного ряда прибавить элементы другого ряда, умноженные на одно и то же число. Последнее свойство широко применяется при преобразованиях определителей с целью «обнуления» его элементов.
Например, задан определитель 
Умножим первую строку на (-2) и прибавим её ко второй строке. Затем умножим первую строку на (-3) и прибавим её к третьей строке. В результате получим определитель с тремя нулевыми элементами:
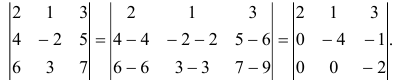
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
