Задача №106.
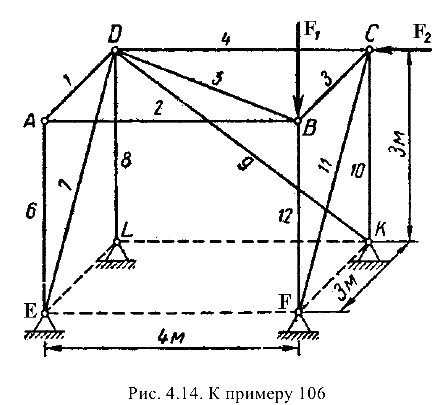
Определить усилия в стержнях пространственной фермы, изображенной на рис. 4.14, а также реакции опор фермы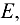 
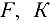и 
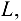если на узел 
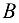фермы действует вертикальная сила 
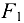= 50 кН, на узел 
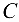— горизонтальная сила 
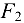= 25 кН, направленная вдоль стержня 
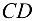. Размеры указаны на рисунке (рис. 4.14).
Решение:
Для определения усилий в стержнях 1-12 фермы воспользуемся способом вырезания узлов. Так как силы, действующие на каждый из узлов фермы, взаимно уравновешиваются, то, вырезая отдельные узлы фермы, составляем по три уравнения равновесия сил. действующих па каждый узел.
Узлы фермы вырезаем в такой последовательности, при которой число неизвестных сил в рассматриваемом узле не превышает трех. Так же, как и при определении усилий в стержнях плоских ферм, все стержни фермы условимся считать растянутыми; знак «минус» у вычисленной реакции стержня покажет, что стержень сжат.
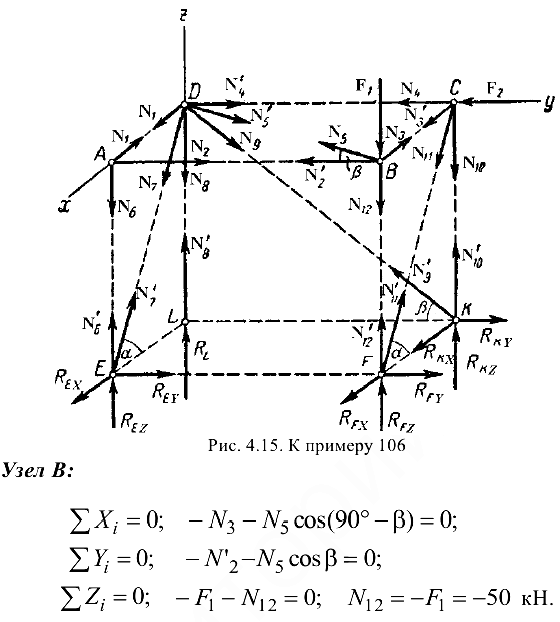
Для определения усилий в стержнях рассматриваемой фермы будем вырезать последовательно узлы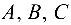 
и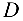 
(рис. 4.15).
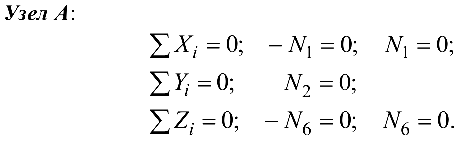
Так как узел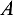 
не загружен внешней силой, а сходящиеся силы 
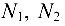и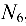 
не лежащие в одной плоскости, не могут уравновешиваться, то они равны пулю.
Из уравнения (4.22)
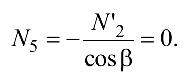
Из уравнения (4.21)
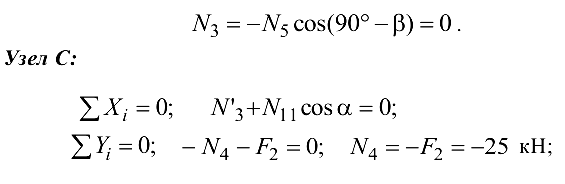
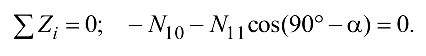
Из уравнения (4.23)
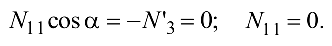
Из уравнения (4.24)
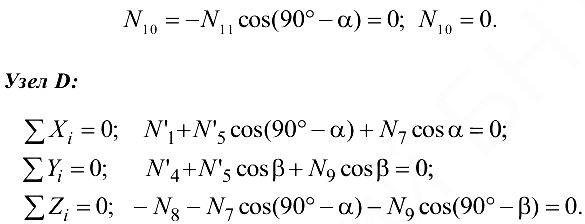
Найдем синусы и косинусы углов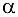 
и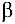 
. Так как
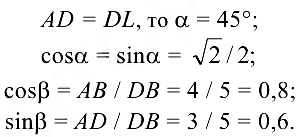
Из уравнения (4.25)
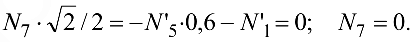
Из уравнения (4.26)
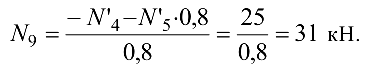
Из уравнения (4.27)
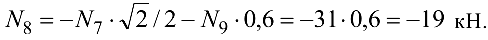
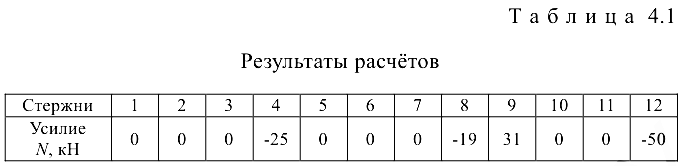
Основываясь на результатах расчета, можно установить следующее:
- Если в незагруженном узле фермы сходятся три стержня, не лежащие в одной плоскости, то усилия в каждом из этих стержней равны нулю (узел
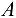, стержни 1, 2 и 6). - Если в некотором узле фермы все внешние силы и все стержни, кроме одного, лежат в одной плоскости, то усилие в стержне, не лежащем в этой плоскости, равно нулю (узел
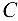, стержень 11 при 
).
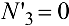Эти соображения, дающие возможность без вычислений определить стержни с нулевыми усилиями, значительно упрощают определение усилий в стержнях пространственных ферм.
Определив усилия в стержнях фермы способом вырезания узлов, можно определить реакции опор, представляющих собой шаровые шарниры. Реакцию каждой опоры неизвестного направления разложим на три составляющие, направленные вдоль осей координат. Эти составляющие определим из уравнений равновесия сил, приложенных к опорным узлам.
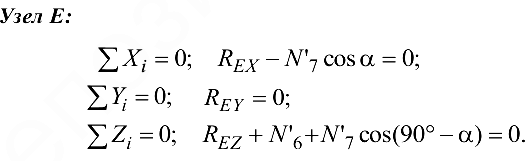
Из уравнения (4.28)
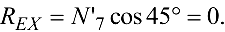
Из уравнения (4.29)
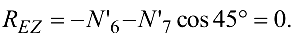
Так как
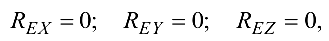
то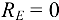 
, т.е. опора 
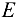не нагружена.
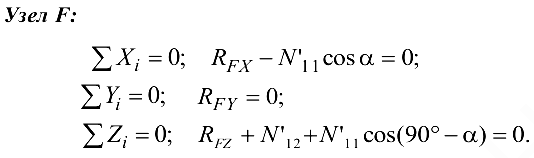
Из уравнения (4.30)
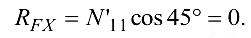
Из уравнения (4.31)
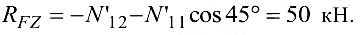
Знак «плюс» в ответе указывает на то, что истинное направление составляющей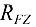 
совпадает с направлением, указанным на схеме.
Так как
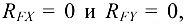
то реакция опоры направлена вертикально вверх и имеет модуль
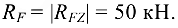
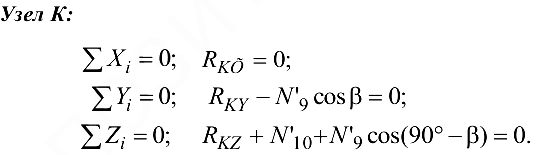
Из уравнения (4.32)
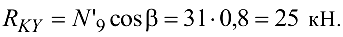
Из уравнения (4.33)
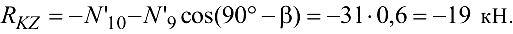
Знаки ответов показывают, что принятое направление силы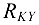 
совпадает с действительным, а силы 
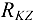— противоположно действительному (см. рис. 4.15).
Определим модуль и направление реакции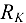 
:
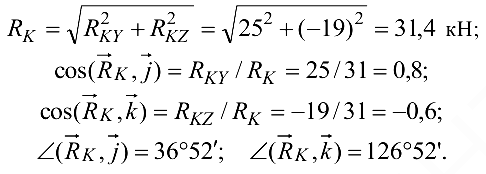
Узел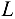 
:
Так как в узле 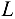неизвестна лишь реакция 
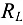, то составляем только одно уравнение:
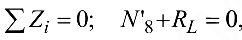
откуда
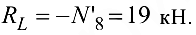
Знак «плюс» в ответе указывает на то, что реакция 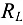направлена вертикально вверх.
Ответ:
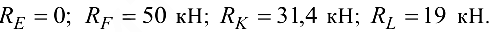
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:
