Задача №7.
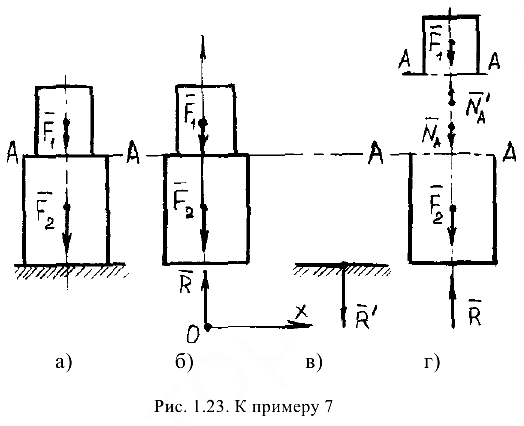
Определить силу давления ступенчатой колонны (рис. 1.23, а) на горизонтальную опору и силы взаимодействия частей колонны по сечению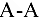 
. Сила тяжести (вес) верхней части колонны 
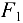= 30 кН, нижней 
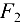= 60 кН.
Решение:
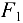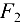По условию задачи надо рассмотреть равновесие колонны. Точки приложения сил и — в центре тяжести каждой части колонны. Действуют эти силы по одной вертикальной прямой -вниз, их модули заданы.
Опора колонны — горизонтальная плоскость, препятствующая ее перемещению по вертикали вниз. Действие опоры заменяем реакцией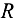 
, направленной вертикально вверх (рис. 1.23, б). Рассматриваемое тело находится в равновесии под действием трех сил, направленных по одной прямой. Для определения неизвестной силы реакции опоры применим уравнение равновесия.
Удобнее всего расположить оси координат таким образом, чтобы одна ось совпадала по направлению с силам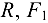и 
и 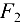, тогда получится одно уравнение равновесия (на ось 
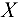все силы проецируются в точку):
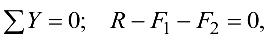
следовательно,
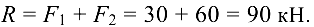
Сила давления колонны па опору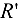 
(в соответствии с аксиомой о том, что действие равно противодействию) равна по модулю реакции 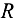, по направлена в противоположную ей сторону — вниз (рис. 1.23, в). Чтобы определить силы взаимодействия частей колонны по сечению 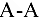, мысленно разделим обе части колонны и действие одной части па другую заменим силами, как показано па рис. 1.23, г.
Рассмотрим равновесие одной части колонны, например верхней:
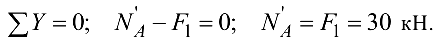
На основании аксиомы о равенстве действия и противодействия сила
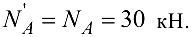
Тот же результат получится, если рассмотреть равновесие нижней части колонны:
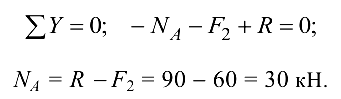
Ответ:
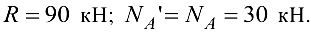
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:
