Оглавление:
Приступая к изучению этой темы, необходимо усвоить определение и основные свойства определенного интеграла.
При вычислении определенного интеграла используют формулу Ньютона — Лейбница
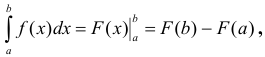
где 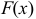 — любая первообразная функция
— любая первообразная функция 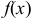 .
.
Методы вычисления определенных интегралов
1. Замена переменной осуществляется по формуле
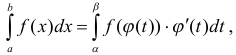
где 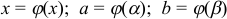 .
.
Эта формула справедлива, если 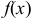 — непрерывная функция, а подстановка
— непрерывная функция, а подстановка 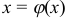 сама непрерывна на отрезке
сама непрерывна на отрезке 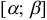 . Подчеркнем, что при вычислении определенного интеграла методом замены переменной, в отличие от неопределенного интеграла, возврат к старой переменной не требуется.
. Подчеркнем, что при вычислении определенного интеграла методом замены переменной, в отличие от неопределенного интеграла, возврат к старой переменной не требуется.
2. Интегрирование по частям
Если функции 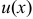 и
и 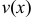 имеют непрерывные производные на
имеют непрерывные производные на 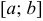 , то справедлива формула
, то справедлива формула
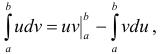
где символ 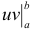 обозначает разность
обозначает разность 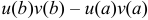 .
.
Приложения определенного интеграла
В этой теме предусмотрено применение определенного интеграла для вычисления площадей различных фигур, объемов тел вращения, длин кривых, работы и силы давления.
Вычисление площади в прямоугольных координатах
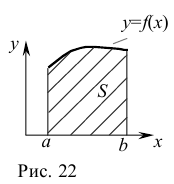
а) Если непрерывная кривая задана уравнением 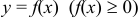 , то площадь криволинейной трапеции, ограниченной этой кривой, прямыми
, то площадь криволинейной трапеции, ограниченной этой кривой, прямыми 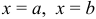
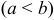 и осью
и осью 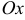 (рис. 22), вычисляется по формуле
(рис. 22), вычисляется по формуле
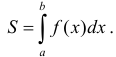
б) Если криволинейная трапеция ограничена непрерывными кривыми 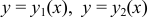 , причем
, причем 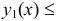
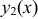 , и прямыми
, и прямыми 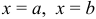
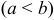 , то ее площадь вычисляется по формуле
, то ее площадь вычисляется по формуле 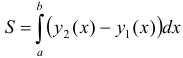 (рис. 23).
(рис. 23).
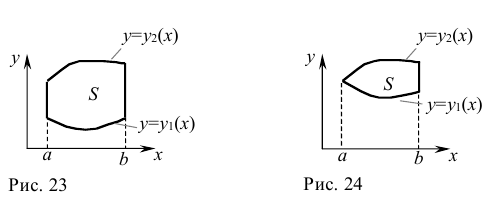
В отдельных случаях какая-либо граница 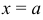 и
и 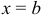 может выродиться в точку пересечения кривых
может выродиться в точку пересечения кривых 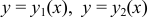 (рис. 24).
(рис. 24).
Параметрически заданная кривая 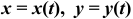
Площадь криволинейной трапеции, ограниченной этой кривой, двумя прямыми 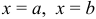
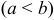 и осью
и осью 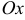 , выражается интегралом
, выражается интегралом
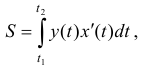
где 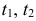 определяются из уравнений
определяются из уравнений 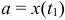 и
и 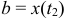 .
.
Вычисление площади в полярных координатах
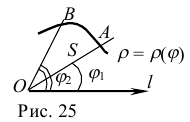
Если кривая задана уравнением в полярных координатах 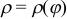 , то площадь криволинейного сектора
, то площадь криволинейного сектора 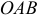 (рис. 25) вычисляется по формуле
(рис. 25) вычисляется по формуле
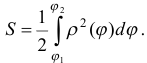
Объем тела вращения
Объем тела, образованного вращением вокруг оси 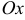 криволинейной трапеции, ограниченной кривой
криволинейной трапеции, ограниченной кривой 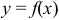 , осью
, осью 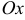 и прямыми
и прямыми 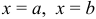 (см. рис. 22), вычисляется по формуле
(см. рис. 22), вычисляется по формуле 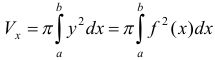 .
.
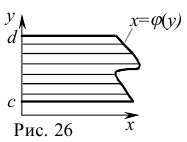
Объем тела, образованного вращением вокруг оси 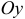 фигуры, ограниченной кривой
фигуры, ограниченной кривой 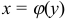 , осью ординат и прямыми
, осью ординат и прямыми 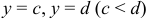 (рис. 26), вычисляются по формуле
(рис. 26), вычисляются по формуле
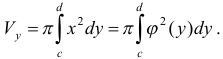
Если 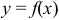 задана параметрическими уравнениями
задана параметрическими уравнениями 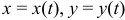 , то формула принимает вид
, то формула принимает вид
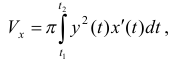
где 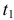 и
и 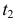 находятся из уравнений
находятся из уравнений 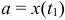 ,
, 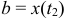 .
.
Длина плоских кривых
Если плоская кривая задана уравнением 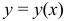 и производная
и производная 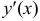 непрерывна, то длина дуги этой кривой выражается интегралом
непрерывна, то длина дуги этой кривой выражается интегралом
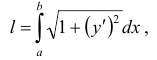
где 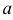 и
и 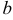 — абсциссы концов дуги.
— абсциссы концов дуги.
1. Если кривая задана уравнениями вида 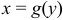 , то
, то
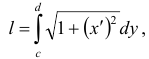
где 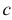 и
и 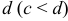 — ординаты концов дуги.
— ординаты концов дуги.
2. Если кривая задана в параметрической форме 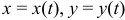 и производные
и производные 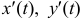 непрерывны на отрезке
непрерывны на отрезке 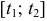 , то длина дуги кривой выражается интегралом
, то длина дуги кривой выражается интегралом
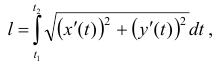
где 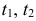 — значения параметра
— значения параметра 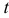 , соответствующие концам дуги
, соответствующие концам дуги 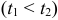 .
.
3. Если гладкая кривая задана уравнением 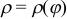 (см. рис. 25) в полярных координатах, то длина дуги
(см. рис. 25) в полярных координатах, то длина дуги 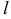 кривой выражается интегралом
кривой выражается интегралом
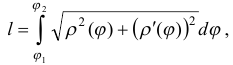
где 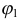 и
и 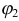 — значения полярного угла
— значения полярного угла 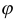 в концах дуги
в концах дуги 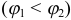 .
.
Физическое приложение
1) Общая схема применения определенного интеграла
Пусть требуется найти некоторую физическую величину 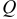 , имеющую определенное значение на отрезке
, имеющую определенное значение на отрезке 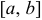 . Предполагается, что
. Предполагается, что 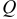 является аддитивной величиной, т. е. если отрезок
является аддитивной величиной, т. е. если отрезок 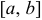 делится на части, то величина
делится на части, то величина 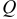 складывается из суммы значений
складывается из суммы значений 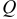 , соответствующих этим частям. Из условия задачи находят «элемент»
, соответствующих этим частям. Из условия задачи находят «элемент» 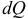 величины
величины 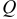 , отвечающий «элементарному» промежутку
, отвечающий «элементарному» промежутку 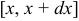 в виде
в виде 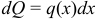 . После этого, интегрируя по отрезку
. После этого, интегрируя по отрезку 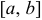 , получают величину
, получают величину 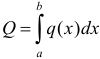 .
.
2) Путь, пройденный точкой.
Пусть точка движется по прямой с переменной скоростью 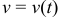 . Определить путь, пройденный точкой от момента времени
. Определить путь, пройденный точкой от момента времени 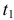 до момента
до момента 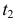 .
.
Решение:
За элементарный промежуток времени 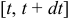 точка пройдет путь
точка пройдет путь
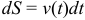 , где
, где 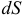 — «элемент пути» и
— «элемент пути» и 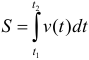 .
.
3)Работа силы.
Пусть материальная точка движется вдоль оси 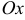 от точки
от точки 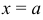 до точки
до точки 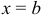
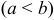 под действием переменной силы
под действием переменной силы 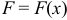 , причем направление силы совпадает с направлением движения. Найти работу, произведенную силой при этом перемещении.
, причем направление силы совпадает с направлением движения. Найти работу, произведенную силой при этом перемещении.
Решение:
На элементарном перемещении 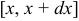 работа силы равна
работа силы равна 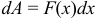 . Мы получили «элементарную» работу
. Мы получили «элементарную» работу 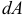 ,
, 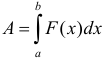 .
.
4) Сила давления жидкости на пластину выражается формулой
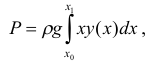
где 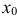 — глубина, на которой находится самая верхняя точка пластинки;
— глубина, на которой находится самая верхняя точка пластинки; 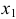 — глубина, на которой находится самая нижняя ее точка;
— глубина, на которой находится самая нижняя ее точка; 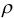 — удельная плотность жидкости;
— удельная плотность жидкости; 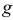 — ускорение свободного падения;
— ускорение свободного падения; 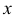 — расстояние точек пластинки до уровня жидкости;
— расстояние точек пластинки до уровня жидкости; 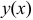 — длина горизонтального сечения пластинки (это неизвестная функция, зависящая от формы пластинки).
— длина горизонтального сечения пластинки (это неизвестная функция, зависящая от формы пластинки).
Пример 1.
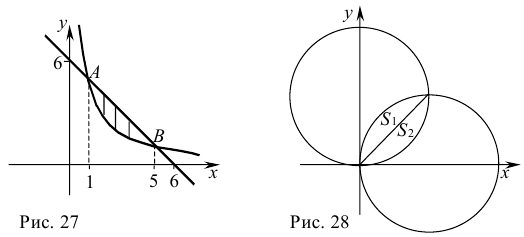
Вычислить площадь фигуры, заключенной между линиями
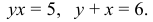
Решение:
Построим данную фигуру: 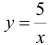 — гипербола,
— гипербола, 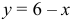 — прямая (рис. 27).
— прямая (рис. 27).
Найдем абсциссы точек пересечения прямой и гиперболы, решив систему уравнений 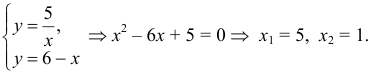
Искомая площадь равна:
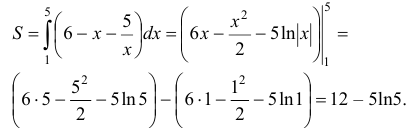
Ответ: 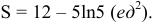
Пример 2.
Вычислить площадь фигуры, ограниченной линиями
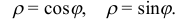
Решение:
Уравнения в полярных координатах 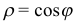 и
и 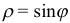 являются окружностями (рис. 28). Кривые, заданные в полярных координатах, можно строить по точкам с помощью ЭВМ. Основные кривые рассматриваются в предлагаемой литературе.
являются окружностями (рис. 28). Кривые, заданные в полярных координатах, можно строить по точкам с помощью ЭВМ. Основные кривые рассматриваются в предлагаемой литературе.
Очевидно, что 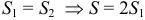 . Площадь криволинейного сектора можно найти по формуле
. Площадь криволинейного сектора можно найти по формуле 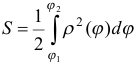 .
.
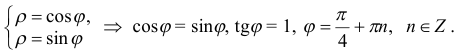
Уравнение луча 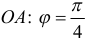 .
.
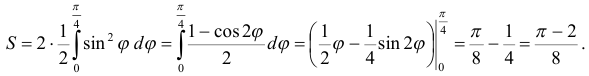
Ответ: 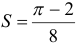 .
.
Пример 3.
Вычислить объем тела, полученного вращением вокруг оси 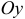 фигуры, ограниченной параболами
фигуры, ограниченной параболами 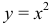 и
и 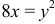 .
.
Решение:
Очевидно, что 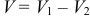 , где
, где 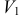 — объем тела, полученный вращением трапеции
— объем тела, полученный вращением трапеции 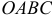 ,
, 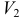 — объем тела, полученный вращением трапеции
— объем тела, полученный вращением трапеции  (рис. 29).
(рис. 29).
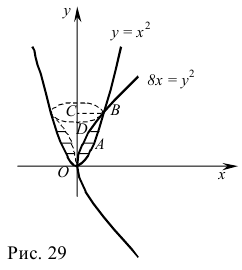
Найдем ординаты точек пересечения парабол:
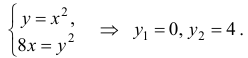
Уравнение параболы 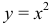 (кривая
(кривая 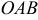 ) запишем в виде
) запишем в виде 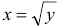 , тогда
, тогда
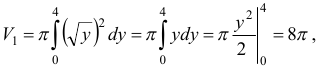
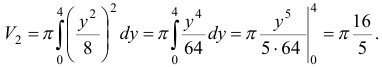
Следовательно, 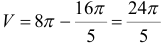 .
.
Ответ: 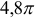 .
.
Пример 4.
Вычислить объем тела, которое получается от вращения фигуры, ограниченной кардиоидой 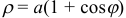 вокруг полярной оси.
вокруг полярной оси.
Решение:
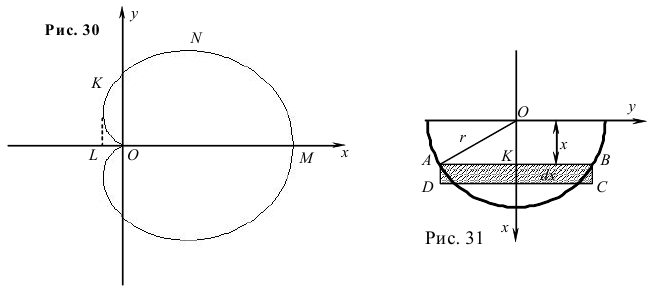
Искомый объем представляет собой разность объемов, получаемых от вращения вокруг оси 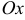 (она же и полярная ось) фигуры
(она же и полярная ось) фигуры 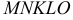 и
и 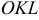 (рис. 30).
(рис. 30).
Перейдем к параметрическому заданию кривой, приняв за параметр полярный угол 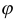 :
: 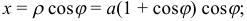
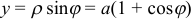
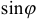 .
.
Очевидно, что абсцисса точки 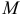 равна
равна 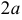 (значение
(значение 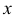 при
при 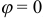 ). Абсцисса точки
). Абсцисса точки 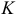 есть значение минимума функции
есть значение минимума функции 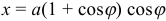 .
.
Найдем этот минимум: 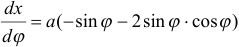 ,
, 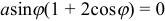 ,
, 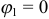 и
и 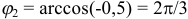 . При
. При 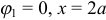 , при
, при 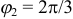 получаем
получаем 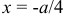 .
.
Координаты точки 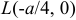 . Следовательно, искомый объем
. Следовательно, искомый объем
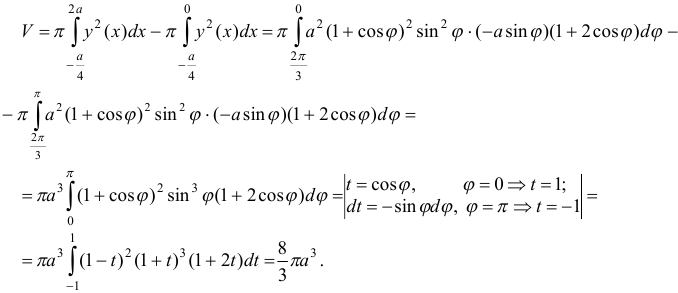
Ответ: 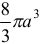 .
.
Пример 5.
Найти силу давления, испытываемую пластиной с одной стороны в форме полукруга радиуса 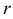 , погруженного в жидкость так, что диаметр совпадает с поверхностью жидкости.
, погруженного в жидкость так, что диаметр совпадает с поверхностью жидкости.
Решение:
Вычислим силу давления, испытываемую «элементом» пластины 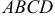 на глубине
на глубине 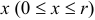 :
:
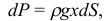
где 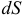 — площадь элемента пластины
— площадь элемента пластины 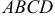 (рис. 31),
(рис. 31), 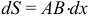 .
.
Из 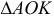 по теореме Пифагора находим:
по теореме Пифагора находим:
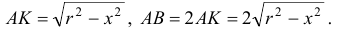
Тогда 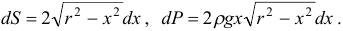
Вычислим силу давления на пластину:
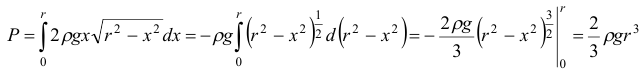
Ответ: 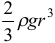 .
.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:

