Определение производной функции
Пусть функция 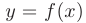 определена на некотором интервале значений аргумента
определена на некотором интервале значений аргумента 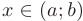 . Дадим аргументу
. Дадим аргументу 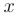 приращение
приращение 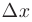 такое, что
такое, что 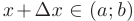 и найдем соответствующее приращение функции:
и найдем соответствующее приращение функции:
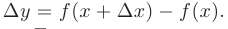
Если существует предел отношения приращения функции 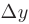 к приращению аргумента
к приращению аргумента 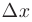 , при произвольном стремлении последнего к нулю
, при произвольном стремлении последнего к нулю
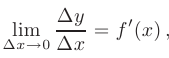
то он называется производной функции 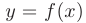 в точке
в точке 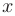 и обозначается как:
и обозначается как:
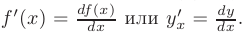
Если функция 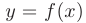 имеет в некоторой точке
имеет в некоторой точке 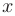 производную, то говорят, что функция дифференцируема в этой точке. Заметим, что дифференцируемость функции
производную, то говорят, что функция дифференцируема в этой точке. Заметим, что дифференцируемость функции 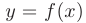 в точке
в точке 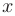 является достаточным условием для ее непрерывности в этой же точке, в то время как обратное утверждение, вообще говоря, неверно. Например, функция
является достаточным условием для ее непрерывности в этой же точке, в то время как обратное утверждение, вообще говоря, неверно. Например, функция 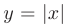 непрерывна в точке
непрерывна в точке 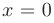 , но не дифференцируема в ней.
, но не дифференцируема в ней.
Геометрический смысл производной. Производная функции 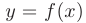 в точке
в точке 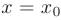 равна угловому коэффициенту касательной, проведенной к графику функции в данной точке:
равна угловому коэффициенту касательной, проведенной к графику функции в данной точке:
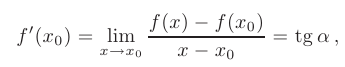
где 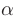 — угол наклона касательной к графику функции в данной точке.
— угол наклона касательной к графику функции в данной точке.
Тогда уравнение касательной к графику функции 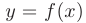 в точке
в точке 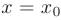 будет иметь вид
будет иметь вид
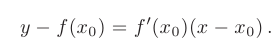
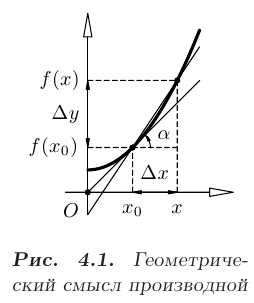
Пример взаимного расположения секущей и касательной к графику функции 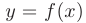 в точке
в точке 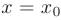 показан на рис. 4.1.
показан на рис. 4.1.
Экономический смысл производной. Предположим, что известна зависимость издержек производства 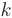 однородной продукции от ее количества
однородной продукции от ее количества 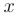 . Приращению количества производимой продукции
. Приращению количества производимой продукции 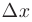 соответствует приращение издержек производства
соответствует приращение издержек производства 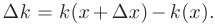 . Среднее приращение издержек производства характеризуется отношением
. Среднее приращение издержек производства характеризуется отношением 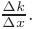 Тогда, если существует предел этого отношения
Тогда, если существует предел этого отношения
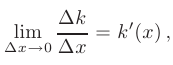
то его называют предельными издержками производства. С помощью понятия производной в экономике характеризуют и другие предельные понятия.
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Непрерывность функции в математике |
| Асимптоты графика функции в математике |
| Производные основных элементарных функций в математике |
| Дифференциал функции в математике |

