Определение перемещений методом Максвелла-Мора
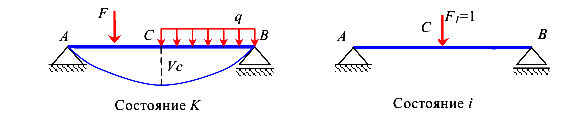
Рассмотрим балку, загруженную нагрузкой общего вида -сосредоточенными моментами, силами и равномерно распределенными нагрузками. Обозначим это состояние балки состоянием k.
Рассмотрим эту же балку, загруженную единичной силой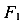 
= 1, приложенной в произвольной точке. Обозначим такое состояние балки i.
Пусть требуется определить перемещение точки, к которой приложена единичная сила (99).
Работа внешних сил
Работа внутренних сил
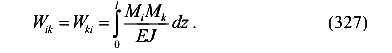
Учитываем закон сохранения энергии
и получим
Запишем в общем виде
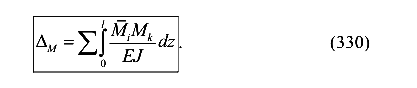
Полученное выражение называется интегралом Мора.
Здесь
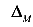— линейное или угловое перемещение, вызванное изгибом балки;-
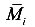— функция изгибающего момента, вызванная единичной силой (черточка вверху означает, что эта величина от единичной силы); -
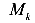— функция изгибающего момента от нагрузки; - l — длина участков балки.
Интеграл берется на каждом участке отдельно, а затем все интегралы суммируются.
Аналогично для стержня, подвергнутого центральному растяжению-сжатию
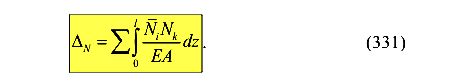
Деформации стержня от сдвига
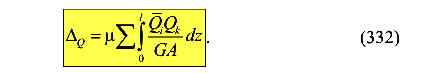
Здесь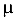 
— коэффициент, зависящий от формы сечения (по справочнику) Деформации стержня от кручения
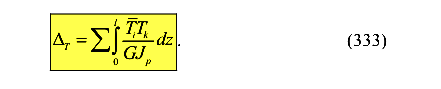
Таким образом, полная форма имеет вид
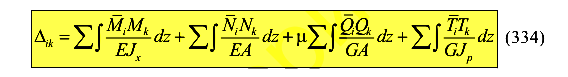
В сечениях балки, испытывающей поперечный изгиб, продольные силы и крутящие моменты равны нулю N = 0, Т = 0. Влиянием поперечных сил на деформации балки пренебрегают. Поэтому, обычно, для балок используется только первый интеграл.
Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Решение задач по сопротивлению материалов
Дополнительные страницы которые вам будут полезны:
| Теорема о взаимности работ внутренних сил |
| Теорема о взаимности перемещений |
| Вычисление интеграла Мора способом Верещагина |
| Разложение эпюр на составляющие треугольной и параболической форм |
